利用幾何直觀　揭示數學規律
——“釘子板上的多邊形”教學片斷及思考

江蘇泰州市姜堰區東橋中心小學（225500）　翟紅梅

?

利用幾何直觀揭示數學規律
——“釘子板上的多邊形”教學片斷及思考

江蘇泰州市姜堰區東橋中心小學（225500）翟紅梅

幾何直觀憑借圖形的直觀性特點，將抽象的數學語言與直觀的圖形語言有機地結合起來，即把抽象思維與形象思維相結合，能夠充分揭示問題的本質，激活學生的思維。學生經歷充分探索規律的過程，根據自己的興趣自主畫圖、計算、驗證、分類歸納，抽象概括出研究事物的共同特征，從而揭示釘子板上多邊形蘊含的秘密，對規律本質的認識逐漸深入、完善。

直觀感知幾何直觀數學規律抽象概括合作探究

《數學課程標準》指出：“幾何直觀主要是利用圖形描述和分析問題。借助幾何直觀，可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路。”“釘子板上的多邊形”是蘇教版小學數學五年級上冊的內容，課堂教學中，如何引導學生利用幾何直觀探索規律，掌握解決問題的方法，積累數學活動經驗呢？對此，我進行實踐和思考。

教學片斷一：直觀感知，引發沖突

1.獨立研究

2.匯報結果

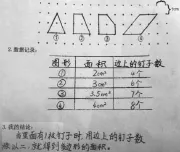
生1：我研究的是這些多邊形的面積和邊上釘子數的關系，發現這里多邊形的面積都等于邊上的釘子數除以2。

生2：我覺得用文字表達不太清楚。

生3：可以用字母來表示，這樣簡潔些。如用n表示多邊形邊上的釘子數，用S表示多邊形的面積，那發現的規律就可以表示為S=n÷2。

3.思考質疑

師：是不是釘子板上每個多邊形的面積和它邊上的釘子數都有這樣的關系呢？

4.分析驗證

學生選擇之前自己任意圍出的多邊形數一數、算一算，看看它們的面積與邊上的釘子數是不是也有這樣的關系。

5.交流討論

生4：我圍出的多邊形面積和邊上的釘子數不符合這個規律，因為我的圖形內部是3顆釘子。

生5：我圍出的多圖形面積和邊上的釘子數也不符合這個規律，因為我的圖形內部是2顆釘子。

生6：這里多邊形的面積等于邊上的釘子數除以2，需要添加一個條件，那就是“當多邊形內部釘子數為1時”。由于我的同桌研究多邊形內部的釘子數不是1，所以就沒有這樣的規律。

6.抽象概括

師：如果用a表示多邊形內部的釘子數，那么當a=1時，S=n÷2。

7.梳理總結

師：剛剛我們是怎樣研究出多邊形的面積和邊上釘子數的關系的？

生7：我們是通過“觀察圖形——分析數據——得出結論——舉例驗證”的過程進行研究的。

……

思考：

上述教學，先讓學生進行獨立操作，再小組交流，引導學生探索多邊形內部的釘子數為1的情況。學生通過研究單上的一組組數據發現規律，初步得出結論，從而獲得探究成功的滿足感。我再提出問題：“是不是釘子板上每個多邊形的面積和它邊上的釘子數都有這樣的關系？”學生再次通過動手操作，驗證自己圍出的多邊形是否具有這樣的規律。這里由特殊到一般，幾何直觀憑借圖形的直觀性特點，將抽象的數學語言與直觀的圖形語言有機地結合起來，即把抽象思維與形象思維相結合，充分揭示了問題的本質，激活了學生的思維。接著，我引導學生從自己圍出的圖形開始研究，充分體現了學生學習的自主性和趣味性。這樣不僅讓學生發現了規律，更重要的是讓學生經歷了探索規律的過程，學會了研究的基本方法，積累了數學活動經驗，為后續的研究活動做好了準備。

教學片斷二：開放研究，提升認識

1.提出問題

師：同學們每人都任意圍了一個多邊形，是不是該研究自己的圖形了？只有一個圖形可以研究嗎？為什么？怎么辦？

生1：一個圖形不便于找出規律，我提議我們根據圍出的多邊形內部釘子的顆數重新分組，可以分成內部沒有釘子的，或有2顆、3顆、4顆……釘子的。

2.合作探索

學生小組內操作、填表、比較、歸納。

3.交流收獲

生2：我們小組研究的是圖形內部有2顆釘子的情況，我們得出“（外部的釘子數+內部的釘子數）÷2=圖形的面積”，用字母表示為S=（n+2）÷2。

師：這里多邊形的面積不等于n÷2，那它和n÷2有關系嗎？同桌互相討論，看看有什么發現。

生3：我們可以將S=（n+2）÷2=n÷2+ 1進行計算。

生4：前面還要加上“當多邊形內部釘子數a=2時”。（師板書：a=2時，S=n÷ 2+1）

生5：我們小組研究的是圖形內部有3顆釘子的情況，我們得出a=3時，S=n÷2+2。

生6：我們小組研究的是圖形內部沒有釘子的情況，我們得出a=0時，S=n÷2-1。

……

思考：

在初探規律后，學生產生認知沖突，發現圖形內有2顆釘子時，規律并不和圖形內有1顆釘子的一樣。這樣激發了學生繼續探究的欲望，自主設計圖形并探索其中的規律，從而完善第一次的認知。學生由圖形內有1顆釘子的多邊形面積與釘子數的關系，進一步探索多邊形內有2顆釘子、3顆釘子、0顆釘子時多邊形面積與邊上釘子數的關系。在這次活動中，學生利用得到的認知規律進行猜想，并根據自己的興趣自主畫圖、計算、驗證，從而揭示釘子板上圖形的秘密，使最初的感知更加深入、更加具體，對規律本質的認識逐漸完善。這里，我對學生探索的問題采取開放分類研究的方式，滿足了不同學生的不同需求，最大限度地促進學生的發展，讓學生體驗到探究成功的樂趣。

在這次實踐活動中，我以圖形為紐帶，利用幾何直觀讓學生經歷充分探索的過程，體驗研究的方法，從而揭示多邊形面積與邊上的釘子數之間的關系，培養了學生積極主動借助幾何直觀去發現問題、解決問題、揭示規律的能力。

（責編藍天）

G623.5

A

1007-9068（2016）20-038