一道填空題的高零分率引發的思考的再思考

浙江省德清縣三合中心學校　沈國

一道填空題的高零分率引發的思考的再思考

原題:如圖1,在平面直角坐標系xOy中,已知正三角形ABC的邊長為2,點A從點O開始沿x軸的正方向移動,點B在∠xOy的平分線上移動,則點C到原點O的最大距離是_________.

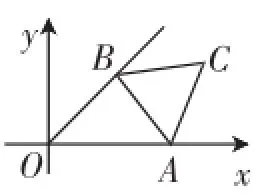
圖1

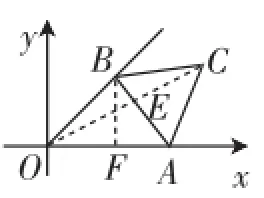
圖2

在文1中朱玉祥老師重點分析了該題的高零分率的原因,主要探究了該題的命題者是怎樣一步步賦予它如此高的難度.朱老師從該題的"源頭"梯子滑動問題開始,到變換角度求△AOB的最大面積,再到求一個頂點與原點的最大距離,最后變換到A、B兩動點放在銳角的兩邊上滑動,清晰地展現了該題是如何一步一步變化過來的,難度是如何一點點上升的.筆者閱讀之后受益匪淺,十分贊同朱老師的觀點,作為一道填空題的壓軸題,學生如果沒有經歷過這樣一個試題改編的過程,不借助"梯子"是很難一步跨越的.

文1中原題的答案如下所示.

如圖2,連接OC,交AB于E,當OC⊥AB時,OC有最大值(理由如題3).此時OC也平分AB,且∠ACE=30°.

設OA=OB=x,作BF⊥OA,垂足為F.

在Rt△BOF中,因為∠BOF=45°,所以BF=OB.sin45° =xX.在Rt△AFB中,因為AF2+BF2=AB2,所以

文1中的題3及其解題思路如下所示.

(2009.山東)如圖3,已知邊長為a的正三角形ABC,兩頂點A、B分別在平面直角坐標系的x軸、y軸的正半軸上滑動,點C在第一象限,連接OC,則OC的長的最大值是_________.

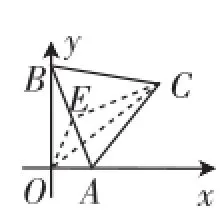
圖3

連接OC,取AB的中點E,連接CE、OE,如圖3,顯然OC≤OE+CE,而OE與CE的和是個定量,所以當A、B在滑動中使OC經過點E,也就是OC=OE+CE時,OC的長度最大.此時,△AOB為等腰直角三角形(面積最大),所以,而△ABC是等邊三角形,AB=a,所以OC的最大值為

筆者閱讀完原題的答案及題3的解題過程后,對原題答案中的"當OC⊥AB時,OC有最大值(理由如題3)"這句話產生了幾點疑問.

疑問一:當OC⊥AB時,OC是否最大?

疑問二:"理由如題3",這樣說理學生能接受嗎?這兩道題是屬于本質相同的問題嗎?

疑問三:有沒有更好的方法,有沒有能讓學生接受并可以理解的方法?

筆者對這三個疑問的思考如下所示.

對于疑問一,筆者好像無法根據題3的解題思路來證明,只能借助幾何畫板來證實當OC⊥AB時OC確實最大(如圖4).

OC=4.07611厘米OC=4.13981厘米OC=4.09916厘米

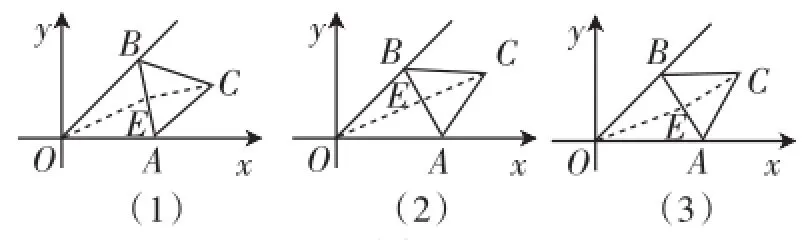
圖4

對于疑問二,筆者認為題3的說理過程學生能理解,也能接受,因為依據的是三角形三邊的關系,即三角形中兩邊之和大于第三邊,但是能否用此來作為原題中OC取得最大值的依據,筆者認為值得商榷.題3中OC≤OE+CE,且OE與CE都是定值,當O、C、E三點共線時OC最大.而原題中(如圖5),OC≤OE+CE,但OE是個變量,為什么三點共線時OC最大呢?對于這點,朱老師好像沒解釋清楚,只是說題3中OC取得最大值時△AOB為等腰直角三角形(面積最大),然后朱老師就認為原題中OC取得最大值時△AOB也為等腰三角形.筆者認為這樣說理不科學,依據的是一種解題經驗,而不是真正意義上說理的依據.這里學生即便做過題3,且能找到OC最大時的位置,如果讓他馬上做原題,我相信絕大部分學生還是束手無策,即使能做對也是猜對了OC取得最大值時的位置,至于為什么此時OC最大他也說不清楚.

那么這兩道題的本質是否相同?應該說原題是題3的一個變式,題3是一種特殊情況,原題是一般情況,但是這種變式已經改變了點E運動的軌跡,題3中點E運動的路徑是圓弧(如圖6),而原題中點E運動的路徑則是橢圓(如圖7),雖然圓是橢圓的一種特殊情況,但是在這里當OC取得最大值時用同樣的說理過程好像不夠嚴密.可能朱老師站的角度還要高,能一下子就洞察到這兩種情況的本質是一樣的,但是我們又該如何面對我們的學生呢?接下來就是筆者對疑問三的思考.

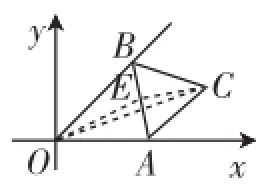
圖5

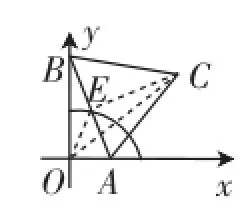
圖6

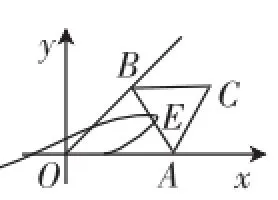
圖7

題3是抓住了AB的中點E找到了解題的突破口,利用同樣的方法來解決原題則不行,既然兩道題是屬于本質相同的題目,那么這兩題肯定有相通的地方.筆者注意到雖然原題做了適當的改編,但是也有相同的地方,即兩道題中AB的長是定值,以及在邊AB運動的過程中其所對的角度也都一直沒變,這樣筆者就想到了可以通過構造輔助圓來解決原題.因為我們知道,當一個三角形的一邊長不變,其所對角度也一定時,這個三角形的外接圓的半徑是不變的.這樣解決原題就更簡單了,如圖8,構造△AOB的外接圓⊙H,因為圓周角∠AOB=45°,所以圓心角∠AHB=90°.因為AB=2,所以AH= BH=.連接CH交AB于E,進一步可得CH⊥AB于E,所以EH=1,CE=,所以CH=1+.因為OC≤OH+CH,而OH與CH的和是個定值,所以當O、H、C三點共線時,OC的長度最大,即OC=OH+CH=1++.

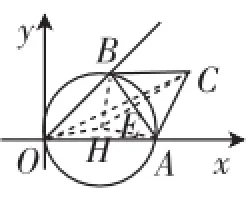
圖8

對于這種方法,學生只要能理解⊙H的大小不變,后面的解題過程理解起來應該沒問題.這種解法跟題3的解法是一樣的,這種方法才是這兩道題的通法,只不過題3中,點E和△AOB的外心是互相重合的,且點E又剛好是AB的中點,由于思維的定勢,做原題時學生也會先去找AB的中點,由于OE的長是變化的,所以就沒法往下做了,阻斷了學生的思路.題3中可以根據直角三角形斜邊上的中線等于斜邊的一半確定OE的長不變,沒有必要畫出輔助圓,所以做原題時學生沒有這方面的經驗,也就想不到要構造輔助圓,從而就不能像題3一樣將OC的長轉化成小于或等于兩條固定線段長度之和,就找不到解決問題的突破口,正是由于這些原因,才真正導致原題這么高的零分率吧.根本原因是學生對于構造輔助圓的問題不夠熟練,所以我們在平時教學中,還是應該讓學生多關注一下這類題目,如下面的兩道很有新意的題目.

題目1:(2010.德清縣自主招生)今有一副三角板(如圖9),中間各有一個直徑為4cm的圓洞,現將三角板a的30°角的那一頭插入三角板b的圓洞內(如圖10),則三角板a通過三角板b的圓洞的那一部分的最大面積為_________cm2.(不計三角板的厚度,精確到0.1cm2)

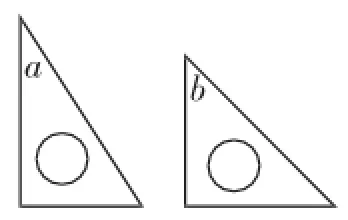
圖9

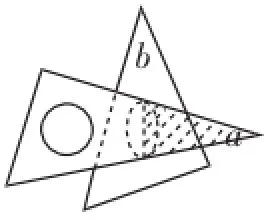
圖10

題目2:(2014.武漢模擬)如圖11,在⊙O中,弦AD等于半徑,B為優弧AD上的一動點,等腰△ABC的底邊BC所在直線經過點D.若⊙O的半徑等于1,則OC的長不可能為().

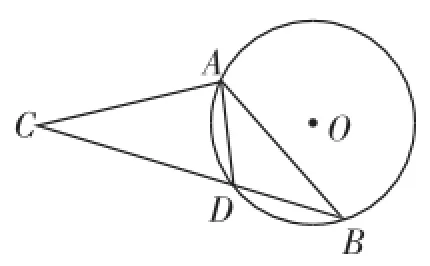
圖11

總之,在教學中,我們要引導學生用數學的眼光去審視問題、探究問題,高度把握數學題的本質.在學生認知和技能的最近發展區的基礎上,通過變式、類比對習題進行再研究,尋求問題的增長點,從而達到做一題、會一類、通一片.同時我們也要關注學生分析問題的思路,關注推理的嚴謹性,關注合理表述、規范書寫,從而提高教學的有效性及針對性.

1.朱玉祥.一道填空題的高零分率引發的思考[J].中學數學教學參考(中),2014(4).

2.朱松林.變式延伸從最近發展區開始[J].中學數學(下),2013(1).

3.楊紹平.貴有解題思路重在推理嚴謹---南京市2013年中考數學第25題評析[J].中學數學(下), 2013(9).