淺析中考中的三大類特殊圖形旋轉問題歸類剖析

江蘇省張家港市第二中學　陳曉芳

淺析中考中的三大類特殊圖形旋轉問題歸類剖析

中學階段涉及三種基本的全等變換,分別是平移、旋轉和翻折.這些全等變換具有如下的基本特征和解決思路:圖形在變換前后的基本性質不變,分析這些圖形變換時,對給定的圖形進行某種位置變化以后,在變化過后的圖形中分析有關圖形之間的對應關系.這類問題的共同特點是:考查該知識與其他知識之間的聯系,解題靈活多變,注重考查學生分析問題和解決問題的能力;結論也相對開放,注重考查學生的推理、猜想、探索能力.

對于三種基本的全等變化,以旋轉變換考查的力度最強,出現的相關試題也最多.根據旋轉的定義:在平面內,將一個圖形繞一個定點沿某個方向轉動一個角度成為與原來相等的圖形叫做圖形的旋轉,這個定點叫做旋轉中心,圖形轉動的角稱為旋轉角.圖形旋轉時,圖形中的每一點旋轉的角都相等,都等于圖形的旋轉角.下面就來剖析一下中考中的旋轉類問題的幾種基本考試模型.

一、正三角形類型

在等邊△ABC中,P為三角形內一點,將△ABP繞A點按逆時針方向旋轉60°后得到AB與AC重合.通過以上的變化過程,將圖1中的PA、PB、PC三條線段變化成圖2中的一個△P′CP中,此時△P′AP也應該為等邊三角形(正三角形).

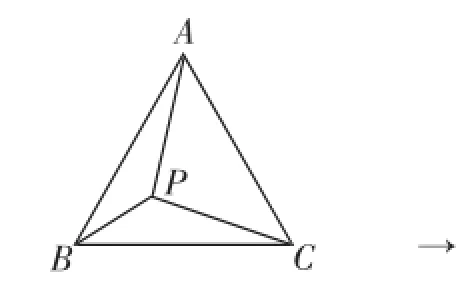
圖1

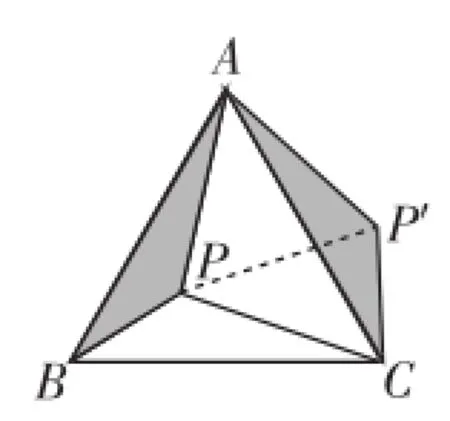
圖2

二、正方形類型

在正方形ABCD中,P為正方形ABCD內一點,將△ABP繞B點按順時針方向旋轉90°,使得BA與BC重合.經過如下變化:將圖3中的PA、PB、PC三條線段變化成圖4中的△CPP′中,此時可以得到等腰直角三角形△BPP′.

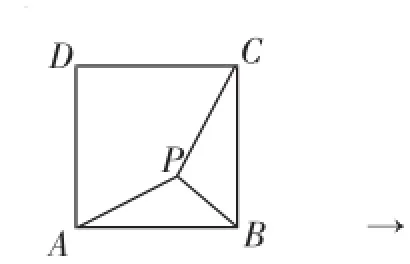
圖3

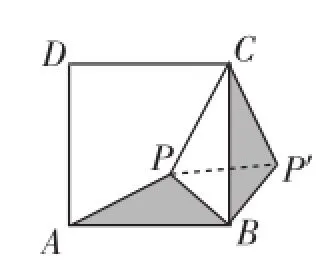
圖4

三、等腰直角三角形類型

如圖5,在等腰直角三角形△ABC中,∠C=90°,P為△ABC內一點,將△APC繞C點按逆時針方向旋轉90°,使得AC與BC重合.經過這樣旋轉變化,在圖6中的一個△P′CP為等腰直角三角形.

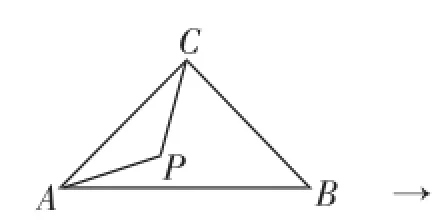
圖5

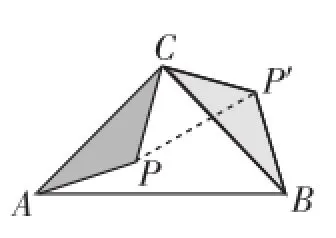
圖6

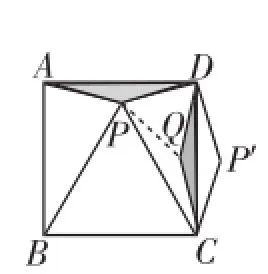
圖7

例1如圖7,正方形ABCD內有一點P,∠PAD=∠PDA=15°,連接PB、PC,請問:△PBC是等邊三角形嗎?為什么?

解析:解決問題的關鍵是得出∠PCD=∠PBA=30°,由前面的分析過程可得,如果將△APD繞點D逆時針方向旋轉90°,使A與C重合,這個問題就得到很好的解決了.由此可知,旋轉變化作為幾何變換中的最常見的變換情況,它一般先會對給定的圖形進行相應的旋轉變化,通過改變位置產生新的情況,然后在新出現的圖形中分析相關圖形之間的內在聯系,從而揭示出解決問題的一般方法,最終完美地解決問題.

例2(2015年黑龍江省齊齊哈爾市)如圖8,在正方形CGEF和正方形ABCD中,點B、C、G在同一條直線上,AE的中點為M,延長DM交EF于點N,連接FM,可得DM= FM,DM⊥FM(證明過程不必書寫).

(1)在圖9中,當點B、C、F在同一條直線上時,延長DM交EG于點N,其余條件不變,請你思考一下線段FM與DM存在怎樣的數量關系和位置關系?寫出猜想,并進行證明.

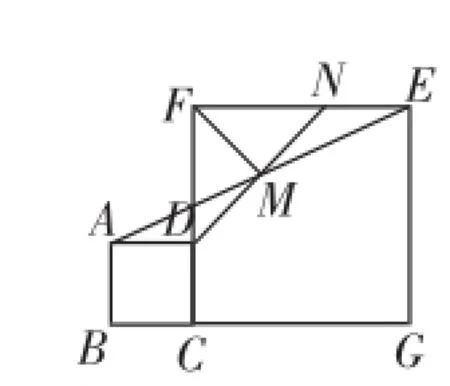
圖8

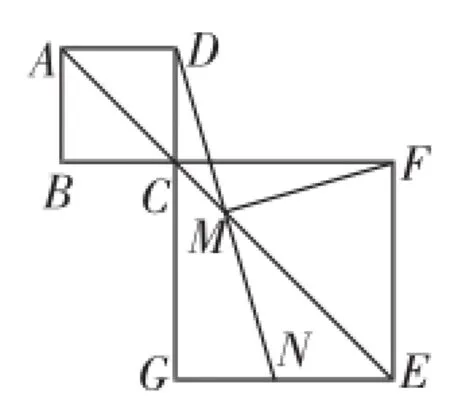
圖9

(2)在圖10中,當點E、B、C在同一條直線上時,延長DM交CE的延長線于點N,不改變其他條件,探究線段DM與FM有怎樣的關系?直接寫出你的猜想.

分析:本題考查了圖形的證明,涉及正方形的性質、三角形全等的判定及性質,解題的關鍵是通過構造全等三角形,實現線段的轉化及等腰三角形三線合一性質的應用.可以先證明△MAD≌△AEN,得到DM=MN;再證明△DCF≌△NEF,得到DF=FN,應用等腰三角形三線合一的性質得到DM⊥FM.

解:(1)在圖9中,關系為DM=FM,DM⊥FM.

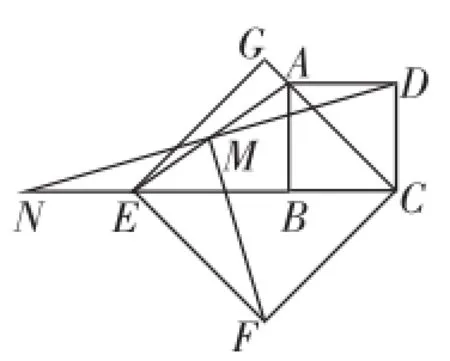
圖10

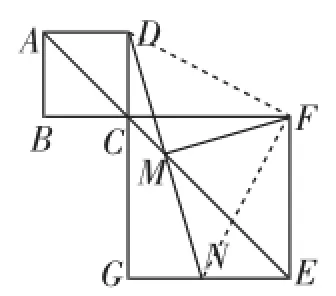
圖11

證明如下:如圖11,連接DF、NF.

因為四邊形ABCD和四邊形CGEF都是正方形,

所以AD∥BC,BC∥GE,所以AD∥GE,

所以∠DAM=∠NEM.

因為M是AE的中點,所以AM=EM.

因為∠AMD=∠EMN,所以△MAD≌△MEN.

所以DM=MN,AD=NE.

因為AD=CD,所以CD=NE.

因為CF=EF,∠FCD=∠FEN=90°,

所以△DCF≌△NEF.

所以DF=FN,∠CFD=∠EFN.

因為∠EFN+∠CFN=90°,

所以∠CFD+∠CFN=90°,即∠DFN=90°.

所以DM=FM,DM⊥FM.

(2)圖12中,連接DF、NF、MF.

因為四邊形ABCD是正方形,所以AD∥BC.

所以∠ADM=∠ENM.

因為M是AE的中點,

所以AM=EM.

因為∠AMD=∠EMN,

所以△MAD≌△MEN.

所以DM=MN,AD=NE.

因為AD=CD,所以CD=NE.

因為∠FCD=∠DCB+∠BCF=90°+45°=135°,

∠FEN=180°-∠BEF=180°-45°=135°,

所以∠FCD=∠FEN.

因為CF=EF,所以△DCF≌△NEF.

所以DF=FN,∠CFD=∠EFN.

因為∠EFD+∠CFD=90°.

所以∠EFN+∠CFD=90°,即∠DFN=90°.

所以△FND為等腰直角三角形.

因為MN=MD,所以DM=FM,DM⊥FM.

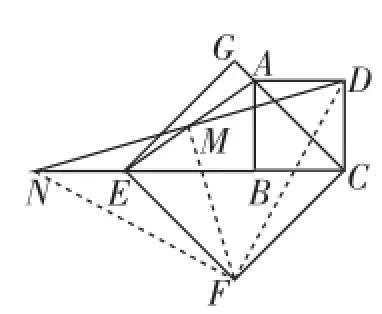
圖12

通過以上中考實例的解答,再聯系一下圖形的旋轉思想,是否有更為簡單的做法呢?不妨動手試一試.通過這個中考實例,可以看到旋轉變化的本質就是抓住變化前后的不變性給予解決.