推陳出新求簡潔，自然生長思關聯

☉江蘇省海安縣城南實驗中學劉東升

推陳出新求簡潔，自然生長思關聯

☉江蘇省海安縣城南實驗中學劉東升

在近期教學實踐中，筆者將一些敘述較為繁冗的“陳題”（這里的“陳題”是指在各級考題中反復出現，且在網絡上百度一些關鍵詞后很快會出現大量這樣的雷同題），本著追求簡潔的命題取向，將其改編后提供給學生練習，取得較好的訓練效果.本文選取三個陳題改編的題例，并附改編意圖與命題思考，提供研討.

一、陳題與改編的題例呈現

陳題1探究題：如圖1.

（1）△ABC為等邊三角形，動點D在邊CA上，動點P在邊BC上，若這兩點分別從點C、B同時出發，以相同的速度由C向A和由B向C運動，連接AP、BD交于點Q，求證：AP=BD；

（2）如果把原題中的“動點D在邊CA上，動點P邊BC上”，改為……，其他條件不變，請你利用圖2的情形，求證：∠BQP=60°；

（3）如果把原題中的“動點P在邊BC上”，改為……，如圖3，則動點D、P在運動過程中，求證：DE=PE.

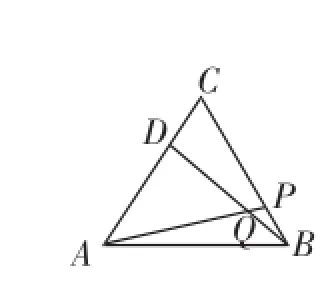
圖1

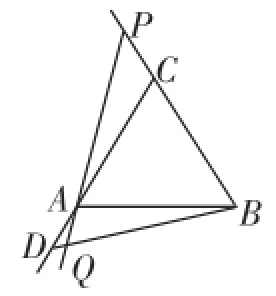
圖2

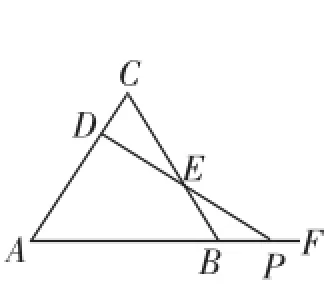
圖3

簡評：該題陳述繁冗，表述不清，極容易造成誤解，不符合數學試題追求簡潔好懂、自然生長的高要求.考慮到該題在網絡上非常流行，故摘引時第（2）、（3）問中部分條件以“……”取代，節約版面.以下給出改編題.

改編題1如圖1，在等邊△ABC中，點D、P分別在邊CA、BC所在的直線上，直線BP、AQ交于點Q，且CD=BP.

（1）若點D、P分別在邊CA、BC上時，求證：AP=BD；

（2）若點D、P在射線CA和射線BC上時，請利用圖2求∠BQP的度數.

改編說明：將“陳題1”中第（2）問的變式統一在題干中，以條件“點D、P分別在邊CA、BC所在的直線上”呈現，這樣在第（1）問設置成特殊條件，強調“點D、P分別在邊CA、BC上”，而在第（2）問中放開到射線上進行研究.事實上，隨著探究的深入，如果作為習題講評課，還可啟發學生深入思考：如果點D、P在直線CA和直線BC上時，求∠BQP的度數.這樣設問，則需要學生全面討論，求解難度也將會上一個新的臺階.

陳題2如圖4，在平面直角坐標系中，已知A（0，a），B（-b，0），且a、b滿足

（1）求證：∠OAB=∠OBA.

（2）如圖4，若BE⊥AE，求∠AEO的度數.

（3）如圖5，若D是AO的中點，DE∥BO，點F在AB的延長線上，∠EOF=45°，連接EF，試探究OE和EF的數量及位置關系.

圖4

圖5

簡評：第（2）問就需要高超的構圖能力，且表述也不清楚，并沒有明確點E所在位置，圖形也只是示意圖；第（3）問陷入繁雜的圖形構造，對于限時考試來說，這樣的試題慎用為宜.基于以上商榷意見，筆者改編如下：

改編題2如圖6，在平面直角坐標系中，已知A（0，a），B（-b，0），P（p，0），且a、b滿足連接AB，作射線AP，過點B作BH⊥AP于點H.

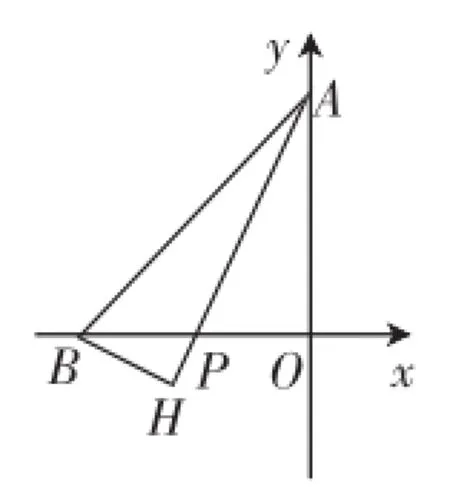
圖6

（1）當p=-1時.

①填空：線段AP為△AOB的_____；（直接填“角平分線”、“中線”或“高”）

②延長BH交y軸于點C，求證：BC＝AP.

（2）連接OH，求∠AHO的度數.

改編說明：首先是題干中明確了點P，善于讀題的學生應該清楚點P是x軸上一個動點，則圖6只是一個示意圖，點H會隨著點P的運動而變化；這為第（2）問的分類討論帶來啟示.有效考查了優秀學生嚴謹的思維品質；同時對學生讀句畫圖、構圖能力也有較好的考查.

陳題3如圖7，在四邊形ABDM中，AB＝BD，AB⊥BD，∠AMD＝60°，以AB為邊作等邊△ABC，∠ABD的平分線BE交CD于點E，連接ME.

（1）求∠BEC的度數；

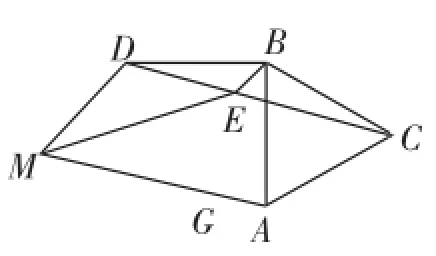
圖7

（2）連接EA，求證：EC＝ED+EB；

（3）求∠AME的度數.

簡評：主要難點在第（3）問，需要較強的構圖能力，這里提供兩種構造思考，如圖8、圖9都能實現第（3）問的思路貫通.

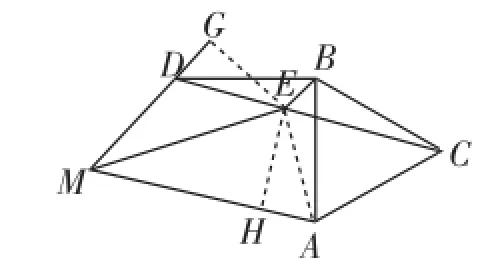
圖8

圖9

然而，就本題的第（2）、（3）問來看，關聯度并不緊密，且題干中的“∠AMD＝60°”在前兩問也沒有多大價值，所以改編時，筆者放棄了第（3）問，只是對前面兩問進行生長、拓展，改編為下面這道習題.

改編題3如圖10，在△ABD中，AB＝AD，∠DAB＝90°，以AB為邊作等邊△ABC，∠BAD的平分線AE交CD于點E.

（1）求∠AED的度數；

（2）求證：EC＝DE+AE；

圖10

（3）在射線AE上求作一點P，使∠ABP＝75°.（不寫作法，保留作圖痕跡）

改編說明：圍繞將“陳題3”中的∠BAD的平分線AE進行了開發，并且在洞察了圖形中很多特殊角度（如∠EDB=30°，連接EB，有∠EBD=30°）之后，在第（3）問提出尺規作圖，使之滿足“∠ABP＝75°”，隨著學生對圖10中各個角度認識的深度，將會有不同的作法，這里作法的繁簡與理解的深刻有直接的關系.比如，我們收集了三種典型的學生作法（圖11、圖12、圖13）.

圖11

圖12

圖13

可以發現，在圖11中，學生先作出一個60°角，再作60°角的平分線與AE相交于點P；圖12中，學生以BE為一邊，構造一個等邊△BEP，恰好交點在AE上；圖13中，學生只是“一道弧”就輕松搞定.事實上，筆者在相關數學研究QQ群是展示該題之后，有熱心的同行還用幾何畫板提供了不同的“一道弧”作法（圖14～17）.

圖14

圖15

圖16

圖17

二、關于陳題改編的三點思考

以上選取三個陳題及改編的題例，解讀、商榷并闡釋了陳題改編的心路歷程，以下再從整體上就陳題改編提出三點初步思考.

1.理解陳題，有的放矢推陳出新題

何明老師在文1中將一道“雙曲線”綜合題從300多字（外加兩個坐標系圖形）減少到100字（沒有圖形），命題打磨過程中由博返約、追求簡潔的示范意義讓筆者受益良多.然而要想追求試題的簡約呈現，需要我們在陳題改編之前，從不同角度貫通思路，提煉和洞察陳題的“深層結構”（羅增儒語）.在此基礎上還需要理解陳題系列設問的“并列”或“遞進”.一般來說，作為一道解答題下的系列設問建議設計成并列式問題，但體現遞進式求解的策略（詳見文2）.從這個角度來看，上文中的改編題2、改編題3都“有的放矢”地舍棄了陳題2、陳題3的第（3）問，正是想追求系列設問之間的遞進式求解策略.

2.精心構思，題干題肢預設關聯點

以上文中提及的陳題3來說，題干中的“∠AMD＝60°”在前兩問都沒有得到體現，像這樣的題干呈現就不符合簡潔呈現的追求，可以作為第（3）問的一個強化條件，使得題干更趨于簡潔好懂.這樣看來，在預設一道解答題時，就需要認真構思題干、題肢的條件呈現，而不宜把所有條件都“全面鋪開”，造成一些學困生閱讀和理解障礙.以筆者教學實踐來看，有些學困生在閱讀信息量、錯綜復雜的條件時常常容易讀漏或混淆條件，使得原本應該解答出來的第（1）、（2）問也不能順利解出.至于有些同行提出訓練學生從繁雜信息或條件呈現中“抗干擾”能力的考查要求，筆者則不敢認同，根本上說，這不符合“好的數學題目”應該“簡潔好懂、自然生長”（章建躍語）的價值追求.此外，就題肢之間的關系來看，不僅要追求上面提及的并列式問題與遞進式求解的思路暗示，還要思考題干信息與題肢之間的相容、包含或者邏輯連貫.比如，“改編題1”在題干中提到的是“點D、P分別在邊CA、BC所在的直線上”，而兩個題肢中分別是關于線段、射線的探究；再如，“改編題2”在題肢第（3）問中設計在射線AE上作出一點P，則讓題干中的角平分線保持著“生命活力”，而沒有讓題干中這個重要條件“提前死去”.

3.易進難出，把關設問引向更遠處

一般來說，解答題特別是作為全卷最后一題的把關題來說，應該努力追求易進難出，起點要低，吸引更多的學生參與.但是，作為最后一問又要使得問題具有必要的區分功能，就需要設計易錯點、障礙處加大難度，通過恰當的把關設問把學生的思考引向深入、走向遠處.比如，改編題1的第（3）問考查的是“點D、P在射線CA和射線BC上”，優秀學生在考后仍然可以思考“點D、P在射線AC和射線CB上”的情形；再如，改編題2的第（3）問“求∠AHO的度數”，如果學生只得到45°時，則說明思維還不夠嚴謹，缺少考慮點P在x軸正半軸的討論，教師在講評時可以從點P坐標特征的角度引導學生“回到概念”，理解坐標軸是直線、x軸上點的坐標特征等角度來突破，這樣重視“回到概念去解題”就能得到很好的落實.

1.何明.由博返約，追求簡潔——一道“雙曲線”綜合題的命題過程［J］.中學數學（下），2015（11）.

2.劉東升.“并列”式問題與“遞進”式求解——由一則解題教學案例說起［J］.中學數學教學參考（中），2012（8）.

3.劉東升.關聯性：一個值得重視的研究領域［J］.中學數學（下），2013（12）.H