一道“階段考題”的思路突破與講評設計

☉江蘇省張家港市梁豐初級中學蔣建東

一道“階段考題”的思路突破與講評設計

☉江蘇省張家港市梁豐初級中學蔣建東

考題的剖析和研究是教師常規教學工作的主要組成部分，也是教師教科研的一個方向，研究的價值在于：不僅可以服務于教學質量的提升、學習效果的優化，還可以促使教師專業水平的提升，服務于素質化教育改革的發展.因此，教師在教學過程中，開展深入而有效的考題研究是非常重要的，也是非常必要的.筆者就對近期初三階段性考試的一道壓軸題進行分析和研討.由此展開，欲以此達成拋磚引玉的效果.在最近一次初三階段性考試中，命題老師設計了一道把關題，是拋物線與圓的綜合考題，讓很多考生不適應，得分率極低，本文先展示該題的思路突破，并圍繞該題給出教學設計，最后對命題導向的話題給出相關思考，供研討.

一、“階段考題”的思路突破

（1）求b和c的值.

（2）若MN∥BC，

圖1

①連接CD、BN，判斷四邊形BCDN是否為平行四邊形，說明理由；

②以點D為圓心、DH長為半徑畫⊙D，點P、Q分別為拋物線和⊙D上的點，試求線段PQ長的最小值.

思路講解：（1）利用待定系數法容易求出b=-1，c=-4.

（2）①首先確認直線BC的解析式為y=x-4，于是直線MN的解析式為y=x.聯立拋物線的解析式y=x2-x-4和y=x-4，可解出點N的坐標，再計算出線段DN的長，與BC的長進行比較可以獲得解答.

②這個問題看上去較繁難，沒有思路，難以轉化到初中幾何中幾個圖形最值的模式（如兩點之間線段最短；垂線段最短；軸對稱最小值模式等），但是如果我們把問題稍作簡化，排除干擾圖形或線條的影響，就容易獲得思路了，如圖2，連接PD，交⊙D于Q，顯然DQ是定值（⊙D的半徑），故當PD最小時，PQ也就取得最小值！于是可以利用“兩點間距離公式”分析PD2的最小值，而D點是定點（1，1），即有PD2=（1-x）2+，真正的障礙出現了，就是對關于x的式子的整理變形，配方得到，故PD的最小值是，相應的PQ的最小值是.

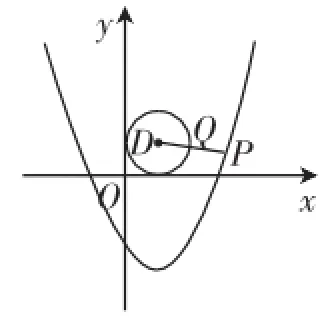
圖2

解后反思：最后一問的關鍵是坐標平面內一個定點到拋物線上任意一點之間的距離最小問題的研究，本質上是兩點間距離公式的使用，不然就需要構造直角三角形，利用勾股定理分析.也就是說，跟所謂的⊙D無甚關系，⊙D只是包裝、增加解題層次而已.理解上述關鍵或問題的深層結構之后，我們可以根據上述考題的講評與拓展設計出如下的教學流程，供研討.

二、“階段考題”的教學流程

圖3

問題1：能確定拋物線的解析式嗎？你有哪些不同的方法？

預設互動：學生可能會使用待定系數法直接代入解析式后得出關于b、c的二元一次方程組；也可以利用“兩根式”，設；還可以根據兩根坐標分析出對稱軸方程從而求出b.這樣可體現解法路徑的多樣化.這樣的教學不僅可以滿足班級每個層面的需求，還能激發部分優生深入、多元的思考，真正達成隱性分層、多元培優的效果.

問題2：求直線BC的解析式.

預設互動：學生可能會利用待定系數法求出直線BC的解析式，也可以根據直線斜率快速分析.由此可以進一步激發學生的參與，引領學生在自我參與的過程中達成溫故而知新.

問題3：將直線BC向上平移m個單位得到直線l，當直線l經過原點時，直接寫出直線l的解析式.

問題4：求直線l與拋物線對稱軸的交點坐標.

問題5：設直線l與拋物線在第一象限內的交點為M，求M點的坐標.

問題6：連接CD、BM，有人認為四邊形BCDM是平行四邊形，你覺得呢？

預設互動：問題3～6是原考題的（2）①，通過系列追問，化解求解的難點和主要步驟.這樣的問題鏈的產生不僅可以引領學生思考、啟發學生的思維，而且教師長期采用問題鏈的形式來進行啟發和引導，也培養了學生的思維習慣，提升了學生的思維能力，無形之中可以達成授之以漁的效果.

活動2：探究點到“線”的距離.

問題7：平面直角坐標系內，有點A（2，3），點A到y軸的距離是？點A到直線x＝1的距離呢？點A到直線y＝x的距離呢？

預設：通過變式問題，引導學生復習并思考點到直線的距離，作出垂線段是處理此類問題的關鍵.而關鍵環節的突破因為教師的提問和學生的體驗而悄然突破，達到潤物細無聲的效果.

問題8：平面直角坐標系中，有點D（1，1），該點到拋物線的頂點距離是多少？

問題10：平面直角坐標系中，點D（1，1），以點D為圓心、1為半徑作圓，若該圓上有一點Q，拋物線上有一動點P，試分析PQ的最小值.

預設互動：啟發學生回看“問題9”，與“問題10”相比有什么關聯？引導學生學會分析與類比，讓學生在對比中發現問題，找到突破口.

問題11：在問題10的條件下，過點P向⊙D引切線，設切點為G，當切線長PG取得最小值時，求點P的坐標.

預設互動：這個問題是“問題10”的再包裝，如圖4，要想PG取得最小值，只要在Rt△PDG中思考，DG是半徑為定長，斜邊PD取得最小值時，相應的直角邊PG也取得最小值，所以問題也就轉化到“問題10”.

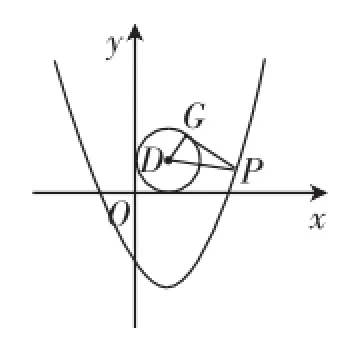
圖4

三、進一步的思考

1.思路突破重在引導學生排除干擾

我們在上面圍繞該題給出系列設問的主要目的是引導學生排除干擾，逐個擊破，一系列問題的價值在于設計鋪墊，縮小變式距離，幫助更多學生理解難題.從命題導向上來看，原考題中的多個小問之間并列式設計，背后缺少必要的關系或遞進式求解思路的啟示，也加大了最后一問的求解難度.此外，從命題應該追求簡潔、好懂、不超課標的目標來看，最后一問涉及繁難的數式變形、配方等，都超出了初中階段學生應該掌握的內容，不宜出現在高危害的考試中.

2.通過變式再練提高講評效果

根據教學經驗，一般較難問題如果在課堂上講評之后能聽懂的有一部分學生，當堂聽不懂的還會有一部分學生，這時如果直接追問學生是否理解，往往得到“聽懂”的回復，然而事實并非如此，對于較難題、易錯點，往往是貌似聽懂，實則不會求解的現狀，這時為了追求更好的解題教學效果，我們提倡跟進變式再練，通過變化字母、數字、圖形的位置等，不破壞原題的深層結構，這樣開展變式再練可以得到較好的效果.作為文末，我們圍繞考題給出變式再練.

如圖5，已知拋物線y＝-x2+bx+c交x軸于點A（-1，0）、B（3，0），交y軸于點C，連接BC，拋物線的對稱軸l分別交BC、x軸于點D、E.

（1）求b和c的值.

（2）求直線BC的函數解析式.

（3）若拋物線上有一點M（m，n），

圖5

①當m＝-2時，求點M到原點之間的距離；

②試分析點M到原點之間距離的最小值.

③試分析點M到點D之間距離的最小值；

（4）以E為圓心、1為半徑作圓，點P、Q分別為拋物線、⊙E上一動點，連接PQ，當PQ取得最小值時，求點P的坐標.

考題的研究到此其實并沒有結束，教師在課后還需

要做很多的工作，比如引導學生對類似的錯題進行整理和對比，對一類問題的研究進行總結和反思，在課堂的深入思維中，課后的變式訓練中，訓練后的反思中，不斷提升學生的解題能力，不斷提升學生的實際應用能力.

1.羅增儒.數學解題學引論［M］.西安：陜西師范大學出版社，2008.

2.【美】波利亞，著.怎樣解題［M］.閻育蘇，譯.北京：科學出版社，1982.

3.鄧東皋，孫小禮，張祖貴，編.數學與文化［M］.北京：北京大學出版社，1999.

4.鐘啟泉.“批判性思維”及其教學［J］.全球教育展望，2002（1）.Z