一道課堂例題的深思

☉江蘇省高郵市南海初級(jí)中學(xué)陳亞萍

一道課堂例題的深思

☉江蘇省高郵市南海初級(jí)中學(xué)陳亞萍

課堂上有效的例題教學(xué)，將反饋、鞏固和拓展學(xué)生對(duì)所學(xué)知識(shí)的理解與記憶，是學(xué)生掌握基本知識(shí)、基本技能，體會(huì)基本思想方法，積累基本活動(dòng)經(jīng)驗(yàn)的重要途徑.但是筆者聽(tīng)課中發(fā)現(xiàn)，大多數(shù)的課堂例題教學(xué)，常就題論題，較多地關(guān)注結(jié)果，而忽視例題中蘊(yùn)含的重要思想和方法及題目變式帶來(lái)的規(guī)律，這樣的例題教學(xué)就失去了其應(yīng)有的價(jià)值，也讓學(xué)生錯(cuò)失了學(xué)習(xí)過(guò)程中發(fā)展數(shù)學(xué)能力的機(jī)會(huì).

筆者近期聽(tīng)了一位年輕教師的課，此節(jié)課是“相似三角形性質(zhì)”的復(fù)習(xí)課，作為一名有經(jīng)驗(yàn)的教師，想必了解“相似三角形”是中考中的一個(gè)熱點(diǎn)，也是一個(gè)難點(diǎn)，在各省市的中考題中都有所涉及，但時(shí)常與函數(shù)、圓結(jié)合進(jìn)行考查.本文就從筆者聽(tīng)課過(guò)程中的一個(gè)片段入手，與讀者交流一些對(duì)例題教學(xué)的想法.

一、“片段”重現(xiàn)

授課教師在課堂上出示了這樣一道例題.

如圖，△ABC是一塊銳角三角形余料，邊BC=12，高AD=8，要把它加工成矩形零件，使矩形的一邊EF在BC上，其余兩個(gè)頂點(diǎn)分別在AB、AC上，設(shè)HE的長(zhǎng)為y，EF的長(zhǎng)為x.

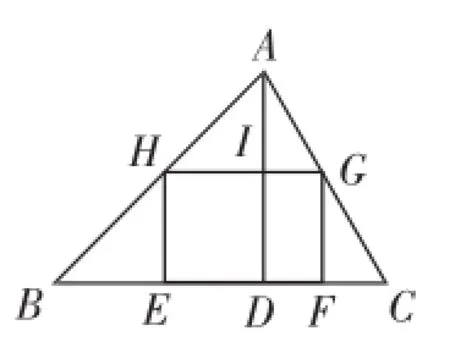
（1）寫出y與x的函數(shù)關(guān)系式；

（2）當(dāng)x取多少時(shí)，四邊形EFGH是正方形？

解：（1）由四邊形EFGH為矩形，得HG∥EF.

（2）當(dāng)y=x時(shí)，四邊形EFGH是正方形.

即x=4.8時(shí)，四邊形EFGH是正方形.

點(diǎn)評(píng)：本題是相似三角形的判定及性質(zhì)的綜合運(yùn)用，并用到了相似三角形對(duì)應(yīng)高之比等于相似比的結(jié)論，對(duì)于學(xué)生而言這類題的掌握是必要的，此題為典型例題，在考試中常會(huì)出現(xiàn).

課下，筆者找來(lái)幾個(gè)同學(xué)進(jìn)行詢問(wèn)：按照這樣的方法作矩形，什么情況下矩形的面積最大？所有學(xué)生都不加思索地回答：當(dāng)然是正方形的面積最大.學(xué)生的回答在筆者的意料之中，事實(shí)上，數(shù)學(xué)的終端評(píng)價(jià)試卷常關(guān)注最值問(wèn)題的考查，而這道題中矩形的面積是會(huì)發(fā)生改變的，授課教師為何不將這個(gè)最值讓學(xué)生試著求一下呢？雖然耽誤一些時(shí)間，但對(duì)學(xué)生思維的發(fā)展大有裨益.

于是筆者和這幾位同學(xué)進(jìn)行了交流，探討x為多少時(shí)，矩形EFGH的面積最大.

則當(dāng)x=6時(shí)，矩形面積會(huì)有最大值24.

思考：通過(guò)計(jì)算不難發(fā)現(xiàn)，正方形的面積不是最大的.這個(gè)結(jié)論的得出使學(xué)生豁然開(kāi)朗，也意識(shí)到“想當(dāng)然”不一定可取，上述解答實(shí)質(zhì)上運(yùn)用了二次函數(shù)，雖然學(xué)生未曾學(xué)過(guò)，但對(duì)于一個(gè)數(shù)的平方會(huì)產(chǎn)生最值卻很清楚，學(xué)生完全可以操作.從長(zhǎng)遠(yuǎn)的角度看，未學(xué)知識(shí)的滲透對(duì)于后繼的教學(xué)有很大幫助，當(dāng)學(xué)生初三學(xué)到二次函數(shù)的時(shí)候，會(huì)輕而易舉地掌握二次函數(shù)的相關(guān)知識(shí).倘若教師對(duì)未學(xué)知識(shí)的產(chǎn)生畏首畏尾，不敢適時(shí)滲透，對(duì)于學(xué)生的思維發(fā)展將會(huì)有很大阻礙.

二、提煉規(guī)律

筆者回班后，將該題改編.

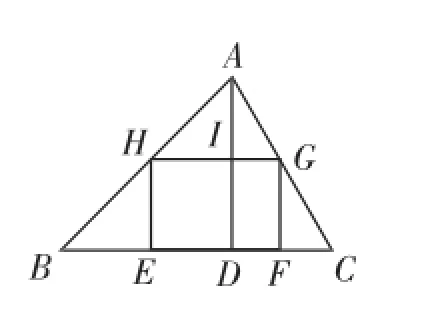
如圖，把△ABC加工成矩形，使矩形的一邊EF在BC上，其余兩個(gè)頂點(diǎn)分別在AB、AC上，當(dāng)HG滿足什么條件時(shí)，矩形EFGH的面積最大？

在筆者的引導(dǎo)下，學(xué)生深入思考后給出解答.

不妨設(shè)BC=a，高AD=b.

由四邊形EFGH為矩形，得HG∥EF，則△AHG∽△ABC，則

故當(dāng)HG是△ABC的中位線時(shí)，矩形EFGH的面積最大.

思考：學(xué)生在思考后回答了上述問(wèn)題，并給予了正確的解答，可見(jiàn)學(xué)生是有能力將該題解決的.教師要相信學(xué)生，更要給學(xué)生展示的機(jī)會(huì)，通過(guò)該生的解答，其余學(xué)生也清晰地認(rèn)識(shí)到當(dāng)HG為△ABC的中位線時(shí)矩形EFGH的面積最大，同時(shí)消除了原先正方形面積最大的設(shè)想，在潛意識(shí)里，學(xué)生也了解了二次函數(shù)是有最值的.

三、教學(xué)啟示

1.讓學(xué)生感受到好題的“價(jià)值”

何為“好題”？也就是蘊(yùn)含著豐富的思想和方法的題目，可以把眾多知識(shí)串起來(lái)的題目.事實(shí)證明，要使學(xué)生真正從題海中解放出來(lái)，要切實(shí)有效地大面積提高數(shù)學(xué)教學(xué)質(zhì)量，就要勇于沖破傳統(tǒng)教育思想和方法的束縛，徹底扭轉(zhuǎn)課堂教學(xué)中那種只重視結(jié)果、不重視過(guò)程的狀況，應(yīng)該在課堂上選擇好的例題，注意結(jié)果的發(fā)展及應(yīng)用過(guò)程的揭示和理解.在例題教學(xué)過(guò)程中，教師應(yīng)該努力為學(xué)生創(chuàng)設(shè)一個(gè)觀察、探索、研究問(wèn)題的機(jī)會(huì)，在理清思路、搞清原理的基礎(chǔ)上，將題目上升到一定的高度，揭示出新問(wèn)題的實(shí)質(zhì)和規(guī)律，只有這樣，才能使學(xué)生感受到好題的“價(jià)值”，讓思維得到真正的發(fā)展，水平得到真正的提高.

2.讓教學(xué)內(nèi)容“打破”常規(guī)局限

深層次的數(shù)學(xué)知識(shí)比表層知識(shí)更加重要，具有更高的學(xué)習(xí)價(jià)值，但有些深層的知識(shí)卻要運(yùn)用更多的理論，教師在例題教學(xué)時(shí)不應(yīng)該畏首畏尾，一成不變地遵循課本教學(xué)的順序，應(yīng)該適時(shí)地將未學(xué)知識(shí)滲透進(jìn)課堂，打破“常規(guī)”，這樣才能讓學(xué)生遨游課堂，理解更多、更有價(jià)值的數(shù)學(xué)問(wèn)題.

3.讓數(shù)學(xué)規(guī)律成為經(jīng)驗(yàn)之得

例題教學(xué)后及時(shí)的、卓有成效的回顧小結(jié)，既能使學(xué)生用較少的時(shí)間、較小的題量，達(dá)到同樣的效果，更重要的是有助于學(xué)生在原有的基礎(chǔ)上，進(jìn)一步建立起更為良好的更高層次的認(rèn)知結(jié)構(gòu)，實(shí)現(xiàn)“應(yīng)試教育”向“素質(zhì)教育”的轉(zhuǎn)變.例題教學(xué)后的變式很有必要，學(xué)生動(dòng)手實(shí)踐，真正讓數(shù)學(xué)的規(guī)律變成學(xué)生的經(jīng)驗(yàn)之得.

總之，數(shù)學(xué)例題教學(xué)要積極創(chuàng)設(shè)有價(jià)值的探究活動(dòng)，為學(xué)生提供一個(gè)探索發(fā)現(xiàn)的空間，并把知識(shí)融合起來(lái)，使每一個(gè)學(xué)生都真正動(dòng)起來(lái)，讓數(shù)學(xué)課堂煥發(fā)出生命的活力.Z