多元線性回歸模型在學生成績分析中的應用
王微

摘 要:考試對于學生來說可謂再尋常不過,小至隨堂測試,月考大至中考高考. 一名學生無論在哪個階段學習過程中,都會經歷許許多多次測試,每一次測試都會有成績記錄,如若將這些數據搜集起來數量是驚人的.
關鍵詞:多元線性;分析;學生成績
學生接受教育是連續的,所以評價一名學生不能只依靠某次考試成績,要縱向地連續觀察學生在各階段情況做綜合評價。中考成績是衡量學生進入高中之前學習情況的一項重要指標,所以選擇這兩個變量作為二模成績的解釋變量是含有一定的合理性。
圖3是學校類別x2,學生性別x3以及班級類別x4的直方圖,圖4表示的是二模成績y關于中考成績x1和一模成績x3的散點圖。通過觀察可以對新添加解釋變量的情況有初步了解。
R軟件對樣本數據做多元回歸得表4.可以得到多元線性回歸模型雖然已經得到回歸方程,但還要對模型的合理性進行檢驗。由上文多元回歸模型的理論可知,首先要對回歸方程做顯著性檢驗,分析數據發現該檢驗得到p值很小,與此同時相關系數R2為0.9298,說明建立的多元回歸模型比較合理,解釋變量能很好解釋因變量。
接下來還要對模型的解釋變量逐個進行t檢驗,表4中顯示中考成績、一模成績的p值很小,說明二者對二模成績影響很顯著。
學生性別這個變量對二模成績影響的p值為0.0271也很顯著。人們通知認為高中男生的學習能力要強于女生,但分析結果表明這種說法不是很正確。學生性別變量的回歸系數估計值為3.1393,表明女生成績普遍較好。高中階段的學習,不僅要求接受新知識能力強,而且要求有豐富的知識積累量。可能是女生學習態度較好,對知識掌握情況較好。
學校類別變量對因變量影響不是很顯著,也就是說學校水平對學生成績影響不大。樣本的五所學校可以分為兩個水平:重點高中和普通高中。學校水平不同對學生二模影響的功能貢獻率不是很大,這個結果與只有去好學校才有優異成績的想法不符。
二模成績與一模成績的散點圖說明一模成績可以很好的預測二模成績。圖中有很清晰的兩條直線,可能是由于學校所處水平不同引起的,重點高中學生成績整體上要比普通高中要好。圖5是多元回歸方程的殘差圖,圖中點散亂分布在y軸的兩側,說明所選擇的中考成績,學生性別等5個解釋變量可以很好的解釋二模成績,也就是說建立的模型有一定的合理性上述多元回歸模型殘差平方和,對上文五個解釋變量做顯著分析時知,學生個人對二模成績影響很大,學生類別與班額對學生成績影響不是很顯著。殘差平方和的意義在于除了學生個人之外其他所有因素對因變量的影響,其中也包括學校的教學質量。因此,我們就可以利用各自學校的殘差平方和去比較學校之間教學質量差異。利用上式可以得到每所學校的學校對學生的影響程度表示為
利用樣本數據計算得到的結果見表6.
從表6可以看出,C、D兩所學校殘差平方和比較大,表明與其他幾所學校有明顯差異。從實際意義上看,說明這兩所學校在師資力量、辦學條件、生源質量等方面與其他三所學校有很大不同。
模型拓展
本文之前的分析都是在樣本數據的基礎上,利用數據中包含比較直觀的信息(學生成績、性別等),從學生角度分析影響學生的二模成績因素。在樣本中沒有任何關于學校辦學條件,師資力量等代表學校教學質量相關信息情況下,是否可以利用簡單線性回歸模型挖掘出潛藏在樣本中的信息,進而估測學校的教學質量的差異為學校排名。
其中表示來自第i所學校的第j學生的第二次模擬考試成績。
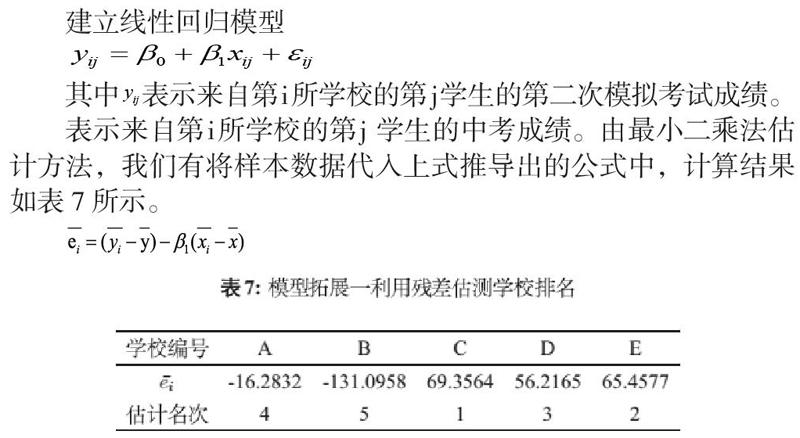
表示來自第i所學校的第j 學生的中考成績。由最小二乘法估計方法,我們有將樣本數據代入上式推導出的公式中,計算結果如表7所示。
數據分析之前,已經大致了解學校的基本情況。其中學校編號為CDE的三所學校為省級示范高中,編號為AB的兩所學校為普通高中,實際學校排名情況與上表現是排名大體一致。
本文建立的多元回歸模型對三組學生成績分別從學生以及學校角度進行分析,并結合統計學知識、R軟件對數據分析處理的結果進行了有效的分析與合理解釋。
當統計學與數據相遇總會有這樣那樣的火花,不一樣的風景。樣本只包含幾次考試成績和關于學生自身的一些信息,沒有直接關聯教學質量的信息。但是簡單的分析就可以挖掘到許多隱藏在數據背后的信息,這就是統計學的魅力所在。通過上述分析再一次驗證了數據力量是巨大的,合理、高效地利用為教學服務,將具有重大的意義。
參考文獻:
[1] 朱姝帆. 湖北省農村居民家庭人均收入影響因素分析——多元線性回歸分析[J]. 科技創業月刊. 2009(01).

