基于IOWA的中國海洋生物醫藥業組合預測模型的應用研究

鄭　莉，張玉潔，李琳琳

（國家海洋信息中心，天津 300171）

【統計與分析】

基于IOWA的中國海洋生物醫藥業組合預測模型的應用研究

鄭莉，張玉潔，李琳琳

（國家海洋信息中心，天津 300171）

基于誘導有序加權平均算子的組合預測方法是近年來發展起來的具有廣泛應用的預測模型。首先采用指數平滑模型、ARIMA模型及多元回歸模型建立了中國海洋生物醫藥業增加值的單項預測模型；隨后引進誘導有序加權平均 （IOWA）算子的概念，建立了海洋生物醫藥業增加值的組合預測模型，實證結果表明組合模型能有效提高預測精度；最后利用組合模型對 “十三五”期間中國海洋生物醫藥業發展趨勢進行了預測分析。

海洋生物醫藥業；誘導有序加權平均算子；組合預測；海洋經濟；海洋產業

引言

中國海洋自然條件優越，海域遼闊，大陸海岸線長達18 000多千米，海洋資源種類繁多，海洋生物資源儲備豐富。中國現代海洋藥物的研究始于20世紀70年代，隨后海洋生物藥物產業也快速發展起來，產生了可觀的經濟效益。當前中國海洋生物產業處于起步向全面產業化發展的關鍵時期，隨著國家對海洋生物醫藥業政策扶持和投入力度的逐步加大，海洋戰略性新興產業中的海洋生物醫藥業發展正行駛在快車道。適時加快對海洋生物醫藥業發展的宏觀分析與預測研究對于確定全國海洋生物醫藥業增長目標和海洋開發戰略將具有重要的實踐和參考意義。本文將以海洋戰略性新興產業——海洋生物醫藥業為例，對海洋生物醫藥業增加值建立動態組合預測模型，為其它海洋產業發展趨勢預測提供一定的借鑒。

1　誘導有序加權組合預測模型簡介應用情況

國內外許多學者和機構都對海洋生物醫藥業的預測方法進行了廣泛研究，主要方法為時間序列分析法、灰色預測法、情景分析法等，但組合預測的文獻較少。組合預測可以綜合利用各種預測方法所提供的信息，提高預測的精確度和可靠性。Bates和Granger（1969）［1］首次提出了組合預測的概念，即通過確定各單項預測方法的加權平均系數，以適當權重將不同的單項預測方法進行組合。基于組合預測的思想，Yager（1999，2002）［2，3］提出誘導有序加權平均（IOWA）算子，通過引入IOWA算子，根據各單項預測方法在樣本區間上各時點的擬合精度的高低按順序賦權，以誤差平方和為準則建立一種動態組合預測模型。國內學者陳華友（2003，2005）［4，5］最先使用誘導有序加權的預測方法，并證明該方法相比于傳統的廣義加權算術平均組合預測方法具有更高的精度，各種預測誤差指標值均低于傳統方法。這種方法克服了傳統靜態組合預測模型在集成時存在對單項預測方法以固定權系數賦權的缺陷，可以對不同時期的單模型預測結果進行動態集成。

誘導有序加權平均組合預測模型基本計算過程如下［4-6］。

1.1計算預測精度

設某經濟現象的指標序列有觀察值為 ｛yt，t=1，2…，N｝，有m種可行的單項預測方法，設yt為第t時刻的真實值，為第t時刻第種方法的預測值。i=1，2，…，m；t=1，2，…，N。w1，w2，…，w3為單項預測方法在組合預測中的加權系數，滿足

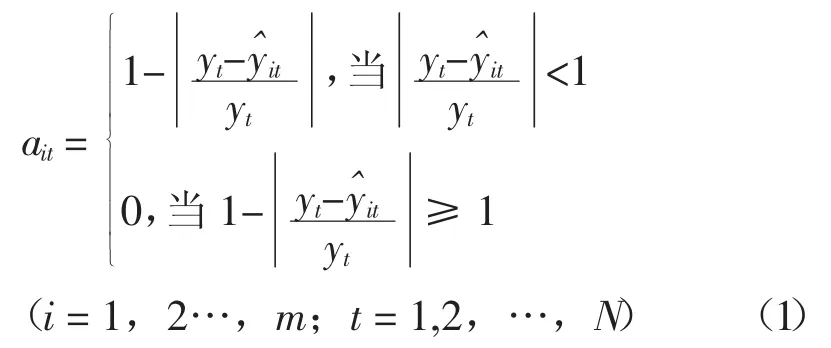
稱ait表示第i種預測方法第t時刻預測精度，或預測值的誘導值，若：顯然，ait∈［0，1］預測度反映了預測模型的擬合值與實際值擬合程度的優劣。

1.2確定IOWA算子組合預測值

將ait看成的誘導值，構建m個二維數組并按從大到小的順序排列預測精度序列a1t，a2t，…，amt，對排序后的預測值分別賦以權重。則可確定IOWA算子的組合預測值：

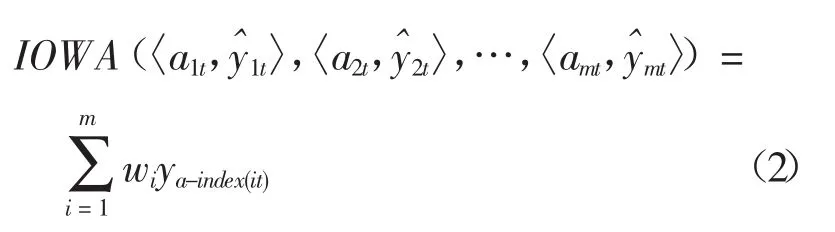
式中：a-index（it）是第i個大的預測精度的下標，W=（W1，W2，…，Wm）T為各單項預測方法在組合預測中的IOWA算子的加權向量。顯然，新的組合預測的賦權系數與單項預測方法在各時點上的預測精度大小密切相關，預測精度高就優先賦大一點的權系數。

1.3建立基于IOWA算子的組合預測模型

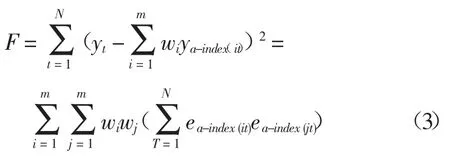
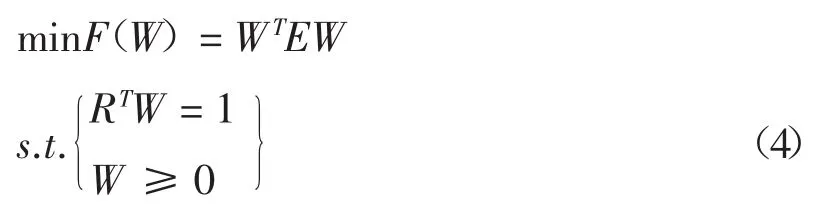
式中：R=（1，1，…，1）T，W=（W1，W2，…，Wm）T，上述規劃實際上是一個二次規劃，可利用Kuhn-Tucker條件將其轉化為線性規劃或直接用matlab最優化工具箱來求解出最優權系數

1.4基于IOWA算子的組合預測模型的預測

通過上文二次規劃模型求解可以獲得樣本區間上組合預測IOWA最優權系數，設W*=根據預測連貫性的原則，可進行預測區間［N+1，N+2，…］的基于IOWA算子組合預測，公式為：

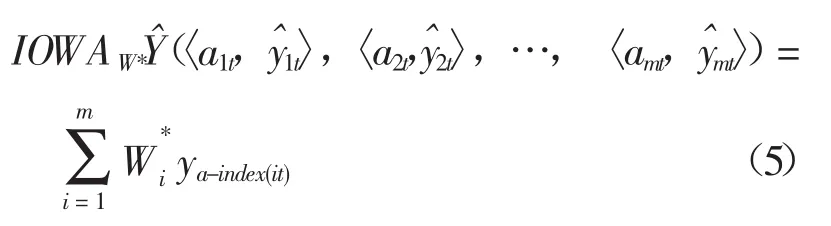
式中：t=N+1，N+2，…，在預測區間 ［N+ 1，N+2，…］上，a1t，a2t，…，amt（預測精度序列）的大小是根據各單項預測方法在樣本區間上近幾期擬合平均精度的高低來確定。即要進行未來k步的預測時，用第i種預測方法最近的k期擬合平均精度來反映預測區間上第期的預測精度。

在應用方面，胡彥（2009）［7］等建立基于IOWA算子的稅收組合預測模型，夏立福等（2011）［8］以實際工程為例，將IOWA算子組合預測結果與單一模型結果進行比較，驗證了IOWA算子組合預測方法的實用性。吳鳳平（2013）［9］采用BP神經網絡和GM（1，1）作為單項預測模型，對連云港港口吞吐量建立了基于IOWA算子的組合預測模型，并驗證了該模型預測精度優于各單一預測模型，各項誤差指標都低于其他兩種預測方法。盡管IOWA算子組合預測方法具有比傳統預測方法更精確，更穩定的預測結果，但基本尚未應用在海洋經濟預測領域，本文擬在海洋經濟領域引入IOWA算子的組合預測模型，選取海洋生物醫藥產業為例，對海洋生物醫藥業增加值建立動態組合預測模型。

2　中國海洋生物醫藥業增加值預測實證研究

下文將對中國海洋生物醫藥業增加值建立指數平滑模型、ARIMA模型及多元回歸模型3種模型，并在此基礎上進行組合預測研究［10-12］。其中，建模數據來源于《中國海洋統計年鑒》（2002—2014年）及《2014年中國海洋經濟統計公報》。圖1描述了中國海洋生物醫藥業增加值走勢（2001—2014年）。

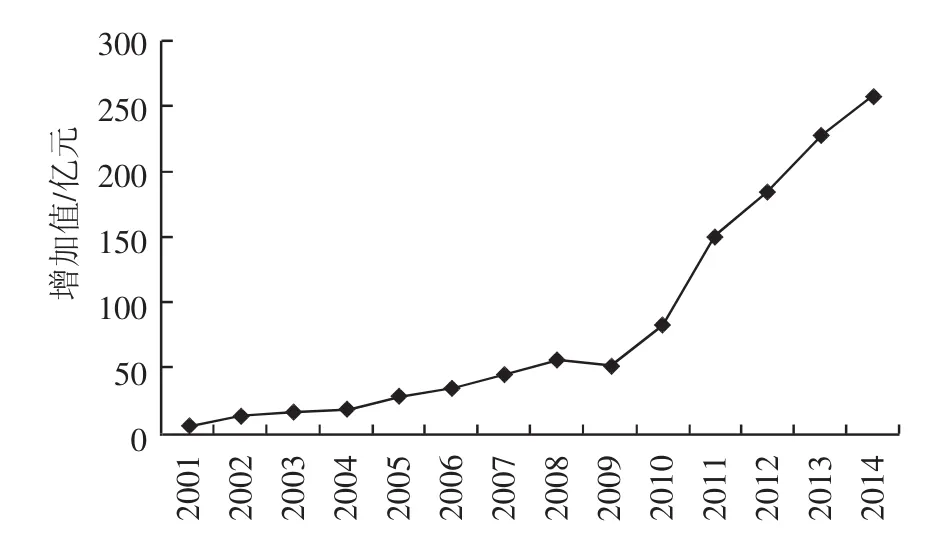
圖1　2001—2014年中國海洋生物醫藥業增加值Fig.1　The added value of China's marine biomedicine industry from 2001-2014

2.1單項預測模型

2.1.1指數平滑模型

指數平滑法適用于不具有明顯的季節波動和趨勢變動的單指標時間序列數據。指數平滑法分為單指數平滑法、雙指數平滑法、Holt-Winters乘法模型、Holt-Winters加法模型和Holt-Winters無季節性模型，其中Holt-Winters無季節性模型適用于具有時間趨勢但無季節變化的序列，對于中國海洋生物醫藥業增加值數據序列yt，可以采用這種方法進行預測，yt平滑后的序列y^t的計算式為：y^t+k=at+btk，k＞0，其中at表示截距，bt表示斜率，這兩個參數定義為下列遞歸式：

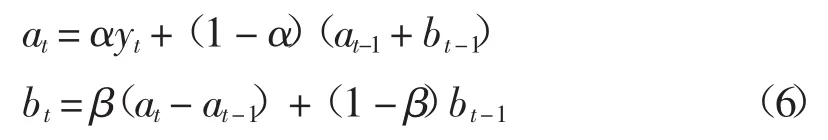
式中：α、β取值在［0，1］之間，稱之為阻尼因子。預測值就可以由下式計算：

利用2001—2014年海洋生物醫藥業增加值數據，利用Eviews軟件建立Holt-Winters無季節性模型，得到α、β值分別為1、0.57。通過上述指數平滑模型得到2003—2014年中國海洋生物醫藥業增加值見表1。

2.1.2ARIMA模型

ARIMA模型是被廣泛運用于對各類時間序列數據分析和建模的方法。模型基于如下的觀念：要預測的時間序列是由某個隨機過程生成的。如果生成序列的隨機過程不隨時間變化，則該隨機過程的結構可以被確切地刻畫和描述。利用序列過去的觀察值，可以外推出序列的未來值。在ARIMA模型中，序列的未來值被表示成滯后項和隨機干擾項的當期及滯后期的線性函數，即模型的一般形式如下式所示：

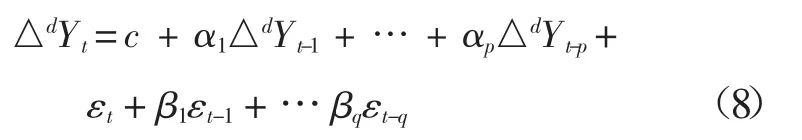
上述模型稱為ARIMA（p，d，q）模型，其中，Yt是d階單整序列，由一個自回歸模型AR（p）和一個移動平均模型MA（q）組成，p為模型的自回歸項數，q為模型的移動平均項數。其中，Yt是自回歸移動平均序列，c為常數，α1，…，αp表示自回歸系數，β1，…，βq表示移動平均系數，εt是相互獨立的白噪聲序列。

根據上述建模過程，利用2001—2014年數據，對中國海洋生物醫藥業增加值序列建立ARIMA（0，2，2）模型，方程估計結果如下：

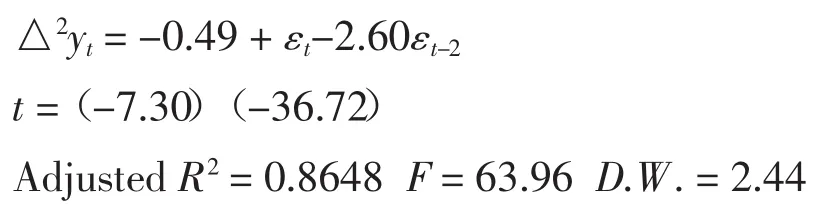
采用上述建立的ARIMA模型并通過靜態預測法，可得到2003—2014年中國海洋生物醫藥業增加值見表1。

2.1.3多元回歸模型

多元回歸模型的基本表達式如下：

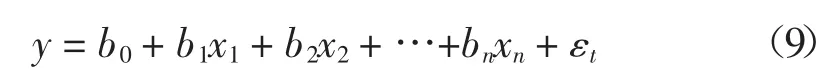
式中：y為因變量，x為自變量，b0，b1，…，bn為待估計參數。最常見的參數估計方法為最小二乘估計法。多元回歸模型包括線性回歸及非線性回歸，有多種變形，其中自變量可取對數、指數、冪指數等多種形式。

本文將對中國海洋生物醫藥業增加值建立基于生產函數的回歸方程并預測。回歸方程的解釋變量包括資本投入、勞動力投入。由于海洋生物醫藥業時間序列較短，本文假定規模報酬不變即α+β=1，通過對C-D生產函數的一般形式進行變形（其中，Y、K、 L分別表示產出量、資本、勞動投入量，α、β分別表示資本、勞動的產出彈性，A0為常數，表示基年的技術水平，r也是常數，表示科技進步增長速度，t表示時間，A0ert表示t年的綜合科技水平），得到新的形式這一模型形式可以節省自由度。從圖1可以看出，2009年中國海洋生物醫藥業增加值減少，究其原因，主要是受2008年的金融危機的影響。為了能夠捕捉到突發事件對回歸模型的影響、提高預測精度，本文在回歸模型中設置了虛擬變量dum09，將該變量2009年數值設置為1，其它年份設置為0。其中海洋生物醫藥業的資本變量沒有統計數據，用沿海地區固定資本投入乘以海洋生物醫藥業增加值占全國海洋生產總值比重進行替代，建立如下回歸模型：

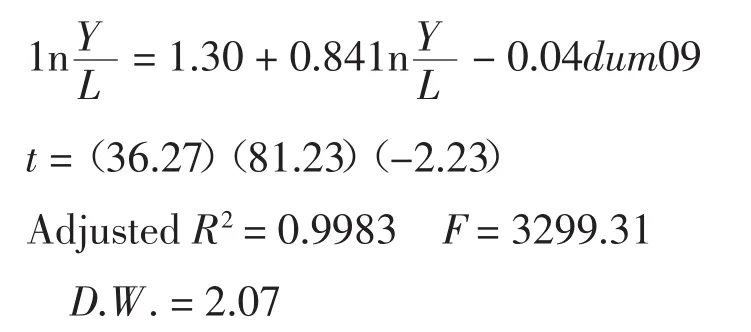
采用多元回歸模型得到的2003—2014年中國海洋生物醫藥業增加值見表1。

2.2基于IOWA算子的組合預測模型

用上述三種單項模型分別對中國2003—2014年的海洋生物醫藥業增加值進行預測，隨后根據三種單項模型的預測結果建立基于IOWA算子的組合預測模型，并計算組合權重。根據式（1）可以得到三種模型在各個時點處的預測精度序列，從而可以構造出第t時刻預測精度和其對應在樣本區間的預測值的二維數組如表1。

按式（2）對上表計算IOWA組合預測值，下面t=1，2以簡要說明計算過程，當t=1時：

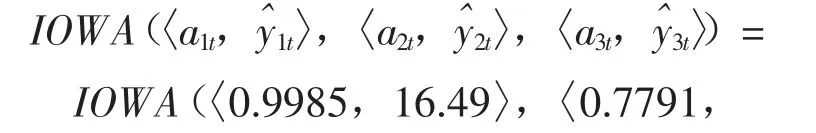
同理可得t=3，…，11的IOWA組合預測值，根據式（3）和式（4），得如下最優化組合模型：

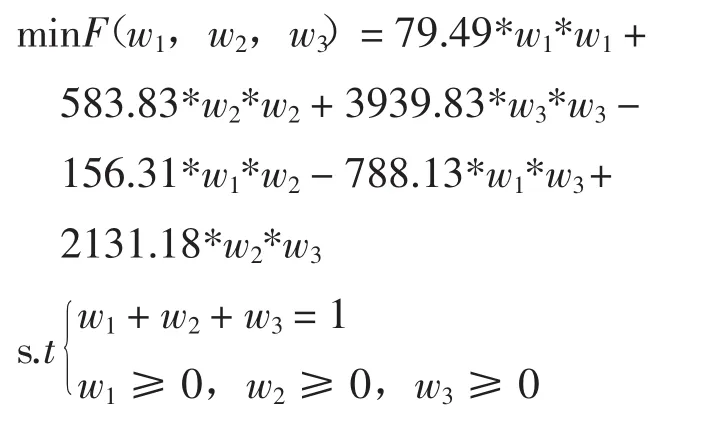
對上式利用Matlab最優化工具箱計算得到基于IOWA的組合預測模型的最優權系數為：則在t時刻組合預測模型的預測值為：

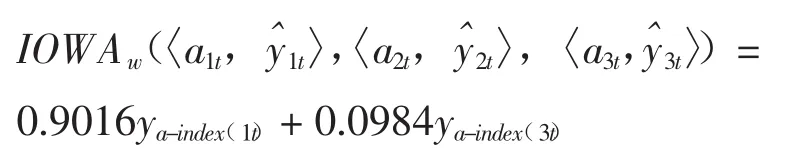
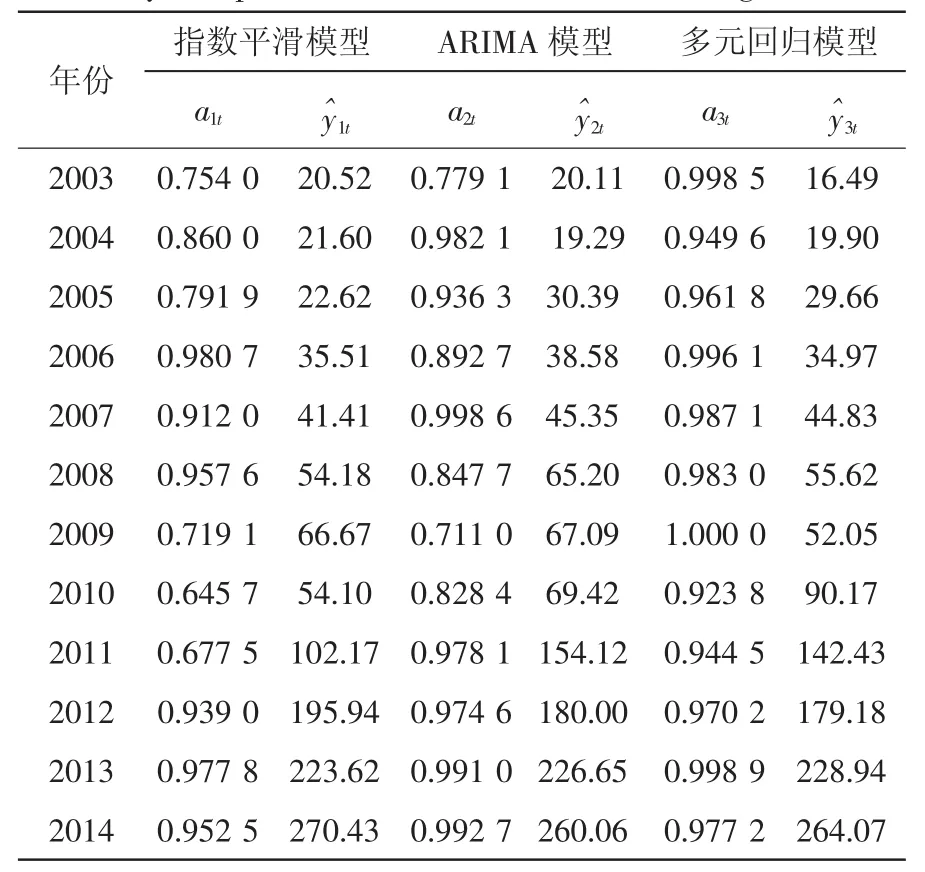
表1　三種單項預測方法預測精度及預測值二維數組Tab.1　Two-dimensional arrays consisting of prediction accuracy and predictive value of three forecasting methods

由上述組合模型知，時刻預測精度排名第二的單項預測法對應的權系數取值零，說明該時刻對應的單項預測方法冗余，這和傳統的組合預測方法的權系數的計算有很大的不同。

2.3模型的評價及預測

一般模型比較方法有絕對數值比較和相對數值比較，其中均方根誤差和平均絕對誤差屬于絕對數值比較，而平均絕對百分比誤差和希爾不等系數屬于相對數值比較［4-13］。由于均方根誤差的應用原理與平均絕對誤差基本一致，選一種即可，因此最終選擇平均絕對百分誤差、均方誤差和希爾不等系數進行模型的評價。一般認為平均絕對百分比誤差（MAPE）的值低于5%，則預測精度很高；均方根誤差越小越好；希爾不等系數（Theil IC）的值介于0～1之間，且值越小，模型的精度越高。其中，

平均絕對百分比誤差：

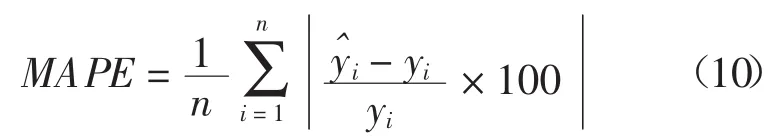
均方根誤差：

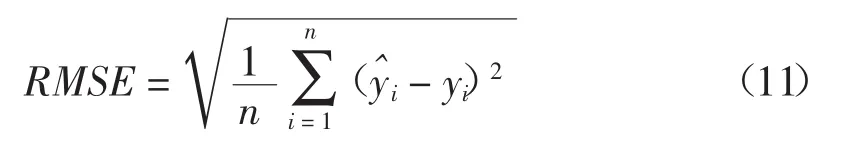
希爾不等系數：

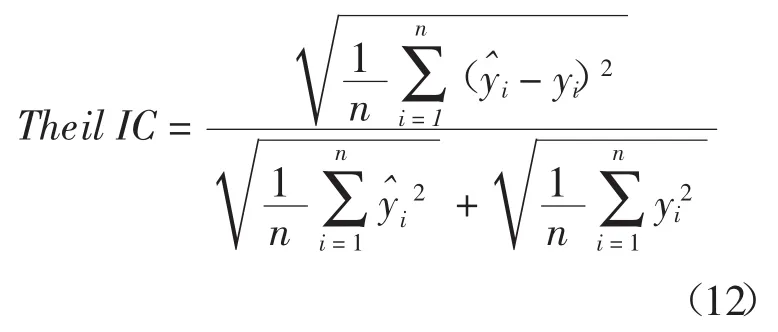
選取2003——2014年中國海洋生物醫藥業增加值單項模型預測及組合模型預測數據計算預測誤差，從而進行模型評價，結果見表2及表3。由表2中結果可知，多元回歸模型的MAPE值、RMSE值和Theil IC值較其它單項模型都小，且組合預測模型的MAPE值、RMSE值和Theil IC值均小于所有單個預測模型，同時也小于簡單算術加權組合預測模型。由此可見，組合預測模型比單項預測模型的精度要高，同時比傳統簡單算術加權平均組合預測精度高，從而表明基于IOWA算子的海洋生物醫藥業增加值組合預測模型具有效性和優越性，是優性組合模型。從表3中結果可知，基于IOWA算子的組合模型具有很強的預測性，所有年份的預測誤差均在5%以內。此外，由圖2可看出，所有預測方法中，基于IOWA算子的組合模型預測值曲線與實際值曲線最為接近。

從前面的分析可得知，如果所選取的模型的信息具有很強的互補性，那么模型的預測誤差將會更大幅度的降低，因此單項預測模型的選取在組合預測模型中是非常重要的。

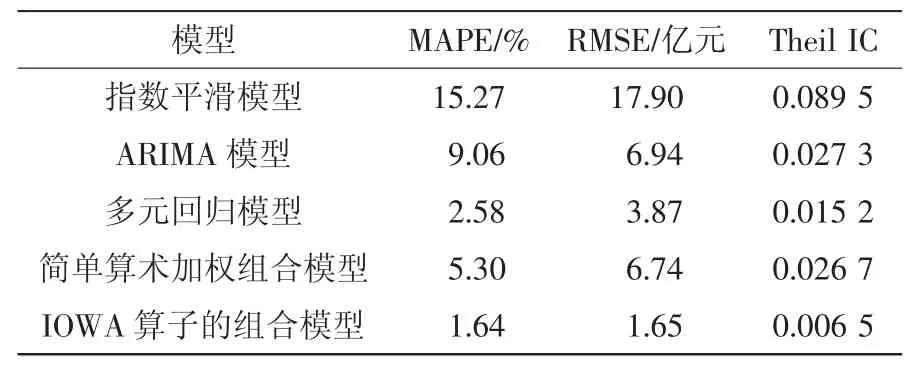
表2　各個預測模型評價結果Tab.2　Evaluation results of each model

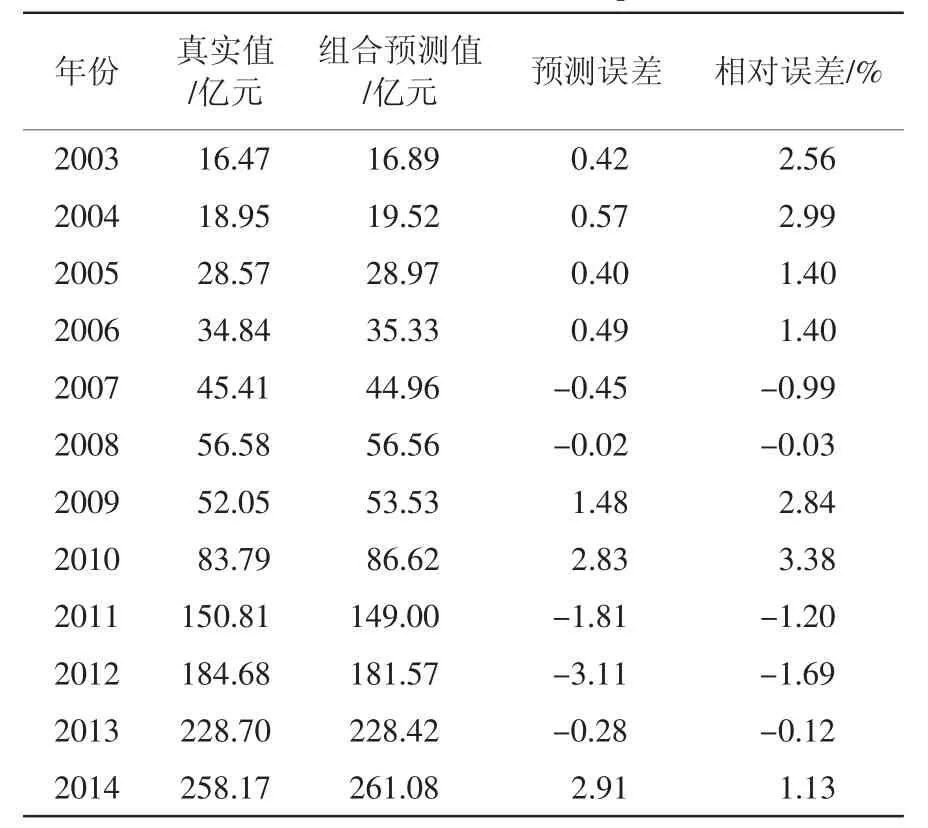
表3　基于IOWA算子的組合預測模型結果及評價Tab.3　Result and evaluation of the combined forecasting model based on the IOWA operator

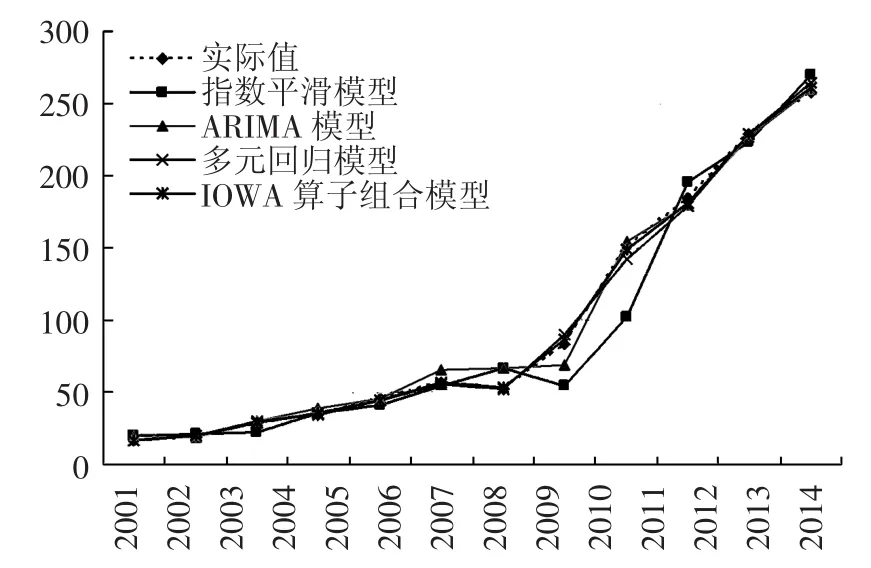
圖2　2003—2014年中國海洋生物醫藥業增加值實際曲線和擬合曲線Fig.2　The actual curve and fitting curve of the added value of China's marine biomedicine industry from 2003-2014

3　“十三五”時期海洋生物醫藥業預測及分析

根據上述單項模型及組合預測模型對2015至2020年中國海洋生物醫藥業增加值進行實證預測，其中，為了預測2015—2020年海洋生物醫藥業增加值，需要對回歸模型中自變量進行預測，對于海洋生物醫藥資本變量預測采用ARIMA（1，1，1）模型預測，海洋生物醫藥業涉海就業人員采用指數平滑法預測。結果如表4所示。

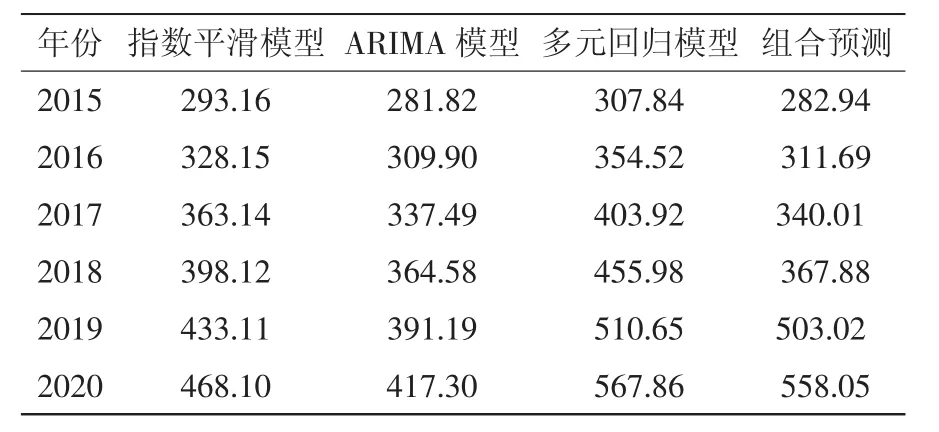
表4　“十三五”時期中國海洋生物醫藥業增加值的預測值Tab.4　Forecast results of the added value of China's marine biomedicine industry during the 13th Five-Year Plan period　億元

由表4知，預計到2020年，中國海洋生物醫藥業增加值將達到558億元，“十三五”期間海洋生物醫藥業增加值的增速將達到14.6%（現價）。在國民經濟新常態大背景下，隨著中國海洋強國及海上絲綢之路戰略的實施，經濟體制改革和創新驅動的推進，以及國家和地方政府政策的大力支持，“十三五”期間中國海洋經濟將逐步進入轉型期，經濟增長轉入中高速、結構優化、效益提高、民生改善。海洋生物醫藥固定資產投資屬于產業發展前期投入，由上文建立的多元回歸模型可知，海洋資本的產出彈性為0.84，勞動力產出彈性為0.16，可見海洋生物醫藥業是資本密集型產業，符合海洋新興產業發展特征，明顯區別于傳統海洋產業過分依賴于勞動力投入的發展模式。因此可以預期，作為海洋戰略性新興產業，海洋生物醫藥業將順應國內外經濟形勢變化，增速將放緩。

4　結語

本文首次將IOWA算子組合預測方法引入到海洋經濟預測領域，動態集成了指數平滑模型、ARIMA模型、回歸模型三種方法對中國海洋生物醫藥業增加值數據進行了擬合，并對“十三五”期間中國海洋生物醫藥業的發展趨勢進行了預測。在單模型預測時，本文的創新點在于在多元回歸模型預測中，加入了突發事件虛擬變量，并對自變量采用了ARIMA模型進行預測。結果顯示利用IOWA算子組合預測方法對其進行動態集成，集成后的誤差得到了有效地控制，且全部控制在5%以內，預測精度較單項方法的預測精度得到大大提高。

但是，本文依然存在著一定的不足之處，可以在下一步的研究中進行創新和改進。首先，進行單模型預測時，由于本文預測對象可搜集到的數據較少，一些時間序列模型的預測效果并不是特別顯著，可以嘗試利用處理小樣本的一些模型進行建模預測，達到提高預測精度的目的。其次，在組合預測時，本文采用了動態組合預測方法，大大降低了預測誤差。但是，這種組合預測方法自身也存在一定的缺陷，比如說，在某些年份如果單模型預測結果都偏大，則最后組合預測的結果一定偏大，在今后的研究中將組合預測模型與專家意見集成對上述缺點進行改進將會是未來研究的一個方向。

［1］Bates J M，Granger C W J.The combination of forecasts［J］.Operational Research Quarterly，1969，20（4）：451-468.

［2］Yager R R.Induced ordered weighted averaging operators［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B，1999，29（2）：141-150.

［3］ Yager R R.Using fuzzy methods to model nearest neighbor rules［J］.IEEE Transactions on Systems，Man and Cybernetics，Part B，2002，32（4）：512-525.

［4］陳華友，劉春林.基于IOWA算子的組合預測方法 ［J］.預測，2003，22（6）：61-65.

［5］ 陳華友.組合預測方法有效性理論及其應用 ［M］.北京：科學出版社，2008.

［6］郭金童，趙光明.基于IOWA的中國能源需求組合預測模型的應用研究［J］.未來與發展，2010，1：68-72.

［7］胡彥，李秀美，陳華友．基于IOWA算子的稅收組合預測模型［J］．統計與決策，2009（10）：33-35．

［8］夏立福，李井春，王洪海.基于IOWA算子的組合預測模型研究及應用 ［J］．測繪與空間地理信息，2011，34（1）：208-212.

［9］吳鳳平，曹艷國.基于IOWA算子的港口吞吐量組合預測方法［J］.水利經濟，2013，05：11-14+75.

［10］姜繼嬌，楊乃定．基于IOWA算子的行為證券組合投資決策研究［J］．系統工程理論與實踐，2004（11）：57-62．

［11］王應用，羅英.廣義加權算術平均組合預測技術研究［J］.預測，1998，17（1）：51～53.

［12］盧二坡.組合模型在中國能源需求預測中的應用 ［J］.數理統計與管理，2006，25（5）：505-511.

［13］丁晨芳．組合模型分析方法在中國糧食產量預測中的應用［J］．農業現代化研究，2007（1）：101-103．

Applied Research on Combined Forecasting Model of China′s Marine Biomedicine Industries Based on Induced Ordered Weighted Averaging Operators

Zheng Li，Zhang Yujie，Li Linlin
（National Marine Data and Information Service，Tianjin 300171，China）

The method of combination forecasting based on the induced ordered weighted averaging operator has been developed in recent years and used in a wide range of applications.Firstly，we respectively make use of exponential smoothing model，ARIMA model and multiple regression to construct models of added value of China′s marine biomedicine industry.Secondly，by introducing the concept of induced ordered weighted averaging operator，we construct the combination forecasting model of added value of marine biomedicine industry.The empirical results show that the combined forecasting model can effectively improve the prediction accuracy.Finally，we predict the development trend of China′s marine biomedicine industry during the 13th Five-Year Plan period by using the above combination forecasting model.

marine biomedicine industry；IOWA operator；combination forecasting

F224

A

2095-1647（2016）01-0038-08

2016-02-05

鄭莉，女，助理研究員，主要研究方向為海洋經濟統計、預測分析，E-mail：zhengli_668@126.com。