以生為本　智慧引思——以蘇教版二年級下冊“有余數(shù)的除法”教學(xué)為例

江蘇東臺(tái)市實(shí)驗(yàn)小學(xué)（224200）　陳松蘭

以生為本智慧引思——以蘇教版二年級下冊“有余數(shù)的除法”教學(xué)為例

江蘇東臺(tái)市實(shí)驗(yàn)小學(xué)（224200）陳松蘭

作為課堂教學(xué)的引導(dǎo)者，教師要智慧地處理“讓學(xué)”與“引思”的關(guān)系，教師要適時(shí)“引”、有效“引”、智慧“引”，課堂才會(huì)真正實(shí)現(xiàn)以生為本。

引思知識(shí)生長點(diǎn)思維斷層處智慧碰撞處

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011）版》指出，學(xué)生的學(xué)習(xí)應(yīng)當(dāng)有足夠的時(shí)間和空間經(jīng)歷觀察、實(shí)驗(yàn)、猜想、計(jì)算、推理、驗(yàn)證等活動(dòng)。高效的數(shù)學(xué)課堂中，教師應(yīng)做學(xué)生學(xué)習(xí)的引導(dǎo)者，做學(xué)生學(xué)習(xí)的引路人，智慧引思，促學(xué)生發(fā)展。

一、引思，“引”在知識(shí)生長點(diǎn)

“好的學(xué)習(xí)，不是來自教師找到了一種好的教學(xué)方法，而是來自給學(xué)生更好的機(jī)會(huì)去建構(gòu)。”教師要立足學(xué)生學(xué)情，以學(xué)生已有的知識(shí)和觀念作為新知識(shí)教學(xué)的起點(diǎn)，順著學(xué)生的知識(shí)生長點(diǎn)，“引”學(xué)生獨(dú)立思考。

【課例1】“分?jǐn)?shù)的意義”教學(xué)片斷

師：這塊餅?zāi)軗Q成一個(gè)西瓜嗎？能換成一個(gè)蘋果嗎？……所以這塊餅代表的是什么？（一個(gè)物體）

師生共同小結(jié)，得出單位“1”：

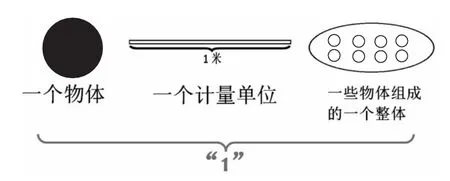
這里，教師精心設(shè)計(jì)研究素材，激發(fā)學(xué)生已有的知識(shí)經(jīng)驗(yàn)，為學(xué)生對新知識(shí)的深入研究奠定基礎(chǔ)；立足學(xué)生學(xué)習(xí)的最近發(fā)展區(qū)，通過連續(xù)追問的三個(gè)問題，在知識(shí)生長點(diǎn)處適時(shí)“引”，使學(xué)生的思維走向?qū)嵸|(zhì)，學(xué)生對單位“1”的理解也逐步走向深入，對概念的認(rèn)識(shí)也進(jìn)一步清晰、深化。

二、引思，“引”在思維斷層處

心理特點(diǎn)決定了學(xué)生的思維具有一定局限性，學(xué)生對知識(shí)的理解往往呈現(xiàn)片面性、定式性、呆板性。教師應(yīng)全面分析了解學(xué)生和教材，在學(xué)生思維斷層處“引”思，拓展學(xué)生的認(rèn)知，彌補(bǔ)學(xué)生的不足。

【課例2】“商不變的規(guī)律”教學(xué)片斷

1.課件出示：計(jì)算下面各題，你有什么發(fā)現(xiàn)？

（54×2）÷（18×2）=

（54×3）÷（18×3）=

（54×5）÷（18×5）=

（54÷6）÷（18÷6）=

（54÷9）÷（18÷9）=

（54÷18）÷（18÷18）=

我的發(fā)現(xiàn)＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

2.小組交流自己的計(jì)算及發(fā)現(xiàn)。

3.全班交流匯報(bào)。

（學(xué)生自由匯報(bào)結(jié)果，教師適時(shí)引導(dǎo)）

師：大家發(fā)現(xiàn)的這個(gè)規(guī)律是不是只適用于“54÷18”呢？我們要確定這個(gè)規(guī)律，還需要干什么？

生：需要進(jìn)一步驗(yàn)證其他算式是否也存在這樣的規(guī)律。

師：誰能舉幾個(gè)例子進(jìn)行驗(yàn)證？

（學(xué)生舉例，教師板書）

師：（54×0）÷（18×0）和（54÷0）÷（18÷0）這兩個(gè)例子行嗎？難道前面的規(guī)律錯(cuò)了？

（學(xué)生討論交流，得出完整的商不變的規(guī)律）

在學(xué)生思維斷層處，教師順勢“引”思：“老師也來舉兩個(gè)例子”，適時(shí)將“0”這一特殊情況納入，豐富了學(xué)生的探索空間，引導(dǎo)學(xué)生改變思維方式，讓探索更全面，更完善，更深刻。

三、引思，“引”在智慧碰撞處

引思的目的，是為了促進(jìn)學(xué)生的發(fā)展。課堂教學(xué)中，不同學(xué)生對知識(shí)的理解處于不同層次，有的清晰，有的模糊；有的真實(shí)有效，有的也許徒勞無益。教師應(yīng)抓住問題的本質(zhì)，準(zhǔn)確“引”思，既讓不同的學(xué)生經(jīng)歷思維，體驗(yàn)學(xué)習(xí)的樂趣，也不讓課堂教學(xué)航向走偏，真正發(fā)揮教師的主導(dǎo)作用。

【課例3】“分?jǐn)?shù)的意義”教學(xué)片斷

課件出示圖示：

圖1　

師：如圖1，第1行四個(gè)餅看作單位“1”，第二行用哪個(gè)數(shù)表示？第三行呢？第四行呢？

圖2　

師：如圖2，第2行的兩個(gè)餅看作單位“1”，第一行用哪個(gè)數(shù)表示？第三行呢？第四行呢？

圖3　

師：如圖3，第三行的1個(gè)餅看作單位“1”，第一行用哪個(gè)數(shù)表示？第二行呢？第四行？

圖4　

師：如圖4，剛剛的三種情況放在一起，什么是不變的？（餅的數(shù)量）什么是變化的？（單位“1”）

這里，教師為學(xué)生提供了開放的、極具挑戰(zhàn)性的平臺(tái)，讓學(xué)生的思考有方向，思維更完整。

作為課堂教學(xué)的引導(dǎo)者，教師要智慧地處理“讓學(xué)”與“引思”的關(guān)系，教師要適時(shí)“引”、有效“引”、智慧“引”，這樣的課堂才會(huì)真正實(shí)現(xiàn)以生為本的目標(biāo)。

（責(zé)編金鈴）

G623.5

A

1007-9068（2016）29-006