邂逅拐點設置障礙，讓學生的思維多飛一會兒

江蘇濱海縣實驗小學（224500）　徐榮書

邂逅拐點設置障礙，讓學生的思維多飛一會兒

江蘇濱海縣實驗小學（224500）徐榮書

在小學數學教學中，當學生思維遇到拐點時，教師要做的就是提供空間和時間，搭建平臺，讓學生充分思考和自主探索，幫助學生形成反思、質疑等數學思維能力。

小學數學教學策略發展思維最近發展區

在小學數學教學中，當學生位于最近發展區，已有知識和新知之間進行遷移時，將會面臨三個思維的拐點：概念易混點，思路盲動點，方法構建點。此時，教師要做的就是提供充足的空間和時間，在拐點處設置障礙，帶領學生經歷知識形成的過程，培養學生的思維能力。

一、在概念易混點設置障礙，讓思維多飛一會兒

很多數學概念和定理法則是數學學習的基礎，在進行這些基礎建構的時候，如果有一點點錯誤，都容易為進一步學習帶來阻礙。因此，教師可以圍繞思維拐點設置一些障礙，引發學生自主思維，通過比較、辨析等多種活動，深化學生對數學概念、公理、法則等知識的建構。

比如，在教學三角形的分類時，為了讓學生能夠直觀理解銳角三角形、鈍角三角形和直角三角形，筆者用多媒體向學生呈現3個三角形當中的某一個角，讓學生判斷這3個三角形分別是什么三角形：

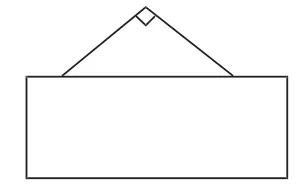
圖1　

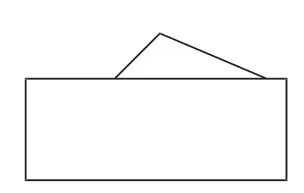
圖2　

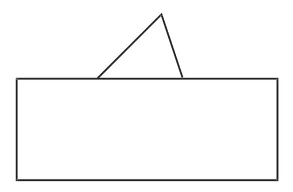
圖3　

對圖1和圖2，學生能夠很快判斷出三角形分別為直角三角形和鈍角三角形，而在圖3中，學生不假思索地判斷三角形為銳角三角形。此時我故意設置障礙：“真的確認是銳角三角形嗎？說出你的理由。”學生逐步認識到：判斷一個三角形是否是銳角三角形，只根據露出的一個銳角是不能確定的，而是需要知道這3個角是否都是銳角。由此，學生對銳角三角形有了清晰的認識。在這個教學過程中，學生提出了新的問題：為什么有一個角是直角的三角形一定是直角三角形？有一個角是鈍角的三角形一定是鈍角三角形嗎？根據學生的疑問，我繼續引導：“每個三角形至少有兩個銳角嗎？可能與三角形的什么有關？”學生的思維被逐步打開，為進一步的學習奠定了基礎。

以上環節，教師圍繞學生的思維拐點，通過數學障礙的設置，幫助學生在嘗試和比較中鞏固了銳角三角形的特點，為學生后繼學習建立起積極的心理狀態。

二、在思路盲動點設置障礙，讓思維多飛一會兒

由于年齡小，學生在解決問題時常常會陷入思維混沌的盲動狀態。此時，教師要緊緊抓住思維的拐點，精心設置障礙，幫助學生消除盲動點。

比如，應用題：小麗將自己積攢的畫片的一半還多6張送給了小冉，還剩下24張。請問小麗原來有多少張畫片？學生列出算式：24÷2+6；24÷2-6；24×2-6，（24+6）÷2……從這些解答方式不難看出，由于受到定式思維的影響，學生看到題目中有“一半”這個詞，就產生了要除以2的盲動思維；有的看到“還多”這個詞，就產生了要用加法的盲動思維。由于沒有設定的目標，數量關系不夠清晰，因而給學生帶來了很多困擾。基于此，我設置了如下障礙：小麗原有的畫片比24張多還是少？為什么？如果小麗將自己畫片的一半還多6張送給小冉，還剩下的比一半多還是比一半少？畫片的一半正好是多少張？通過解決這些問題，學生學會運用倒推的方法進行分析，從而找到解決的辦法。

教師在學生的思路盲動點處設置障礙，讓學生的思維多飛一會兒，幫助學生克服了定式思維所造成的負遷移，大大提升了學生解決問題的能力。

三、在方法構建點設置障礙，讓思維飛一會兒

在小學數學教學中，教師要引導學生構建問題解決的方法，這個構建點正是思維的拐點。此時，教師要緊扣這個方法點設置障礙，帶領學生進行比較和深入探究。

比如，習題：要將一張長48厘米、寬32厘米的長方形紙裁成長為6厘米、寬為4厘米的小長方形紙片，最多能裁多少個？不少學生用“總面積÷每個小長方形的面積”，列出算式“48×32÷（6×4）=64（張）”。此時我設置了障礙：將寬為32厘米改為29厘米。學生還按照之前的辦法列式“48×29÷（6×4）=58（張）”。我畫出圖4，并追問：“這樣能正好裁完而沒有剩余嗎？對比兩道題，看看如何解決？”學生發現，原有方法并不能對所有條件都適合，需要考慮余下的能不能繼續裁，由此列出算式“29÷4=7（個）……1（厘米），48÷6×7=56（張）”。

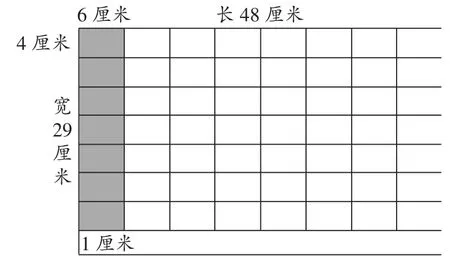
圖4　

教師在方法構建點設置障礙，帶領學生在沖突中生成新的解決方法，發展了學生的數學能力。

總之，在小學數學教學中，教師要抓住有利時機設置障礙，讓學生的思維多飛一會兒。

（責編童夏）

G623.5

A

1007-9068（2016）29-090