關(guān)于正項級數(shù)收斂性判別法的幾點說明

鄧小宇

（貴州財經(jīng)大學，貴州貴陽550025）

關(guān)于正項級數(shù)收斂性判別法的幾點說明

鄧小宇

（貴州財經(jīng)大學，貴州貴陽550025）

由于正項級數(shù)收斂性的判斷方法較多，學生掌握起來比較困難。因此，文章就正項級數(shù)收斂性判別的幾種方法作幾點簡要的說明，幫助學生解決在做題過程中存在的一些問題。

正項級數(shù)；比較判別法；比較判別法的極限形式；比值判別法

正項級數(shù)收斂性判別法是高等數(shù)學中無窮級數(shù)的一個重點和難點。但是，由于正項級數(shù)收斂性的判斷方法較多，判斷正項級數(shù)收斂時，學生總是難以選擇合適的方法進行判斷。因此，文章就正項級數(shù)常用的幾種收斂性判斷方法，做幾點說明。

一、正項級數(shù)的比較判別法

選擇正項級數(shù)判別法時，應(yīng)滿足以下條件：

1.正項級數(shù)的通項應(yīng)該容易放大或容易縮小。

2.放大或縮小后的通項構(gòu)成的正項級數(shù)應(yīng)當是常見的調(diào)和級數(shù)、等比級數(shù)或P-級數(shù)，或者該級數(shù)的收斂性是比較容易判斷的。

3.放大后的通項構(gòu)成的正項級數(shù)必須為收斂的正項級數(shù)，縮小后的通項構(gòu)成的正項級數(shù)必須為發(fā)散的級數(shù)。

二、正項級數(shù)的比較判別法的極限形式

1.選作用于比較的已知級數(shù)一般為等比級數(shù)或P-級數(shù)。一般情況下，當正項級數(shù)通項中變量n位于冪指函數(shù)的指數(shù)位置時，選擇等比級數(shù)與之作比較；當正項級數(shù)通項中變量n的位置出現(xiàn)在冪指函數(shù)的底數(shù)位置時，選擇P-級數(shù)與之作比較。

2.當正項級數(shù)的通項是n→∞時的無窮小量，而其等價無窮小量又容易找到，則可通過等價無窮小量關(guān)系找到與之作比較的已知級數(shù)。

三、正項級數(shù)的比值判別法

一般情況下，當正項級數(shù)的通項中含乘積因子n！或an時，可

選擇比值判別法。此時，根據(jù)比值判別法的判斷依據(jù)該極限值會比較容易求解。

解：因為通項中含有n！和3n的乘積因子。因此，選擇比值判別法，即：

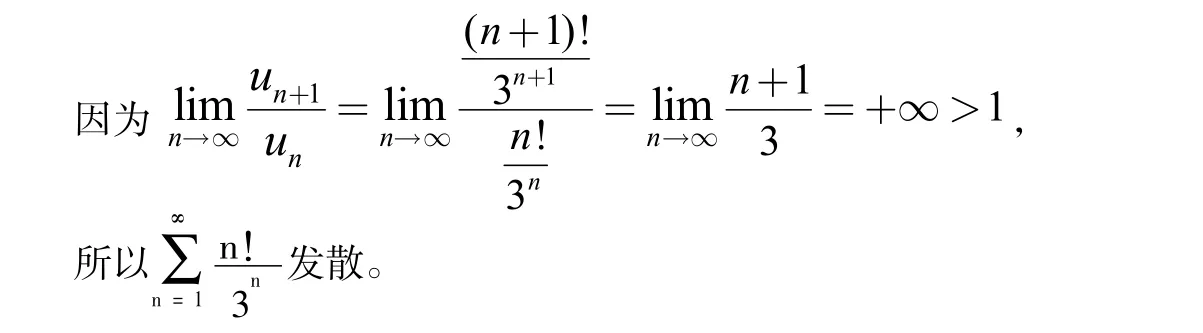
有時對于一個正項級數(shù)收斂性的判斷，方法可能不止一個。此時，選擇比較簡單的一種判別法。而有時對于一個正項級數(shù)收斂性的判斷，往往需要幾種判別方法的綜合運用。

正項級數(shù)收斂性的判斷題型靈活多樣，在這里我們不能窮盡其所有題型。學生只能是多做題、多思考、多總結(jié)，才能掌握好正項級數(shù)收斂性的判斷方法。

［1］吳傳生.經(jīng)濟數(shù)學——微積分［M］.高等教育出版社，2014.

［2］同濟大學數(shù)學系.高等數(shù)學［M］.高等教育出版社，2011.

It is difficult for students to grasp so many convergence of positive series test.Therefore，this paper briefly introduces several methods of positive series of convergence criterion，to help students solve some problems that exist in the study.

series of positive terms；comparative judgment method；the limit form of comparative judgment method；the ratio test

O13

A

2096-000X（2016）22-0263-02

鄧小宇（1978，11-），女，貴州畢節(jié)市人，貴州財經(jīng)大學數(shù)學與統(tǒng)計學院，副教授，研究方向：數(shù)學教育。