微積分在高中數學中的應用研究

貴州工程應用技術學院 曹發勇

微積分在高中數學中的應用研究

貴州工程應用技術學院 曹發勇

微積分在高中數學中占據著非常重要的作用，對培養學生的邏輯思維能力、想象能力和創新能力能夠發揮重要的作用。本文針對高中數學中的關于極限、導數等難點，探討微積分在解決這些難點中的應用方法，對微積分在高中數學的應用做出有益的思考。

微積分；高中數學；應用

微積分是數學科學的重要組成部分，由17世紀牛頓和萊布尼茨分別創立。微積分在描述變量和函數中起到了非常重要的作用。新《普通高中數學課程標準》中對微積分的教學內容進行了改革，通過在高中階段使學生初步了解微積分的思想，為學生進入大學階段學習高等數學打下良好的基礎。本文通過例子，說明微積分在求解極值、函數單調性、方程求解等方面的應用。

一、利用微積分求解函數極值

微積分在求解函數極值中有著非常巧妙的應用。求解步驟為：（1）首先對函數f（x）求導f'（x）；（2）求解方程f'（x）=0的根；（3）判斷f'（x）在f'（x）=0根的兩邊的符號，確定極值的類型。

解：f'（x）=lnx+1=0，可得x=1/e，而當x位于（0，1/e）時，f'（x）＜0，f（x）為減函數；當x位于（1/e，e］時，f'（x）＞0，f（x）為增函數。

可知：x=1/e，f（x）取極小值，f（x）取值為-1/e；當x=e時，取極大值，f（x）取值為e。

利用函數求導可以迅速判斷出函數的極值。

二、利用微積分判斷函數的單調性

函數單調性的判斷是高中數學中一個非常重要的內容，也是歷年高考重要的考點。利用函數求導后的正負，很容易判斷出函數的單調性。

例2：（2009年廣東卷文）函數f（x）=（x-3）ex的單調遞增區間是（ ）。

A.（-∞，2） B.（0，3） C.（1，4） D.（2，+∞）

分析：對函數f（x）求導，f'（x）＞0的解即為單調遞增區間。

f'（x）=ex+（x-3）ex=（x-2）ex＞0，可得x＞2。因此，本題選D。

三、利用微積分求證不等式

利用導數研究函數的單調性，再由單調性來證明不等式是函數、導數、不等式綜合中的一個難點，也是近幾年高考的熱點。其主要思想是構造輔助函數，把不等式的證明轉化為利用導數研究函數的單調性或求最值，從而證得不等式。

例3：當x位于（0，π）時，證明不等式sinx＜x成立。

分析：構建函數f（x）=sinx-x，對其求導，并判斷導數的正負即可。

構建函數f（x）=sinx-x，求導可得f'（x）=cosx-1

由于x位于（0，π），因此f'（x）＜0。

因此f（x）=sinx-x在區間（0，π）上為單調減函數，而f（x）=0，

因此在x位于（0，π）時，f（x）＜0，

即sinx＜x成立。

四、利用微積分求解曲面面積

定積分是新課標中新加的內容，新《課標》對定積分的定位如下：（1）通過求曲邊梯形的面積、變力做功等實例，從問題情境中了解定積分的實際背景；借助幾何直觀體會定積分的基本思想，初步了解定積分的概念，為以后進一步學習微積分打下基礎；（2）通過實例，直觀了解微積分基本定理的含義；（3）了解微積分的文化價值。可見，高中課程學習積分與定積分，重在粗淺地領略其主要思想和基本方法，從一些實例中初步認識定積分的工具作用。近年來，部分地區高考主要在定積分的求法、定積分的簡單應用尤其是利用定積分求面積上做文章。

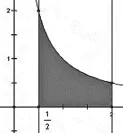
例4：（2008海南、寧夏卷理）由直線x=0.5，x=2，曲線y=1/x及x軸所圍圖形的面積是（ ）。

A.15/4 B.17/4

C.0.5ln2 D.2ln2

分析：此題是求連續曲線y=1/x，x軸二直線x=0.5，x=2，所圍成的曲邊梯形的面積。

五、利用微積分在數列問題中的應用

例5：求數列1，2x，3x2，…，nxn-1的和（其中x≠0，x≠1）。

分析：這道題可以用錯位相減法求和，但若用導數方法運算會使問題更加簡明。

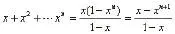
六、小結

微積分能夠高速有效地解決很多數學問題，在高中數學中也有著廣泛的應用。微積分自進入高中數學以來，對培養學生的數學思維方式提供了新的途徑，也為幫助學生在進入大學后更好地學習微積分打下良好的基礎。微積分在高中數學中有著廣泛的應用，除了本文上述的領域之外，在方程求根、函數圖像、切線方程和面積求解等領域也有著廣泛的應用，值得進一步去探討研究。

［1］許榮良.高中數學解題中微積分的應用［J］.數理化學習（高中版），2014（11）.

［2］張海燕.微積分在高中數學解題中的應用［J］.中學生數理化（學研版），2015（8）.

［3］王湘平.微積分在高中數學解題中的應用［J］.才智，2013（5）.

曹發勇（1991- ），男，貴州赫章人，漢族，本科學歷，學士學位，數學與應用數學專業。）