如何通過函數的單調性解決參數取值范圍的問題

江蘇省溧陽市埭頭中學 王麗萍

如何通過函數的單調性解決參數取值范圍的問題

江蘇省溧陽市埭頭中學 王麗萍

利用函數的單調性，求參數的取值范圍問題，是學生比較棘手的問題，但也并不是無法可循，下面就幾個簡單的例題來闡述一下個人的觀點。

方法一：利用一元二次函數根的大小情況判斷函數的單調性，其實就是利用函數的單調增區間D與函數在某一區間I上單調增之間的關系解決問題。

方法二：分離變量法。這種方法要注意在分離變量的過程中不等號的方向是否要改變，最后轉化成求函數的最值問題。

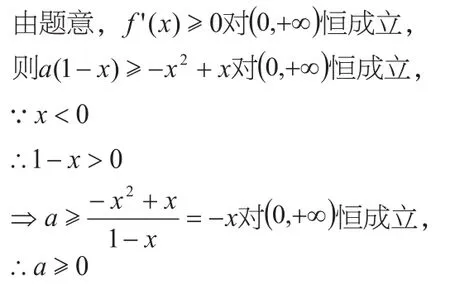
但是有的時候函數的導函數雖然是一個一元二次函數，卻不能因式分解。例如：

像這里的一元二次函數，就不能像上述例題一樣，簡單地通過因式分解求得函數的單調區間去解決問題，即使要求單調區間，也要通過求根公式，過于復雜。但是可以利用研究一元二次函數的對稱軸與區間的位置關系，判斷端點值的取值情況來解決問題。

故a≥1。

通過上述兩個例題，我們可以發現對于研究已知某一三次函數在某區間上的單調性，求參數的取值范圍問題，常見方法是兩種。方法一：利用它的導數是一元二次函數這一特征，結合一元二次函數的有關性質，即區間根問題，解決問題。但這里面的處理方法有很多種，而這又恰恰是學生學習過程中的一個盲點，學生經常會考慮得不全面，從而影響最后的計算結果。方法二：分離變量法，這種方法還是具有一般性的。……