例談計算教學中算法的有效建構

江蘇省東臺市東臺鎮四灶小學 申碗平

例談計算教學中算法的有效建構

江蘇省東臺市東臺鎮四灶小學 申碗平

計算教學是小學數學教學的重要部分，在平時的計算教學中，教師常常忙于演示與講解，忽視學生參與建構算法的心理歷程。學生對算法的掌握僅僅停留在記憶與模仿上，學生不明白為什么這樣算，為后繼的學習埋下了很大的隱患。本文更關注學生建構算法的內部機制，試圖結合一些實例談談如何更有效地幫助學生理解算理、掌握算法。

問題情境；表象操作；題組

筆者認為，要提升計算教學的有效性，教師要充分利用好結構化的問題情境，要合理搭建理解抽象算理的平臺，要最大化地發揮題組功能。下面筆者結合蘇教版三年級上冊第一單元“除法”的教學談談計算教學中算法的有效建構。

一、充分利用結構化的問題情境，為理解算理、構建算法提供直觀的幫助

問題情境的結構性是指問題情境的構建及其發展揭示的知識應有內在的邏輯結構。我們知道，結構化知識是最易于轉化為認知結構的，而結構化的情境則為這種轉化提供了心理空間，能促進這種轉化，能夠有效激發學生的問題意識和策略意識，激活學生的數學思維。教材從學生的最近發展區出發，精心設計數學問題情境的呈現方式，努力發揮數學問題情境的導向作用，促使學生親身經歷將實際問題抽象成形式化數學知識的過程，進而獲得對有關概念、法則、性質和規律的理解，發展數學能力，增強問題意識和數學應用意識。因此，在計算教學中要十分重視引導學生觀察情境圖中具體的學習對象，發現有價值的信息，為理解算理、構建算法提供直觀的幫助。

例如，教學三年級（上冊）“兩位數除以一位數的除法”時，教材創設了同學們買鉛筆的問題情境，先教學整十數除以一位數的口算，再教學兩位數除以一位數的筆算。

由于是第一次接觸這樣的口算和筆算，教材精心設計了問題情境的呈現方式，在以對話的方式呈現有關信息的同時，還出示了相應的鉛筆圖。圖中的“4捆鉛筆”即4個十和“4捆又6支鉛筆”即4個十6個一，對口算和筆算的計算思路都有很好的暗示作用。在口算時，根據“4捆”的鉛筆圖，學生容易想到“把40支鉛筆平均分給2個小朋友，就是把4捆鉛筆平均分成2份，每份是2捆，是20支”。在筆算時，根據“4捆又6支”的鉛筆圖，學生容易想到把46支鉛筆平均分給2個小朋友，可以先分整捆的，再分單根的；也可以結合上面學習的口算，想到“40÷2=20，6÷2=3，20+3=23”。兩種思路都隱含著“先用兩位數十位上的數除以一位數，再用個位上的數除以一位數的方法”。這就為進一步探索筆算方法提供了十分豐富的感性經驗，為學生的自主探索提供可能，使學生“跳一跳”就能“摘到果子”。

二、充分利用表象操作，為計算方法的抽象搭建平臺

著名教學心理學家布魯納的“表象認識論”指出，兒童的認知水平應經歷三個階段，即行為表征、表象表征、符號表征。也就是說兒童的學習應該從感知操作到形成表象再到形成形式化的符號表達。在由直觀操作過渡到一般算法的過程中，需要重視表象操作這一中間環節。所謂表象操作，就是在具體實物操作的基礎上，教師引導學生聯系實物操作的方法和過程，在頭腦中進行類似的操作。這樣可以幫助學生擺脫具體實物的束縛，更好地構建比較抽象的算法。如果跳過這一環節，學生的算法構建容易與直觀操作相脫節。

例如，教學三年級（上冊）“首位不能整除的兩位數除以一位數的筆算除法 ”的內容。主題畫面中有5桶羽毛球和2個羽毛球，要求平均分給2個班，每班能分到多少個？學生很容易想到算式52÷2，學生嘗試計算受挫。這時，教師不應急切板演講解，應有序列地帶領學生開展探索“52÷2=？”的活動。

第一層次，以實際動手操作積累表象操作的經驗。教師課前準備5桶羽毛球和2個羽毛球，讓學生動手分一分。當學生分整桶時，出現5桶不能正好分掉的問題，于是學生想到了“拆整桶”（這其實就是“退一當十”的數學原型），進而明白分單個的時候，不只是分畫面中的2個，還有1桶里的10個，合計12個。在操作中他們能先分給每班2筒，再把余下的1筒羽毛球和另外2個合起來繼續平均分。反復操作幾次之后，進入表象操作。

第二層次，以表象操作的經驗推進算法的建構。讓學生脫離開羽毛球實物，動腦想把52個羽毛球平均分給2個班是如何操作的。（52÷2）學生在腦中表象出“分整桶”“拆整桶”“分單個”，進而將“分的過程”在頭腦中數學化，實現實物單位“桶”“個”向計數單位“十”“個”的轉變，最終實現由“分52個羽毛球”到“分52這個數”的思維跨越，明白被除數十位上余的是1個“十”，可以和個位上的2合成12繼續除，突破學生思維瓶頸。進而形成“首位不能整除的兩位數除以一位數的筆算除法”的計算方法：計算“52÷2”時要先算40÷2=20，再算12÷2=6，合起來就是26。在此表象操作基礎上，學生聯系豎式的寫法和已有的計算過程，容易完成并理解以下的豎式。

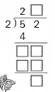
第三層次，由抽象的算法“反”想表象操作的過程。豎式形成后，引導學生思考：“豎式中的4是什么意思？”“豎式中5減4得1，這個1表示什么意思？”“商十位上的2是怎么得到的？商個位上的6又是怎么得到的？”通過“反”想活動，進一步幫助學生內化計算原理，使學生真正“摘到果子”。

［1］侯正海.在理解算理的基礎上構建算法［J］.小學數學教學網，2010.

［2］楚平.問題情境——計算教學的活力源泉［J］.小學數學教學網，2011.