亞軌道飛行器發動機故障下配平能力分析

王文虎， 韓冰

中北大學 機電工程學院， 太原 030051

亞軌道飛行器發動機故障下配平能力分析

王文虎*， 韓冰

中北大學 機電工程學院， 太原 030051

為了分析亞軌道飛行器發動機故障下配平能力，將配平能力問題轉換為線性等式/不等式混合方程組相容性判定問題。提出了將基于頂點投影法的相容性判定方法用于配平能力分析，驗證了方法的準確性與計算效率。在故障下配平能力分析的總體框架下，分別對不同故障模式下故障發生時刻、整個空域配平能力進行分析，給出了配平能力不足時的應急策略。仿真結果表明，該方法能夠快速地計算故障下不可配平區域、分析配平能力對可飛區域的影響，對故障后任務中止策略、任務中止軌跡優化等研究具有重要的參考價值。

亞軌道飛行器； 發動機故障； 配平能力； 相容性判定； 混合方程組

發動機是亞軌道飛行器(Suborbital Reusable Launch Vehicle, SRLV)較易發生故障的關鍵部件[1-3]。SRLV發動機故障下，快速有效地判斷故障飛行器的控制配平能力對飛行安全至為重要。

亞軌道飛行器上升段控制的執行機構為擺動發動機[4]，若發生故障，必然會造成控制力矩的損失，嚴重情況下可能導致控制配平能力不足，影響飛行任務的安全性。有必要根據故障模式、當前的飛行狀態，判斷是否能夠配平、分析配平不足時的應急策略及配平能力下降對飛行約束的影響。因此，配平能力分析也是故障下任務中止決策的重要依據之一[5]。

針對重復使用運載器執行機構故障下配平能力問題，國內外學者進行了相關的研究。美國海軍研究生院Ross與空軍研究實驗室Doman等對X-33進場著陸段氣動舵面故障下容錯最優軌跡進行了研究，并通過配平能力分析將故障對六自由度模型的影響引入至三自由度模型中[6-9]。西北工業大學解永鋒采用非線性控制分配算法進行了SRLV返回段氣動舵面故障下配平特性計算[10]。文獻[11-13]采用可變單純形法、線性規劃法、序列二次規劃方法進行配平能力分析。本質上，上述方法均為基于數值優化的方法，這類方法容易收斂到局部最優解，同時求解時間也相對較長。

本文首先通過簡化，將SRLV配平能力問題轉化為線性等式/不等式混合方程組相容性判定問題，提出了基于頂點投影法的相容性判定方法用于配平能力分析。然后，給出了SRLV發動機故障下配平能力分析總體框架，并針對不同故障模式從故障發生時刻配平能力分析和整個空域配平能力分析2個方面進行了研究。

1 SRLV配平問題描述與簡化

1.1 配平問題描述

圖1 SRLV發動機配置示意圖Fig.1 Schematic diagram of SRLV engine arrangement

為實現飛行器的轉動配平，雙擺發動機產生的力矩ME與氣動舵產生的力矩MA之和必須抵消掉機體產生的期望配平的氣動力矩Mdes。

通過推導可得，ME在體坐標系各軸上的分量即滾動、偏航、俯仰力矩為

(1)

式中：

式中：P1、P2分別為1#、2#發動機的推力大小；rc為發動機鉸鏈位置至SRLV縱向對稱平面xbobyb的距離。

MA、Mdes可由氣動力矩公式得到，均與動壓、馬赫數、攻角等有關，并且在這些飛行狀態已知的情況下，氣動舵面操縱力矩MA是舵偏角δe、δr、δa和δbf的非線性函數。

令發動機擺角/氣動舵偏角向量

(2)

且δ的擺動極限位置向量分別為δmax、δmin。則判斷能否配平可描述為是否存在發動機擺角/氣動舵偏角向量δ，使得滿足

(3)

可見，在其他飛行狀態給定的情況下，式(3)為關于δ的有約束非線性方程組。

配平問題本質上是一個控制分配問題。由于SRLV發動機擺角/氣動舵偏角個數大于受控變量即操縱力矩(俯仰、偏航和滾轉通道力矩)的個數，故存在一定的控制冗余度，可以由控制分配算法求解。控制分配算法在給定性能指標的前提下，不僅能夠檢驗飛行器能否配平，還能給出發動機擺角的最優組合。但常見的控制分配算法都是基于優化的，計算時間較長，并且算法的誤差也可能導致配平能力的誤判。本文的配平能力分析只期望能夠在發生故障下快速地判斷飛行器能否配平。因此，可通過判斷式(3)解的存在性來檢驗飛行器能否配平。若式(3)有解，則飛行器能夠配平，反之則不能配平。

1.2 配平問題簡化

由于主發動機噴管擺動角度較小(±10°以內)，為便于分析計算，可取

(4)

考慮到氣動數據離散的存儲在多維插值表中，因此可利用原始氣動數據，將舵面氣動力矩與舵偏角之間存在的非線性關系進行分段線性化。

假定分段線性化后舵偏角分段組合個數為K，則對第k個舵偏角分段組合，式(3)可簡化為

(5)

(6)

式中：BAk為第k分段氣動舵效率矩陣；δkmin、δkmax為第k個分段擺角/氣動舵偏角極限位置，可根據發動機擺角位置約束與原始氣動數據分段情況得到。且有

(7)

式中：Mx、My和Mz分別為機體產生的滾動、偏航和俯仰氣動力矩，即Mdes在體坐標系下的分量。

在分類算法方面,本文對比了GMM算法,支撐矢量機(SVM)和BP神經網絡(ANN)算法。實驗仍然采用K-交叉驗證法,實驗結果如圖5所示。由圖5可知,3種算法中,GMM算法的效果最佳,最差的神經網絡算法。SVM算法本身對于多分類問題的效果不佳,而ANN算法對網絡結構的要求較高,因此基于概率的GMM算法的有效性更好。

至此，配平能力分析問題轉化為如式(5)所示線性等式/不等式混合方程組相容性判定問題。若K個分段中只要存在1個分段使式(5)有解(相容)，則飛行器能夠配平，否則不能配平。

配平問題的簡化是將問題線性化的過程。為使該方法更具實際工程應用價值，發動機噴管擺動角度越小、氣動數據離散點越密，越能滿足線性化條件。考慮到現有運載火箭二級以上基本采用帶小噴管的游動發動機控制飛行姿態，小噴管最大擺角可達60°，線性化條件不能滿足。因此，本文方法不適用于采用游機控制的重復使用運載器。

2 基于頂點投影法的相容性判定方法

為了與本文研究內容相對應，考慮如下形式線性等式/不等式混合方程組

(8)

式中：A的元素為aij(i=1,2,…,m;j=1,2,…,n)；b=(b1,b2,…,bm)T；x=(x1,x2,…,xn)T；xl=(x1l,x2l,…,xnl)T；xu=(x1u,x2u,…,xnu)T。

若要判斷該方程組的相容性，一種思路是先將線性等式/不等式方程組轉化為線性不等式方程組，然后通過判定線性不等式組圍成的凸空間是否為空來進行相容性判定。判定線性不等式組圍城的凸空間是否為空可通過交邊算法、位置算法或梯度算法進行求解[16-18]，但這類方法需要先將線性等式方程組轉化為不等式方程組，會降低計算效率。

本文提出一種新的基于頂點投影法的線性等式/不等式方程組相容性判定方法。該方法不需要將等式方程轉化為不等式方程，根據線性等式方程組解的形式對問題分類處理，通過n維線性空間中，點到超平面投影及超長方體頂點與其投影點構成的空間向量等手段判斷超平面與超長方體的空間位置關系，從而對線性等式/不等式方程組相容性進行判定。

令集合S={x|Ax=b,x∈Rn}，則當S不為空時，表示由Ax=b所確定的n維線性空間的點、直線或超平面。令集合D={x|xl≤x≤xu,x∈Rn}，則D表示n維空間內某一超長方體(D≠?)。若S∩D≠?，則式(8)相容(有解)，否則不相容(無解)。

為了便于理解算法流程，先對n維線性空間點到超平面投影計算方法及通過超長方體頂點與其投影點構成的空間向量判斷相容性等問題進行探討。

1)n維線性空間點到超平面投影計算方法

若線性等式方程組Ax=b所確定的超平面為S，假定n維線性空間內任意一點為x0=(x10,x20,…,xn0)T。若需求點x0在超平面S內的投影點，則令超平面內一點x與x0間距離d最短，有

(9)

而Ax=b可視為線性等式約束，則令

(10)

式中：λi為拉格朗日乘子。則由極值條件可得

(11)

由式(11)可得

(12)

將式(12)代入Ax=b，令λ=(λ1,λ2,?λm)T可得

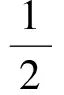
(13)

則有

λ=2(AAT)-1(Ax0-b)

(14)

代入式(12)得

x=x0-AT(AAT)-1(Ax0-b)

(15)

注意到當A不為行滿秩情況下，(AAT)-1不存在。為使方法適用于任意矩陣A，引入廣義逆矩陣概念，即有

x=x0-AT(AAT)+(Ax0-b)

(16)

對于加號逆，有性質A+=AT(AAT)+，故x0在超平面S內的投影點x為

x=x0-A+(Ax0-b)

(17)

該方法不需要求解方程組Ax=b，可直接由式(17)計算得到n維線性空間點到超平面投影坐標。

2) 相容性判定準則及其證明

相容性判定準則：設超長方體D的頂點為Zk(k=1,2,…,2n)，任取一頂點Zk，其在超平面S上的投影為P，P與所有頂點構成的向量為Wk=PZk(k=1,2,…,2n)。若除Wk外所有空間向量W1,W2,…,Wk-1,Wk+1,…,W2n中只要有一個使得其與向量Wk的內積小于或等于零，則超長方體D與超平面S相交，即S∩D≠?。否則，S∩D=?。這條判定準則也適用于任意凸多面體。

證明：

(18)

則有

[Wk,Wl]=[Wk,WPQ+WQZl]=

[Wk,WPQ]+[Wk,WQZl]≤0

(19)

當Zk與其投影點P重合時，Zk與P構成的向量Wk=0，有[Wk,WPQ]=0；當Zk與P不重合時，Wk為超平面S的法向量，而P與Q點均在超平面S內，故有Wk⊥WPQ，即[Wk,WPQ]=0。由式(19)可知：[Wk,WQZl]≤0。可分兩種情況考慮：

① [Wk,WQZl]=0

當[Wk,WQZl]=0時，可得Wk=0或WQZl=0或Wk⊥WQZl。若Wk=0或WQZl=0分別可得超長方體頂點Zk或Zl在超平面S內，則S∩D≠?。若Wk⊥WQZl，而Q點在超平面S內，則Zl必在超平面S內，故S∩D≠?。

② [Wk,WQZl]<0

當[Wk,WQZl]<0時，Wk、WQZl均不為0且方向相反，P與Q均為投影點，而Wk、WQZl為超平面S的法向量，因此超長方體頂點Zk與Zl必在超平面S的兩側，可得超平面S必與超長方體D相交，即S∩D≠?。

綜上所述，當[Wk,Wl]≤0時，S∩D≠?。

證畢.

圖2 相容性判定準則示意圖Fig.2 Schematic diagram of compatibility decision criterion

2.2 算法流程

圖3給出了基于頂點投影法的線性等式/不等式混合方程組相容性判定流程，具體算法如下：

圖3 相容性判定流程圖Fig.3 Flowchart of compatibility decision

1) 判斷S是否為空

2) 判斷S是否為超平面

若rankA≥n-1，求解線性方程組Ax=b。當rankA=n時，Ax=b存在唯一解x*，判斷x*是否在集合D內，若x*∈D，則等式/不等式方程組相容，否則不相容，程序返回。當rankA=n-1時，Ax=b有無窮多解，通解為x*=η*+kξ(k∈R)，ξ為齊次線性方程組Ax=0。判斷其特解η*是否在集合D內，若η*∈D，則等式/不等式方程組相容，程序返回；否則，令xl≤x*≤xu，則可得xl≤η*+kξ≤xu，這是一個關于實數k的不等式方程組，可通過不等式性質求解，若該不等式方程組相容，則等式/不等式方程組相容，否則不相容，程序返回。

若rankA

3) 判斷S是否與超長方體D相交

通過已證明的相容性判定準則判斷S是否與超長方體D相交，若相交則等式/不等式方程組相容，否則不相容，程序返回。

2.3 相容性判定計算效率

為了驗證所提出方法的計算效率，針對不同規模線性等式/不等式混合方程組，分別采用單純形法、交邊算法及本文提出的方法進行了相容性判定。

表1為相容性判定方法計算效率比較結果。可以看出，對于較大規模問題，本文方法也能快速地對問題的相容性進行判定，計算效率要高于單純形法及交邊算法。

表1 方法計算效率驗證Table 1 Verifying method’s efficiency

3 SRLV發動機故障下配平能力分析

3.1 故障下配平能力分析總體框架

為使讀者對后面內容有一個全局了解，圖4給出了故障下配平能力分析的總體框架。

圖4 配平能力分析總體框架Fig.4 Framework of trim capacity analysis

主要從2個層面對故障下配平能力進行分析，包括：故障發生時刻配平能力分析和整個空域內配平能力分析。

故障發生時刻配平能力分析是利用故障發生時刻飛行狀態對當前飛行器控制配平能力進行分析，目的是在控制能力不足時快速做出應急策略。正常飛行上升段采用擺動發動機單獨控制，在給定故障模式與故障發生時刻條件下若不能配平，則采用發動機/氣動舵復合控制策略，若復合控制仍不能配平，則需要采取某些配平不足應急策略以滿足控制配平需求。若故障下兩種控制策略能夠實現配平，則表明故障點附近飛行器具有控制配平能力，但不代表在整條飛行軌跡上能夠配平，由于故障可能會導致飛行軌跡與正常飛行情況有較大變化，因此有必要對故障下整個空域內配平能力進行分析。

整個空域內配平能力分析是針對不同故障模式對選定的飛行狀態區域內所有點進行控制配平能力進行分析，目的是分析由于故障引起的配平能力下降對飛行包絡及飛行約束的影響。

因此，故障發生時刻配平能力分析可看作為一種短時效的配平能力分析，只對當前狀態附近點有效，可為故障時刻控制能力分析提供參考；整個空域內配平能力分析可看作為一種長時效的配平能力分析，對故障后整個飛行軌跡上狀態點均有效，可為故障后任務規劃、軌跡重構及制導等提供依據。

3.2 故障發生時刻配平能力分析

1) 正常飛行情況

為便于后面故障下配平分析并驗證提出的判定方法，圖5給出了正常飛行情況有動力上升段攻角α、馬赫數Ma、飛行高度H、動壓q等狀態隨飛行時間t變化曲線，同時利用提出的方法對無故障下正常飛行軌跡上各飛行時刻進行配平分析，結果表明不同飛行時刻均能夠實現配平，單個數據點平均配平計算速度在10-4s量級。

2) 單臺發動機推力損失情況

若單臺發動機發生故障，則故障發動機推力的下降以及由于故障后兩臺發動機推力不相等導致的不對稱力矩都會對控制配平能力造成影響。圖6給出了1#、2#發動機不同推力損失比例Rp下，不同故障發生時刻tF，發動機單獨控制上升段配平能力分析結果。

圖5 正常飛行有動力上升段狀態曲線Fig.5 Flight curve for norminal ascent trajectory

圖6 推力損失下發動機單獨控制配平結果Fig.6 Trim results of engine control for loss of thrust

由圖6可以看出，在單臺發動機推力損失比例Rp在60%以下時，不同故障時刻均能夠實現配平。隨著推力損失比例的增加，擺動發動機產生的控制力矩減小程度增大，由推力損失引起的不對稱力矩也逐漸增大，若推力損失60%以上時，會出現不可配平情況，且不可配平情況與故障發生時間有關，故障發生在約50～80 s之間時，配平能力下降最為嚴重。由圖5可知該時間段為最大動壓飛行段，機體氣動力矩隨動壓增加，故推力損失故障下配平能力下降較為明顯，而低動壓區推力損失對配平能力的影響則不太顯著。單臺發動機故障關機是單臺發動機推力損失的特例，即推力損失比例為100%的情況。由圖6可以看出，單臺發動機故障關機下所有故障時刻均不能配平，這主要是因為單臺發動機關機情況下只剩2個控制量，無法控制3個通道飛行，故不能配平。

由圖6(a)和圖6(b)比較看出，故障發動機不同，其配平能力也不相同。主要是由于不同發動機故障下，推力損失產生的不對稱力矩的方向與機體氣動力矩的方向相同或相反造成的。1#發動機推力損失會產生正的偏航不對稱力矩，相反2#發動機故障偏航不對稱力矩為負。而在60 s附近機體偏航氣動力矩基本為正。因此，2#發動機故障產生的不對稱力矩剛好可以抵消掉一部分機體偏航氣動力矩，而1#發動機產生的不對稱力矩則進一步增加了需要的控制力矩，故在圖6 中60 s附近2#發動機推力損失下配平能力明顯強于1#發動機故障情況。

單臺發動機推力損失故障下，配平能力不足時，需采用發動機/氣動舵復合控制方式，配平結果如圖7所示。可以看出，由于引入氣動舵面進行控制，控制冗余度增加，故障下配平能力較圖6明顯改善，大部分故障時刻均能夠實現配平。但在推力損失較大且故障發生在約90 s以后時，配平能力仍顯不足。究其原因，是由于90 s以后，飛行高度較高，動壓較低，氣動舵效有所降低，沒有足夠的能力產生期望的力矩。

圖7 推力損失下復合控制配平結果Fig.7 Trim results of combined control for loss of thrust

在復合控制也不能配平的情況下，必須采取相應的應急策略保證飛行的安全。一種解決方法是通過調節健康發動機的節流閥值來減小單側發動機故障引起的不對稱力矩，從而減小故障對控制系統的影響。分析表明，將健康發動機推力調小10%時，即可將圖7中不可配平狀態消除。

3) 發動機擺動噴管卡死情況

由圖8(a)可以看出，對于噴管擺角δ1卡死情況，任意卡死角度下都不能夠配平。這是由于2臺發動機水平布置情況下擺角δ1和δ2用于同時控制俯仰和滾轉通道，在δ1卡死某一角度時，剩余的一個控制量δ2無法保證同時滿足俯仰、滾轉2個通道的控制需求，必然會造成不同故障時刻均不能配平。

圖8 擺動噴管卡死發動機單獨控制配平結果Fig.8 Trim results of engine control for stuck nozzle

3.3 整個空域內配平能力分析

整個空域內配平能力分析是在給定的攻角α、馬赫數Ma及飛行高度H范圍內進行配平特性計算。定義所研究的飛行狀態范圍內能夠配平的所有點的集合為可配平區域，不能配平的所有點的集合為不可配平區域。

在SRLV上升段飛行時，為了引入配平特性對飛行包絡的影響，除了考慮一般的彎矩及動壓等飛行約束外，還需要滿足配平飛行約束。定義同時滿足這3類飛行約束的所有點的集合為可飛區域。由于在(α,Ma,H)三維空間內研究可飛區域，在數據可視化及確定約束邊界方面都不太直觀，應尋求新的方法來描述可飛區域。考慮到每一組(Ma,H)都可計算得到對應的動壓q，因此可飛區域還可描述為滿足約束

(20)

的所有q-α空間內點的集合。這有利于確定考慮配平特性后的飛行約束邊界及可視化的實現，具體方法在后面算例中有所體現。

1) 正常飛行情況

采用前面提出的方法，對無故障情況下上升段配平特性進行計算，分析配平特性對飛行約束的影響。結合現有上升段氣動數據，選定在α∈[-10°,10°]、Ma∈[0.2,6]、H∈[0 km,60 km]范圍內進行配平特性計算。

計算結果如圖9所示。無故障下可配平區域占整個研究空域的84.76%。可以看出，若飛行高度H在約20 km以上時，可以實現配平，攻角和馬赫數對配平能力影響不大。這是由于飛行高度較高時，大氣密度快速衰減，使得飛行動壓及氣動力矩減小，因此配平能力較強。若飛行高度在約20 km以下，則大氣密度較大，在亞聲速段，氣動力矩才不至于太大，因此可以配平；馬赫數大于1時，不可配平區域與馬赫數和攻角的大小均有關。

圖9 無故障下三維不可配平區域Fig.9 3D nontrimmable region for norminal case

正常情況下上升段動壓約束為q≤30 kPa，彎矩約束|qα|≤1 300 N/m2·rad，則結合配平分析結果可給出考慮配平能力約束后的可飛區域如圖10所示。可以看出，無故障情況下只要滿足動壓和彎矩約束就能滿足配平要求，配平性能對可飛區域沒有影響，因此在軌跡設計或重構時不需要施加額外的配平能力約束。

2) 單臺發動機推力損失情況

單臺發動機推力損失故障對飛行約束的影響如圖11及圖12所示。1#發動機故障下，正攻角區域配平能力較差，結果表明推力損失程度在50%以下時，配平特性對動壓、彎矩約束不會造成影響。2#發動機故障下，負攻角區域配平能力較差，結果表明推力損失程度在50%以下時，配平特性對動壓、彎矩約束不會造成影響。

圖10 無故障下配平能力對可飛區域的影響 Fig.10 Trim capacity effects on flyable region for norminal case

圖11 1#發動機推力損失對飛行約束的影響Fig.11 Effects of loss of thrust of 1# engine on flight constraint

圖12 2#發動機推力損失對飛行約束的影響Fig.12 Effects of loss of thrust of 2# engine on flight constraint

對于推力損失嚴重的情況，由于配平能力下降嚴重，導致可飛區域減小，除了動壓約束和彎矩約束外，需要飛行中滿足配平約束條件。如圖11(b)、圖12(b)所示，為了簡化問題，配平能力約束邊界建模采用直線形式，由q-α空間A、B點位置坐標(αA,qA)、(αB,qB)可將配平能力約束表示為

(21)

代入具體數據可得1#發動機推力損失70%時配平能力約束為

q≤-96 592α+28 446

(22)

2#發動機推力損失70%時配平能力約束為

q≤116 870α+21 000

(23)

3) 發動機擺動噴管卡死情況

擺角δ1卡死-10°故障下配平分析結果如圖13 所示，若采用發動機單獨控制則整個空域內都不能夠配平，具體原因與與故障發生時刻配平分析相同。而采用復合控制后，故障對飛行約束的影響主要集中在氣動舵效較低的低動壓區，配平能力約束可近似表示為

q≥16 000 Pa

(24)

圖13 擺角δ1卡死-10°對飛行約束的影響Fig.13 Effects of δ1 stuck at -10° on flight constraint

4 結 論

1) 提出一種基于頂點投影法的相容性判定方法用于快速判定線性等式/不等式方程組解的存在性，并通過算例驗證了方法的準確性與計算效率。該方法對于任意線性等式/不等式混合方程組具有普適性，程序實現簡單，計算效率高。

2) 通過故障發生時刻配平能力分析，給出了亞軌道飛行器上升段發動機推力損失、擺動噴管卡死等故障模式下的不可配平區域，可為任務中止決策提供參考。同時就配平能力不足時的應急策略問題進行了探討。

3) 通過整個空域內配平能力分析，給出了不同故障模式下，考慮配平能力約束下的可飛區域，并建立了簡化的配平能力飛行約束數學模型，為后續故障后任務規劃、軌跡重構及制導等研究工作提供依據。

4) 本文提出的方法也適用于無動力飛行段氣動舵面故障情況下配平能力分析。

[1] GONZALEZ P. Influence of the abort capability in reusable systems reliabilit-FESTIP results overview: AIAA-1999-4928[R]. Reston: AIAA, 1999.

[2] 李新國, 王文虎, 王晨曦. 亞軌道飛行器上升段故障模式分析與仿真[J]. 飛行力學, 2014, 32(3): 235-238.

LI X G, WANG W H, WANG C X. Failure mode analysis and simulation of ascent trajectory for suborbital reusable launch vehicle[J]. Flight Dynamics, 2014, 32(3): 235-238 (in Chinese).

[3] HANSON J M. A plan for advanced guidance and control technology for 2nd generation reusable launch vehicles: AIAA-2002-4557[R]. Reston: AIAA, 2002.

[4] 陳永剛. 亞軌道飛行器控制系統設計[D]. 西安: 西北工業大學, 2008: 14-15.

CHEN Y G. Control system design of the sub-orbital vehicle[D]. Xi’an: Northwestern Polytechnical University, 2008: 14-15 (in Chinese).

[5] JACKSON M C, HU H. Autonomous ascent abort planning applied to military and civilian space launch vehicles: AIAA-2004-6586[R]. Reston: AIAA, 2004.

[6] SHAFFER P J. Optimal trajectory reconfiguration and retargeting for the X-33 reusable launch vehicle[D]. Monterey, CA: Naval Postgraduate School, 2004: 21-25.

[7] FAHROO F, DOMAN D. A direct method for approach and landing trajectory reshaping with failure effect estimation: AIAA-2004-4772[R]. Reston: AIAA, 2004.

[8] SHAFFER P J, ROSS I M, OPPENHEIMER M W, et al. Optimal trajectory reconfiguration and retargeting for a reusable launch vehicle: AIAA-2005-6148[R]. Reston: AIAA， 2005.

[9] SHAFFER P J, ROSS I M, OPPENHEIMER M W, et al. Fault-tolerant optimal trajectory generation for reusable launch vehicles[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(6):1794-1802.

[10] 解永鋒. 亞軌道飛行器應急返回與軌道重構技術研究[D]. 西安: 西北工業大學, 2011: 135-158.

XIE Y F. Research on emergency return and trajectory reshaping of suborbital reusable launch vehicle[D]. Xi’an: Northwestern Polytechnical University, 2011: 135-158 (in Chinese).

[11] 王娟, 劉小雄, 孫遜, 等. 基于優化配平的機翼故障飛機飛行性能分析[J]. 計算機工程與應用, 2014, 50(23): 229-233.

WANG J, LIU X X, SUN X, et al. Flight performance analysis for aircraft with wing faults based on optimization of trimming[J]. Computer Engineering and Applications, 2014, 50(23)： 229-233 (in Chinese).

[12] PARADISE J A. Adaptable method of managing jets and aerosurfaces for aerospace vehicle control[J]. Journal of Guidance, Control and Dynamics, 1991, 14(1): 44-50.

[13] JOHANSEN T A, FOSSEN T I, BERGE S P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J]. IEEE Transactions on Control Systems Technology, 2004, 12(1): 211-216.

[14] 徐方暖. 亞軌道飛行器上升段虛擬樣機設計[D]. 西安: 西北工業大學, 2008: 24-35.

XU F N. Virtual prototype design of the ascent of suborbital launch vehicle[D]. Xi’an: Northwestern Polytechnical University, 2008: 24-35 (in Chinese).

[15] 譚政. 亞軌道可重復使用運載器控制律研究[D]. 西安: 西北工業大學, 2009: 13-22.

TAN Z. Research on flight control laws of suborbital reusable launch vehicle[D]. Xi’an: Northwestern Polytechnical University, 2009: 13-22 (in Chinese).

[16] 宋恩民, 黃文奇. 判斷具有多線性約束條件的凸空間是否為空的交邊算法[J]. 計算機學報, 1996, 19(9): 704-708.

SONG E M, HANG W Q. An intersecting-side algorithm to determine whether convex regions bounded by multiple constraints are empty[J]. Chinese Journal of Computers, 1996, 19(9): 704-708 (in Chinese).

[17] 任世軍, 洪炳熔, 梁慶姿. 判定線性不等式構成的凸集是否空集的位置算法[J]. 哈爾濱工業大學學報, 2000, 32(2): 121-124.

REN S J, HONG B R, LIANG Q Z. A point positioning algorithm to determine whether convex regions bounded by multiple linear constraints are empty[J]. Journal of Harbin Institute of Technology, 2000, 32(2): 121-124 (in Chinese).

[18] 任世軍. 判定線性不等式圍成的空間是否為空的梯度快速算法[J]. 哈爾濱工業大學學報, 2006, 38(9): 1441-1445.

REN S J. Fast projection algorithm to determine the emptiness of regions bounded by linear constraints[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1441-1445 (in Chinese).

Trimcapacityanalysisofsuborbitalreusablelaunchvehiclewithenginefailure

WANGWenhu*,HANBing

CollegeofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051,China

Inordertoanalyzethetrimcapacityofthesuborbitalreusablelaunchvehiclewithenginefailure,theproblemoftrimcapacityisconvertedtotheproblemofcompatibilitydecisionoflinearequality/inequalitymixtureequations.Amethodbasedonvertex-projectionisproposedandusedintrimcapacityanalysis.Theaccuracyandefficiencyofthemethodareverified.Intheframeworkoftrimcapacityanalysis,thetrimcapacitiesatfailure-timeandforstate-spaceunderdifferentfailuremodesareanalyzedrespectively.Moreover,contingencystrategyisgiveninthecasethattrimcapacityisinsufficient.Simulationresultsindicatethatthemethodcanrapidlycalculatenon-trimmableregion,andanalyzetheinfluenceoftrimcapacityonflyableregion.Theseresultshaveimportantreferencevaluesforabortstrategyandaborttrajectoryoptimization.

suborbitalreusablelaunchvehicle;enginefailure;trimcapacity;compatibilitydecision;mixedequations

2015-12-28；Revised2016-05-27；Accepted2016-08-22；Publishedonline2016-08-261042

2015-12-28；退修日期2016-05-27；錄用日期2016-08-22； < class="emphasis_bold">網絡出版時間

時間：2016-08-261042

www.cnki.net/kcms/detail/11.1929.V.20160826.1042.004.html

*

.Tel.：0351-3557452E-mailwwhu@nuc.edu.cn

王文虎， 韓冰． 亞軌道飛行器發動機故障下配平能力分析J． 航空學報,2016,37(12):3646-3656.WANGWH,HANB.TrimcapacityanalysisofsuborbitalreusablelaunchvehiclewithenginefailureJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3646-3656.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0240

V448.1

A

1000-6893(2016)12-3646-11

王文虎男， 博士， 講師。主要研究方向： 飛行器動力學與控制。Tel.: 0351-3557452E-mail: wwhu@nuc.edu.cn

韓冰男， 博士， 講師。主要研究方向： 飛行動力學建模與仿真。Tel.: 0351-3557452E-mail: chihb2008@live.cn

URL：www.cnki.net/kcms/detail/11.1929.V.20160826.1042.004.html

*Correspondingauthor.Tel.：0351-3557452E-mailwwhu@nuc.edu.cn