平均數的教學不能離開統計意義
任景業
【編者按】小學階段,為了適應學生思維發展的規律和認知規律,很多數學知識在呈現上會有“不嚴謹”或是“不規范”的現象,這需要教師在教學中有左右逢源的視域和上通下達的關照。然而,就有部分教師在處理這些概念時,采取“快意恩仇”的處理方式。短期看來,能夠保證學生解題的成功率,長遠看來卻不利于學生的可持續發展。這其實是教師專業知識缺失的一種典型表現,打鐵還需自身硬,教師自身專業知識的完備,才能使自己在開展教學活動時游刃有余,本期將結合具體課例圍繞“完善小學數學教師專業知識”展開討論。
這是一位教師發在新浪博客中的一篇博文(博主:秋葉書齋齋主)。
一個周六的下午,我正在趕一篇論文,兒子拿著一道題很迷惑地問我:“媽媽,這道題是怎么回事呀?”我一看——“如果你語文、數學、英語的平均成績是92分,語文91分,數學90分,英語多少分?”就沒好氣地說:“上課沒聽講,對吧?這么簡單的應用題都不會做。”兒子委屈地分辯:“我聽了!平均不就是同樣多的意思嗎?可是為什么我語文數學英語一定要考同樣多的分數?”我簡直忍俊不禁了,笑著說:“不是說要你考同樣多的分數,而是你考了不同的分數,算出三門功課的平均成績。”“為什么要算出我三門功課的平均數?”兒子進一步追問。我一聽這小子要打破砂鍋問到底了,趕緊隨便找了個理由把他哄開了,否則一個下午也和他說不清。可是沒過一會兒,他又來了:“媽媽,這個又是怎么回事嘛?”再一看,還是類似的題:“今年小明9歲,爸爸39歲,媽媽36歲,小明一家今年的平均年齡多大?”我有點不耐煩了:“你今天怎么回事?老算不出這么簡單的數學題!”兒子一聽,大聲嚷嚷起來了:“我會算!可是為什么要算一家人的平均年齡呢?爸爸、媽媽、兒子的年齡怎么可能一樣大呢?”我抬頭看見兒子因“憤怒”而漲紅了的小臉,忽然語塞。是呀,明明三門功課成績不一樣,為什么要假設它們一樣呢?計算一家三口兩代人的年齡平均值就更是純粹的數學數字游戲,算出來有什么意義呢?可這在小孩看來,無法理解、毫無意義的數字游戲,偏偏在成人的世界中最為盛行——人均收入、人均居住面積、人均綠化面積等等。而這些平均數又意味著什么呢?
從這一段描述我們至少可以看出兩個問題:第一,孩子知道平均數怎么算,但不知道為什么要這么算。第二,教師編撰的習題僅停留于平均數的算法意義,而沒有體現出平均數的統計意義。由此,學生也就不能理解學習平均數的真正意義。
現象體現本質,教師對于“平均數”認識的缺失應是主因。回過頭來看,平均數首先是一個統計量,它的意義是為了說明一組數據的統計特征。
一、怎樣理解平均數的意義
理解平均數可以從以下三個方面去理解:
1. 怎么算平均數,也就是計算平均數的程序,即用被平均的數加起來除以數值的個數或通過均分幾個量求得平均數。說簡單一些就是“先加再除”,這是算法程序方面的理解。2. 在什么情境中用平均數。不僅僅知道怎么算,還要知道在什么情境下怎么正確地運用它解決生活中的問題,能求在不同情境下的平均數。這是第二方面的理解。3. 平均數是代表和理解一組數據的一個代表值,是描述和比較數據的統計量。
以前在教學“平均數”的概念時,教師往往把教學重點放在平均數的字面含義和求法上,而對平均數在統計學上的意義和作用很少提及。也就是關注的是第一條,而弱化的是最重要的一條——平均數的統計意義。
這里要注意,平均數是“描述和比較數據的統計量”。這涉及兩個方面的“描述”和“比較”。在統計活動中,平均數有時作為一組數據的代表,獨立描述這組數據的集中程度,如下文的“看一看每次可以記住幾個數字”與“競賽成績統計表”等。有時又與其他組的數據進行比較。就如——
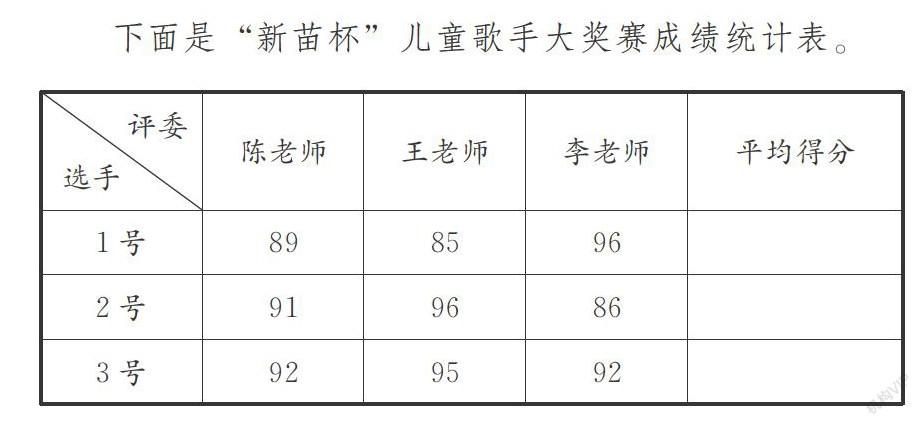
下面是“新苗杯”兒童歌手大獎賽成績統計表。
(1)你是怎樣理解平均得分的?與同伴交流你的想法。
(2)請你把這張成績統計表填寫完整。
(3)請你排出三位選手的名次,并與同伴交流你的方法。
在這個題目中,不同的評委對同一個選手的評分是不一樣的。選擇誰的評分作為選手的成績?在這樣需要兩組數據總體水平的比較中,平均數就應當上場了。這樣的情境比前面博文中孩子做的題目更接近平均數的統計意義。
二、教學建議
1. 在教學中要突出平均數的統計意義。
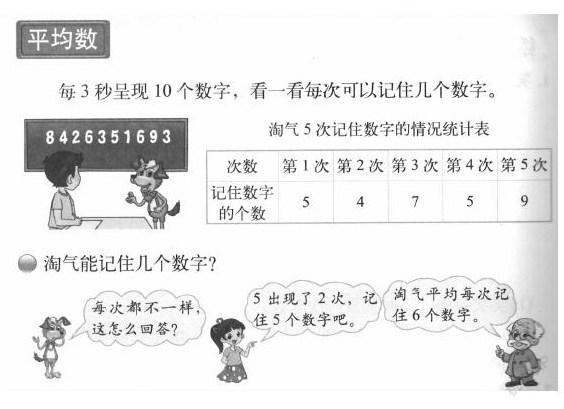
在北師大版教材中,四下“平均數”一課設計了一個記憶數字的游戲:“每三秒呈現10個數字,看一看每次可以記住幾個數字。”在這個游戲中,要讓學生理解“看一看每次可以記住幾個數字”的意思,它不是一次能記住幾個數字,是做過多次后,得到一組數據,然后選擇一個能代表這組數據的代表值。其實,這可以看成是測試一個人記憶能力的小測驗。結合淘氣5次記住數字的統計表,取其中任何一個數據都不能代表淘氣的記憶能力(當然,用最大值也未嘗不可,關鍵看如何制定標準),這需要一個代表值,由此讓學生體會平均數的統計意義。
數學中,不建議給出平均數的計算公式。這樣更有利于學生理解平均數的意義。
蔡金法博士的研究發現,亞洲和美國在教學平均數的內容時,有明顯的不同。亞洲系列更多的是對算術平均數這一算法的概念性和操作性理解,而不僅僅是把它看成一組數據的代表;美國的教材更多的是從一種統計學的角度而不是算法的角度來理解這個概念。美國教師強調學生應把平均數作為數據的代表來理解,而不是給學生演示算術平均數的算法。在美國的“教師用書”上很明確地指出五年級的學生沒有必要學會平均數的計算方法,只是會估計就行了,如估計一個月的平均氣溫。在學生形成平均數的統計學意義的直覺后,才要求他們解決該教材中的例子。因為各國國情不同,我們不能說美國五年級的學生沒有必要學會平均數的計算方法,只是會估計就行了,這個要求是不是太低,但他們并不過早地提供學生算法,而是讓學生更多地從一種統計學的角度而不是算法的角度來理解平均數的概念,對我們是很有啟發的。
2. 在實際應用中理解統計意義。
我們看下面的一個例子。
哪個班的成績好些?
數學是國際通用的科學語言,“作為語言課,首要任務是會使用它來表達思想”。(張奠宙等《數學教育學》),平均數也是如此。本題中給出了兩個班的原始成績記錄,一個班的數據有23個,一個班的數據有20個,要比較這兩個班的成績需要找到一個能代表各班成績的代表值。由本題可以讓學生體會平均數的統計意義,而非是一個算術習題。
當然,這樣的問題是很多的。可以比一下不同班級學生的身高、體重等生理指標,也可以選取體育賽事中的某項目成績。總之,要讓學生在實際的應用中體會統計量的意義。
教學中要為學生盡可能多地提供足夠的實際背景的問題,讓學生思考,舉例、解釋、討論,分享他們的看法。如,哪個國家的人更長壽些?有資料說,圣馬力諾男性平均壽命為83歲,是不是這個國家的人到83歲就死亡呢?是不是在死亡的人中沒有低于83歲的人呢?哪家快遞公司到貨更快些?有個公司說:他們發貨平均3天到。如果你發的貨第四天沒到,你會找快遞小哥“理論”嗎?
3. 讓學生親自參與統計,體會統計量的意義。
先看一個資料:
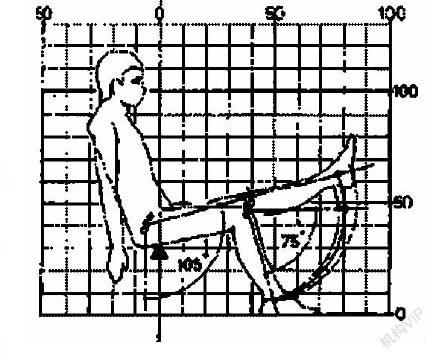
人類工程學是一門建立在工程學、醫學、心理學、解剖學、人類學、信息論等一系列科學基礎上的新興邊緣學科。人體尺寸是人類工程學最基本的數據,是產品設計中不可缺少的資料。左圖是從《人體動作尺寸圖集》[(日)小原二郎編,張福昌譯]中選取的一幅。請說出根據此圖設計合適的座椅時應注意的幾個數據。
現在的工業設計、企業規劃、國家決策常常會用到大數據。一提大數據似乎離小學生很遠,離我們的教學很遠。其實,大數據也是統計思想的應用。由此,我們可以讓學生自己測一下班里的同學的手長、腿長,身高、腳長,進行不同的活動時需要的空間,據此給出一些設計的建議。如,桌子應當多高合適?黑板多高才能適合四年級的學生書寫?板報的字寫多大才能看得清……這些問題的解決,需要用到眾多的數據,而這些數據的采集就是很好的統計活動。這些活動,又離不開平均數。因為設計的桌子、黑板、樓梯,不能只照顧特殊人群,需要選擇這些數據的代表值以代表這些數據的特征。
(作者單位:山東省茌平縣杜郎口中學)

