定積分計算的方法與技巧

劉春艷

(山西大同大學數學與計算機科學學院,山西大同 037009）

定積分計算的方法與技巧

劉春艷

(山西大同大學數學與計算機科學學院,山西大同 037009）

定積分的計算常用的方法有三種,本文從另外的5個方面對定積分計算的方法與技巧進行了探究,因而拓寬了解題思路,提高了解題效率。

定積分;計算;方法

定積分的計算,一般情況下采用牛頓—萊布尼茲公式、換元法、分部積分法等方法,但有些定積分的計算是需要一些特殊的方法與技巧,這樣可以大大的減少計算量,提高計算效率[1-6]。下面就一些方法與技巧進行探討。

1 利用定積分的幾何意義進行求解

例1求圓(x-a)2+y2=R2(0＜R＜a)繞y軸旋轉一周后的旋轉體體積。

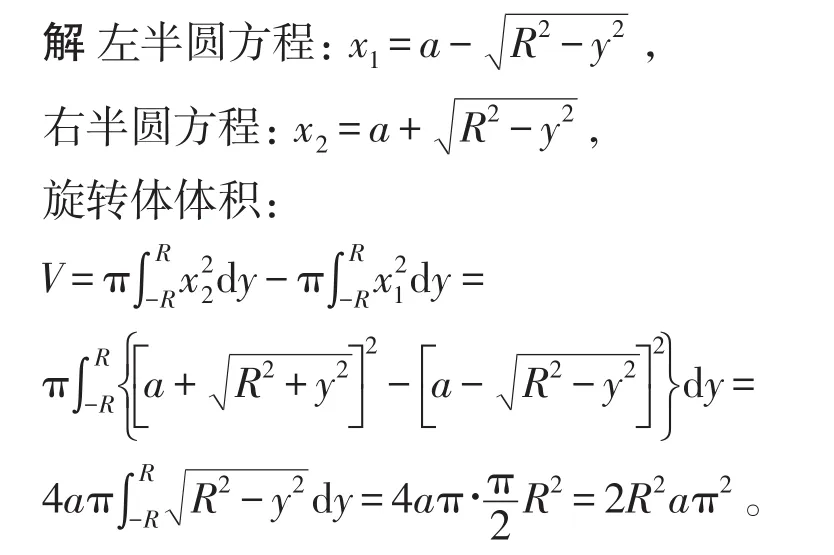
2 利用對稱性進行求解

在定積分的計算中,若積分區間關于原點對稱且被積函數具有奇偶性,則可以簡化積分運算。而當定積分不滿足這兩個條件時,可采用以下方法進行轉化：若積分區間不關于原點對稱時,可通過換元法變成關于原點對稱區間,若被積函數f(x)的定義域關于原點對稱且是非奇非偶函數時,則f(x)可以寫成一個奇函數和一個偶函數,即：

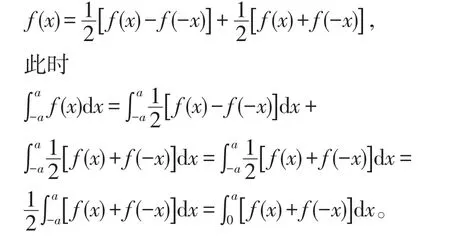
此積分比f(x)的積分簡單,就達到目的。

分析：在計算這個積分時,由于被積函數含有根式,往往會采用三角代換或雙曲代換來去掉根號,但這種方法計算量大,下面我們采用定積分的對稱性和幾何意義來計算

3 利用建立方程或方程組進行求解

在計算某些定積分時,有時需要通過換元積分和分部積分等列成一個方程或方程組進行計算。

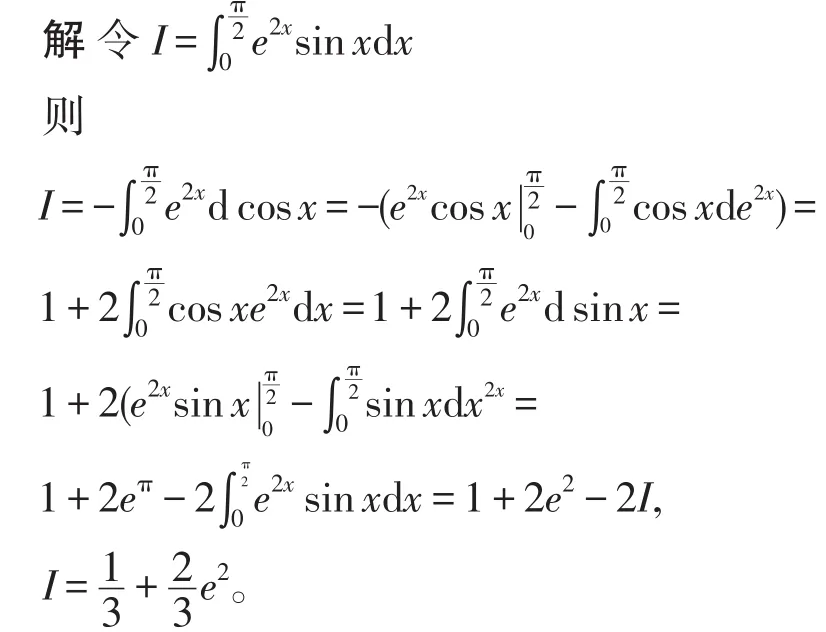
4 利用二重積分進行定積分求解

在計算二重積分一般是將二重積分化成二次積分計算,現在利用逆向思維將定積分轉化二重積分的計算。

5 利用含參變量進行定積分求解

在計算定積分時,有時可以在被積函數中引入參變量,通過含參變量的性質來求定積分。

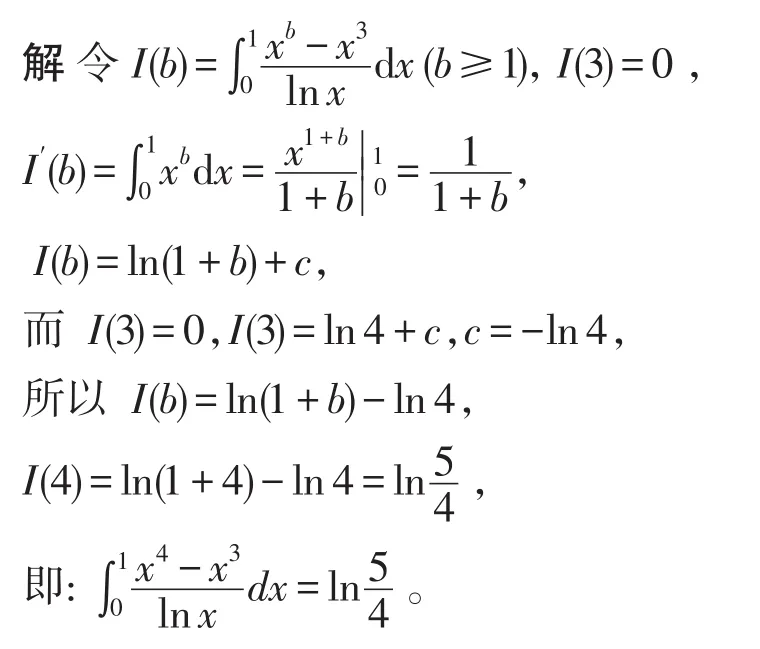
[1]周建瑩,李正元.高等數學解題指南[M].北京：北京大學出版社,2002：239-240.

[2]孫濤.數學分析經典習題解析[M].北京：高等教育出版社,2004：262-264.

[3]舒陽春.高等數學中若干問題解析[M].北京：科學出版社,2005：101-102.

[4]寧榮健.定積分計算的方法和技巧[J].工程數學,1995(1)：199-203.

[5]楊羅輝.關于定積分計算中的技巧性[J].長春大學學報,2005(4)：55-58.

[6]劉永莉,宋學梅.巧解定積分計算問題的幾種方法[J].數學教育研究,2009(10)：50-52.

〔責任編輯 高海〕

Methods and Techniques for Computation of Definite Integral

LIU Chun-yan
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi,037009)

There are three common methods for computation of definite integral.The thesis broadens the thinking of solving problems and improves the efficiency of solving problems by studying other five methods.

definite integral;calculation;technique

O175.5

A

1674-0874(2016)03-0008-02

2015-10-09

劉春艷(1965-),女,山西大同人,副教授,研究方向：高等數學。