大數據背景下高校貧困生類別的判定
——以安徽師范大學為例

齊懷峰

(安徽師范大學 學生工作處，安徽 蕪湖 241000)

?

大數據背景下高校貧困生類別的判定
——以安徽師范大學為例

齊懷峰

(安徽師范大學 學生工作處，安徽 蕪湖 241000)

目前高校貧困生的精準認定是一個公開的難題。本文以某高校連續60天的校園卡消費記錄為依據，利用Python語言和K-Means聚類算法，依據15545名大學生個人消費金額，而將他們分5個“最優群體”。從最低消費群體中挖掘應該被認定為貧困生而沒有被認定為貧困生的群體，從最高消費群體中挖掘不應該被認定為貧困生而被認定為貧困生的群體。本文以客觀的消費記錄為標準，利用大數據挖掘技術，為科學資助和精準資助提供了決策支持。關鍵詞： 大學生；貧困生；K-Means；分類；判定

目前高校貧困生的精準認定是一個公開的難題,其認定難點主要在于界定標準的確定和認定成本方面(學校無法走訪每一位大學生的家庭情況、貧困生個人情況也無法公示接受師生監督，只能依靠認定者的觀察和判定，以致于主觀因素影響較大)，再加上假貧困生爭奪濟困資源的行為客觀上又加大了認定難度。本文以某高校連續60天校園卡消費記錄(2016年2月22日-4月21日，共8616889條消費記錄)為依據，采用K-Means聚類算法，將15545名(大一至大三本科生，其中貧困生4189人，占總人數的26.95%)大學生個人消費總金額分5個“最優群體”(群體內消費相似而群體間差異較大)。從最低消費群體中挖掘應該被認定為貧困生而沒有被認定為貧困生的群體，從最高消費群體中挖掘不應該被認定為貧困生而被認定為貧困生的群體。本文以客觀的消費記錄為標準，利用大數據挖掘技術，為科學資助和精準資助提供了決策支持。

一、 數據處理及一般性統計分析

(一) 三餐消費的定義

為保持數據的連貫性，早餐時段定義為：00:00：00 - 09:59:59；午餐時段定義為：10:00:00-15:59:59；晚餐時段定義為：16:00:00-23:59:59。凡是在此三個時間段內發生的消費(含用校園卡購買其它物品，也就是說是廣義的三餐消費)，均被統計為早中晚三餐的消費金額；每位學生在某一時段可能消費多次，但都合并為某一餐的消費總金額。

(二)單次異常消費數據的處理

不失一般性，結合目前的消費水平，將三餐消費上限定義為：早餐15元、午餐25元、晚餐25元。若某單次消費超過限定額度，則被視為異常消費，并按消費上限記錄為此次消費金額(例如：若某一次晚餐消費100元，則按25元的上限記錄為此次消費金額)。

(三)缺失消費數據的處理

理論上，三餐消費總次數應該為2798100次(15545人*3次/人*60天)，然而并不是每個大學生在60天中，每天都在食堂消費3次，實際上其缺失數據相當多(詳見圖表2-4)。本文對缺失數據采用兩種處理方法：第一種是忽略缺失數據(如果某日某餐未用校園卡消費，則記錄為0元)；第二種是如果某日某餐未用校園卡消費，則此次消費被統計為該類型消費平均值(早餐：3.89元；午餐：8.18元；晚餐7.26元)。

(四) 消費群體的基本分析

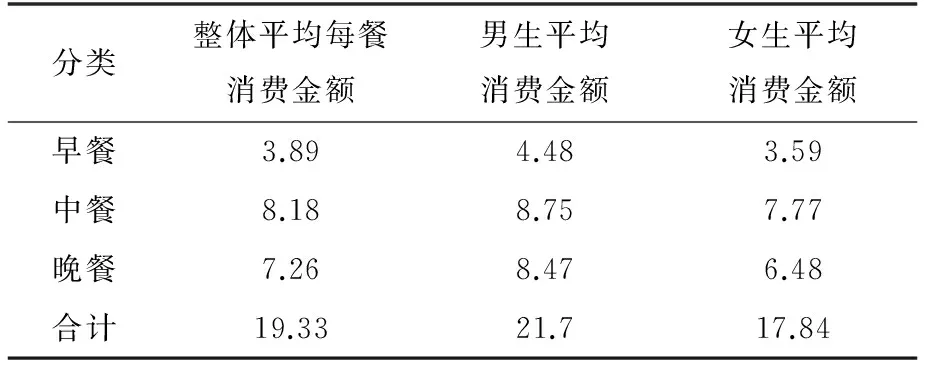
表1 性別餐飲情況統計表

表1顯示：男生的三餐金額均超過女生，平均每天消費超過女生3.86元，這與實際情況基本吻合。 表2顯示：目前大學生早餐就餐率尚不足50%，這是一個很嚴重的問題(午餐、晚餐可以選擇校外就餐，而早餐一般只在校內就餐或不吃)，需要加大此方面的宣傳教育，并采取相應措施；中餐和午餐的就餐率也只有70%，這說明因為學校食堂提供的飯菜不合口味，而導致約30%的學生選擇外賣或校外就餐，因此食堂飯菜水平應考慮提升；從標準偏差來看，早餐2.39，晚餐也只有5.47，這說明學生在食堂消費金額比較穩定，也就是說食堂提供的飯菜數量和款式比較單一。

表2 整體餐飲情況統計表

表3 非貧困生餐飲情況統計表

表4 貧困生餐飲情況統計表

從表2-表4，可以看出非貧困生和貧困生的消費狀況是有差異的，具體比較見表5。

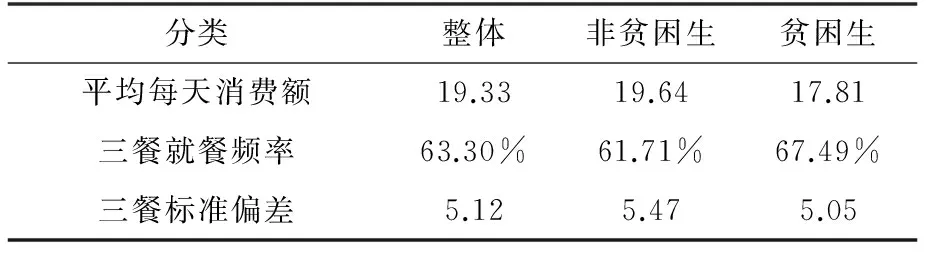
表5 非貧困生和貧困生消費數據比較

表5顯示：(1)非貧困生每天消費19.64元，而貧困生每天消費17.81元，非貧困生確實比貧困生在消費上有明顯差別；(2)非貧困生在校內就餐頻率為61.71%，貧困生在校內就餐頻率為67.49%，這說明由于經濟條件的限制，貧困生更多選擇在便宜的校內就餐；(3)非貧困生的標準偏差是5.47，貧困生的消費偏差是5.05，這說明貧困生的消費種類和價格的變化程度比非貧困生小或者說可選擇消費的余地比較小。

二、 基于K-Means聚類算法的群體分組

對15545條消費記錄(每人60天的消費記錄之和為一條記錄)的分類標準是一個需要研究的問題。本文采用無監督學習的K-Means聚類算法，將消費記錄分為5組，以便研究最低和最高的消費群體的消費情況。群體分組的標準采用輪廓系數(Silhouette Coefficient，是聚類效果好壞的一種評價方式。它結合內聚度和分離度兩種因素，可以用來在相同原始數據的基礎上用來評價聚合效果，取值范圍是(0,1))進行評價，該值越高則說明分組效果越好，即群體內部數據越接近而群體之間數據差異越大。

在實際的聚類中，當分為3類時，SC最大為0.57，從聚類算法理論上說是最佳分類，但在實際應用中并不是最佳選擇。但為了研究兩極群體，本文選擇5個分類，以便研究兩極群體。因為貧困生占總人數的26.95%，因此若消費最少的A類群體人數比例小于26.95%，理論上都應該被認定為貧困生。但實際情況并非如此，詳見表6-7。

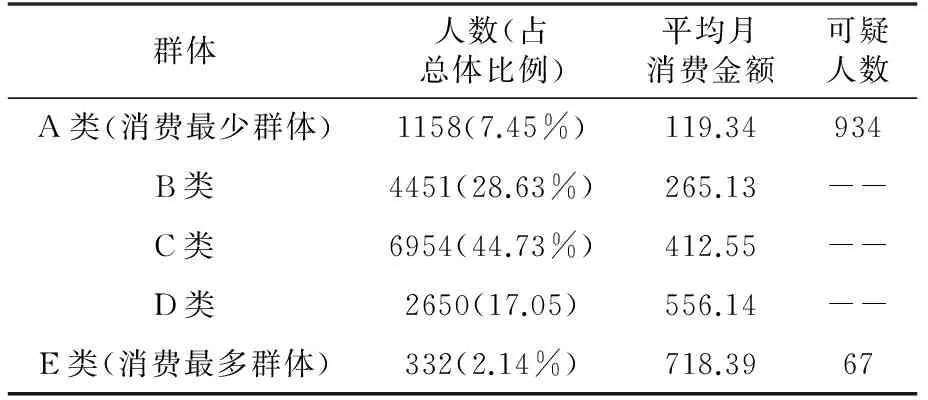
表6 未補充缺失數據消費統計表(SC=0.54)

表6顯示：因此A類(消費最少群體)有1158人應該被認定為貧困生，但聚類結果顯示，其中有934人不在貧困生庫中；E類(消費最多群體)有332人，但聚類結果顯示，其中有67人在貧困生數據庫中。

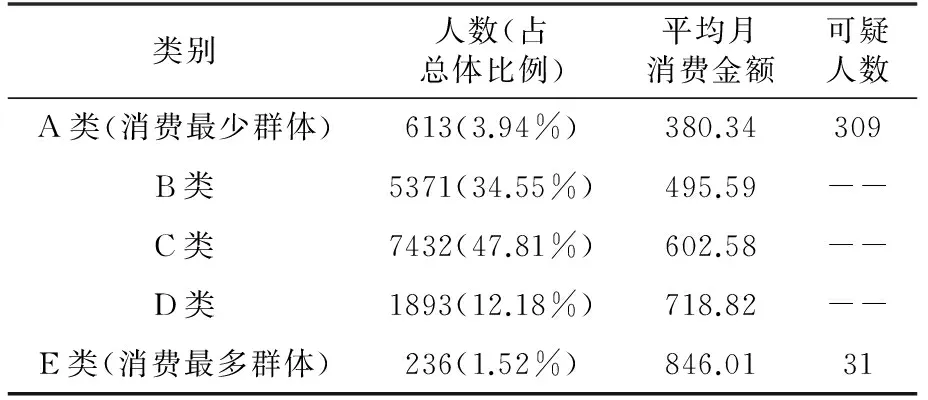
表7 已補充缺失數據消費統計表(SC=0.51)

表7顯示：A類(消費最少群體)有613人，但聚類結果顯示，其中有309人不在貧困生庫中；E類(消費最多群體)有236人，但聚類結果顯示，其中有31人在貧困生數據庫中。

三、 數據挖掘結果分析

表8顯示“未補充缺失數據”方法和“已補充缺失數據”方法中：A類相同人數有241人(交集)、最大可疑人數1002人(并集)；E類相同人數有25人(交集)、最大可疑人數73人(并集)。在A類消費群體中，雖然消費金額較低，但并不意味著他的真實消費額就低(學生消費是多元化的，比如外賣、校外就餐等)；在E類消費群體中，消費金額是最高的，若沒有特殊情況，一般不應再認定為貧困生。

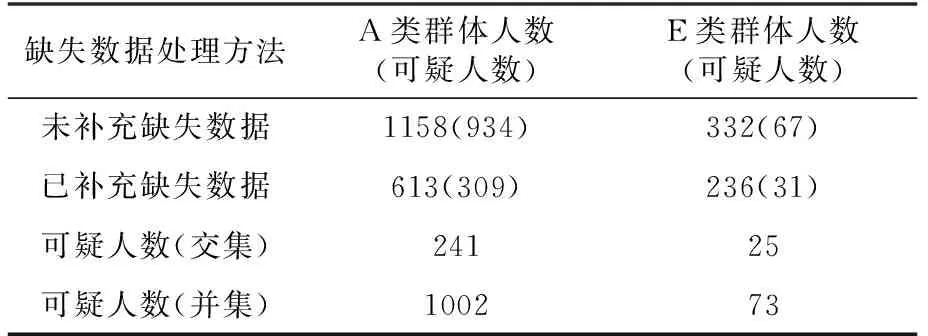
表8 兩種缺失數據處理方法的對比分析

在此基礎上，還可繼續做以下兩個方面的工作：一是對可疑的“貧困生”或“非貧困生”依據其60天的消費記錄和平時的消費表現進行觀察和分析，以便確定是其真正貧困或是其非貧困，實事求是的判定某一名大學生的貧困情況；二是在第一步的基礎上，判定采用哪種缺失數據處理方法(或二者結合)更為接近客觀事實，以便更有效的應用在實際工作中。

采用對消費記錄挖掘的方法，大大縮小了調查范圍、維護了貧困生的“忌貧心理”，能有效挖掘出“雖然貧困但不愿意申請”或“不貧困但申請貧困”的群體，節約了大量的人力資源成本。此外，利用大數據技術還可以為貧困生精準分類、“學霸”和“消費習慣”關聯等方面提供數據支持。

[1] Mastering Machine Learning with scikit-learn[M].UK:Packt Publishing,2014

[2] Python Data Visualization Cookbook[M].UK:Packt Publishing,2013

[3] 司維.Python基礎教程(第二版)[M].北京:人民郵電出版社，2014

[4] 楊知玲.數據挖掘在高校貧困生評價中的應用[J].軟件導刊,2016,(6)

[5] 吳文輝.高校經濟困難學生識別認定研究[J].辦公自動化,2016,(17)

[6] 畢鶴霞.大數據下高校貧困生確認模型構建——基于“模糊綜合評判法”與“模糊層次分析法”集成的實證研究[J].高教探索,2016,(8)

(責任編輯：樂程 )

How to Identify the Needy College Students against the Background of Big Data

Qi Huaifeng

(StudentAffairsDepartment,AnhuiNormalUniversity,Wuhu,Anhui, 241000,China)

This article bases itself on the campus card consumption of 15545 students from a certain university for 35 consecutive days. It uses Python language and K-Means clustering algorithm to categorize these students into 5 optimal groups according to the total amount of their personal consumption, picking out the ones from the group that consumed least who should have been identified as needy and the ones from the group that consumed most who should not have been identified as needy. The paper attempts to provide some decision support for financially aiding students in a scientific and precise way.

college student; needy student; K-Means; classification; identification

齊懷峰(1979-)，男，安徽師范大學學生工作處講師。

10.13585/j.cnki.gxfdyxk.2016.05.017

G641

A

1674-5337(2016)05-0074-04