函數中含參數零點問題的求解策略

寧夏彭陽縣第三中學 (756500)

杏望春

?

函數中含參數零點問題的求解策略

寧夏彭陽縣第三中學 (756500)

杏望春

函數零點是函數單元中的重要內容，它常常與方程、不等式等知識交匯，涉及到的題型大多是求參數取值范圍問題，給同學們的學習帶來一定的困難.為此，我們結合具體實例給出與零點相關問題的以下幾種常見的求解策略，以期對同學們的學習有所幫助.

1.把函數零點問題轉化為方程根的問題

利用函數y=f(x)的零點?方程f(x)=0的根.把求函數零點的相關問題轉化為求方程根的問題，通過方程的根所滿足的條件建立不等式來解決問題.

例1 若二次函數f(x)=x2-2ax+4在區間(1,+∞)內有兩個零點，求實數a的取值范圍.

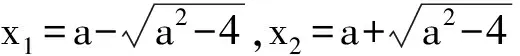
評析：若函數對應的方程的根易求得，我們可以通過解方程求出根，然后根據方程根所滿足的條件建立不等式組，從而求出參數的取值范圍，是解決這類問題的常用方法.

2.把函數零點問題轉化為函數圖像與坐標軸的交點問題

利用函數y=f(x)的零點?函數y=f(x)的圖像與x軸交點.把函數零點的相關問題轉化為圖像與坐標軸的交點問題，再利用數形結合的思想方法來解決問題.

解：f′(x)=x2+(1-a)x-a=(x-a)(x+1),由f′(x)=0得x=a，x=-1.列表

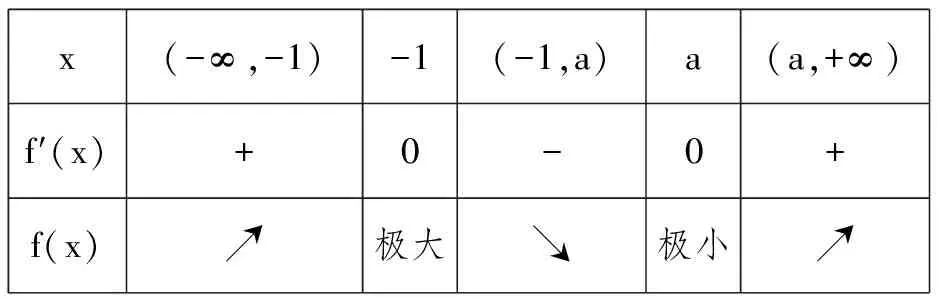
x(-∞，-1)-1(-1，a)a(a，+∞)f′(x)+0-0+f(x)↗極大↘極小↗

圖1

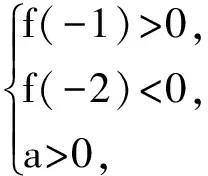
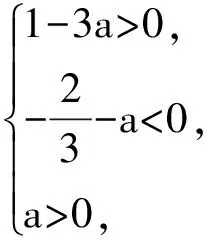
評析：利用函數的簡單性質做出函數的圖像，借助于圖像分析零點在所給定區間上時，圖像所滿足的條件建立不等式組求解.通過數形結合的方法輕松解決.

3.把零點問題分離變量后轉化為函數值域問題

將函數零點問題先轉化為方程根的問題,然后進行……