二元函數(shù)最值問(wèn)題的常用策略

浙江省寧波市第二中學(xué) (315010)

孫 鋆

?

二元函數(shù)最值問(wèn)題的常用策略

浙江省寧波市第二中學(xué) (315010)

孫 鋆

形如z=f(x,y)含有兩個(gè)自變量的函數(shù)我們稱為二元函數(shù)，其最值問(wèn)題常常是高中函數(shù)問(wèn)題中的熱點(diǎn)和難點(diǎn)問(wèn)題,而這類方法有時(shí)常常根植于解析幾何、向量等諸多高中數(shù)學(xué)重要知識(shí)，同時(shí)考查轉(zhuǎn)化化歸、分類討論等數(shù)學(xué)思想.根據(jù)自變量x,y的關(guān)系二元函數(shù)主要可以分為兩種基本類型，其一是x,y之間沒(méi)有聯(lián)系，其二是x,y之間存在聯(lián)系，這種聯(lián)系常表現(xiàn)為方程或不等式(組)關(guān)系.求解二元函數(shù)最值核心思想是化二元函數(shù)為一元函數(shù)即將復(fù)雜陌生問(wèn)題化歸為簡(jiǎn)單熟悉的函數(shù)模型，當(dāng)然利用柯西不等式可以直接處理二元最值問(wèn)題.以下我們談?wù)勄蠼舛瘮?shù)最值問(wèn)題的常用策略和方法.

1.基本不等式法

例1 已知x,y>0且x+4y+xy=5，求x+4y的最小值

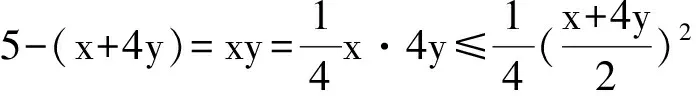
例2 若x,y>0且x+3y=5xy，求3x+4y的最小值.

評(píng)注:利用基本不等式求二元最值注意”一正二定三相等”,即不等式運(yùn)用的前提是正數(shù),構(gòu)造定值和取等號(hào)的條件.學(xué)生常常忽略等號(hào)成立的條件產(chǎn)生誤解(特別利用多次不等關(guān)系),此時(shí)往往需要轉(zhuǎn)為相關(guān)函數(shù)模型的單調(diào)性加以解決.同時(shí)更要善于尋找目標(biāo)和條件間的關(guān)系,熟悉湊配和1的代換等技巧.

2.消元法

事實(shí)上如上的例1和例2都可用消元法加以求解.不妨以例2加以說(shuō)明.

評(píng)注:用條件加以消元從而把二元函數(shù)一元化,在利用基本不等式或函數(shù)的單調(diào)性求最值,值得指出的是要關(guān)注函數(shù)的定義域,示例中即由x>0及y>0求出變量x的范圍,學(xué)生常常會(huì)忽略變量y對(duì)x的限制作用而導(dǎo)致定義域范圍擴(kuò)大.