一道2016摩爾多瓦數學奧林匹克試題別解及推廣

江蘇省姜堰中等專業學校 (225500)

陳 宇

?

一道2016摩爾多瓦數學奧林匹克試題別解及推廣

江蘇省姜堰中等專業學校 (225500)

陳 宇

2016摩爾多瓦數學奧林匹克試題

已知a,b,c是滿足a2+b2+c2+ab+bc+ca=6的正數，求a+b+c的最大值.

筆者在此給出兩個別解.

(法二)∵a,b,c是正數，由已知得6=a2+b2+c2+ab+bc+ca≥2(ab+bc+ca)?ab+bc+ca≤3,又a2+b2+c2+ab+bc+ca=6?(a+b+c)2=6+(ab+bc+ca)≤6+3=9?a+b+c≤3.

法一主要依據均值不等式適當放縮；法二則主要借助題設條件(也需依據均值不等式)適當變形再進行放縮，并求解.較之文[1]，此兩法思路更顯自然，無需技巧.

進而該賽題可推廣如下：

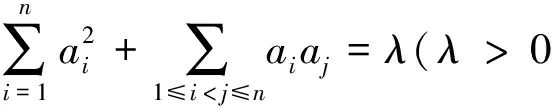
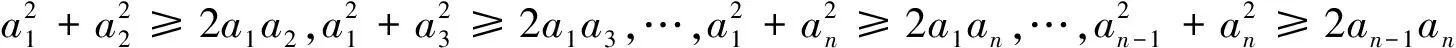
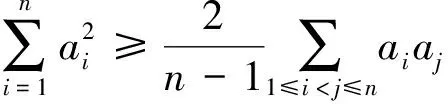
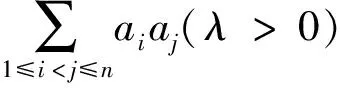
[1]周輝.2016年IMO不等式題的巧思妙解[J].中學數學研究(江西),2016,5(49～50).