例談解幾中向量應(yīng)用意識(shí)的培養(yǎng)

江蘇省金湖中學(xué) 秦利芳

例談解幾中向量應(yīng)用意識(shí)的培養(yǎng)

江蘇省金湖中學(xué) 秦利芳

向量知識(shí)作為工具，在數(shù)學(xué)、物理等學(xué)科的很多分支中有著廣泛的應(yīng)用。它具有代數(shù)形式和幾何形式的“雙重身份”，能融數(shù)形于一體，能與中學(xué)數(shù)學(xué)教學(xué)內(nèi)容的許多主干知識(shí)綜合，形成知識(shí)交匯點(diǎn)，是高考命題的熱點(diǎn)。但我國(guó)向量知識(shí)卻是在全面實(shí)施新課程后才作為教學(xué)內(nèi)容進(jìn)入高中數(shù)學(xué)教材的。學(xué)生還不太適應(yīng)用向量知識(shí)方法解題。在數(shù)學(xué)解題方面，向量應(yīng)用意識(shí)不強(qiáng)。如在解析幾何中有些問題總習(xí)慣用常規(guī)方法去解決，造成過程運(yùn)算比較繁雜，若能靈活運(yùn)用向量作形與數(shù)的轉(zhuǎn)化，則會(huì)大大簡(jiǎn)化過程。鑒于此，筆者想談?wù)勅绾闻囵B(yǎng)學(xué)生在解析幾何中應(yīng)用平面向量的意識(shí)。

一、在知識(shí)的構(gòu)建過程中，讓學(xué)生體會(huì)向量的工具性特點(diǎn)，感受向量方法的簡(jiǎn)潔性

【例1】利用向量知識(shí)來推導(dǎo)點(diǎn)到直線的距離公式。

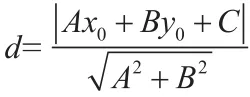
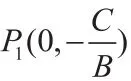
當(dāng)B=0時(shí)，可直接用圖形證明（略）。

評(píng)注：引導(dǎo)學(xué)生對(duì)比傳統(tǒng)證明方法，他們會(huì)發(fā)現(xiàn)向量法避免了復(fù)雜的構(gòu)圖過程，應(yīng)用向量來證，簡(jiǎn)單易懂，充分體現(xiàn)了向量的工具性和優(yōu)越性。所以筆者認(rèn)為先從學(xué)生熟悉的平面幾何問題入手，充分挖掘課本素材，在教學(xué)中從推導(dǎo)有關(guān)公式、定理，例題講解入手，讓學(xué)生去品位、去領(lǐng)悟，在公式、定理的探索、形成中逐漸體會(huì)向量的工具性，逐漸形成應(yīng)用向量的意識(shí)。

二、在平時(shí)的解題思維訓(xùn)練中，讓學(xué)生發(fā)現(xiàn)用向量法的思路清晰與運(yùn)算過程簡(jiǎn)潔的優(yōu)越性

【例2】已知定點(diǎn)A（-1，0）和B（1，0），P是圓（x-3）2+（y-4）2=4上的一動(dòng)點(diǎn)，求的最大值和最小值。……