巧用奇函數的性質解數學題

湖南省岳陽市第十五中學326班 李博亞

巧用奇函數的性質解數學題

湖南省岳陽市第十五中學326班 李博亞

函數是高中數學中的一個重要內容，也是難點之一。主要體現在函數思想的運用，而掌握函數的一個重要手段就是分析函數的性質。從函數的性質入手來求解數學問題，也是解決函數問題的非常適用的工具。而我們在解決函數問題時往往容易忽視的地方主要體現在：一是忽視從函數的本質特性入手，如定義域、對應法則、函數的單調性、奇偶性等。二是容易忽視分析題設所給式子的結構特征。因此，我們可以從奇函數的定義出發，證明出奇函數的性質，函數的性質是函數的靈魂。在解答一些類似很抽象的問題時，我們先從函數的性質入手，認識這個函數的本質特征，巧用其性質來解答，可以達到事半功倍的作用。

一、奇函數的定義及性質

在我們的教材中奇函數是這樣定義的：設函數y=f（x）的定義域為D,如果對D內的任意一個x,都有x∈D,且-f(x)=f(-x),則這個函數叫做奇函數。其中的關鍵詞有“D內的任意一個x”、“都有”“-f(x)=f(-x)”。用數形結合的思想來理解奇函數的定義就是：奇函數的定義域關于原點對稱，其圖形關于原點成中心對稱圖形。從這個定義出發，我們很容易證明奇函數具有如下四個性質：

性質1 對定義在區間D上是單調遞增奇函數f（x），如果a,b∈D，

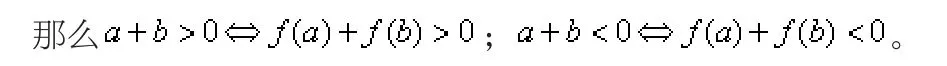
性質2 已知定義在區間D上的單調遞減奇函數f（x），如果a,b∈D，

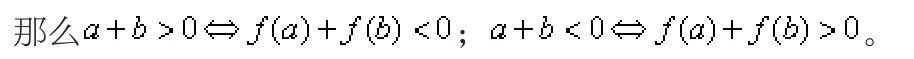
性質3 已知在區間D上的單調奇函數f（x），如果a,b∈D，

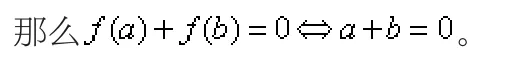
性質4 如果奇函數f（x）是定義在D上的奇函數，且有最大值M，那么f（x）的最小值為-M，反之亦然。……