蘇教版高中數學“基本不等式的證明”（1）教學設計

江蘇省淮安市第一中學 牛玉雷

蘇教版高中數學“基本不等式的證明”（1）教學設計

江蘇省淮安市第一中學 牛玉雷

教學目標：

一、知識與技能

1.經歷基本不等式的證明過程，感知證明不等式過程中運用的基本思想和方法；

2.運用基本不等式，初步學會解決簡單的最值問題；

3.學會探究并熟練掌握基本不等式，體會和深入理解基本不等式的幾何意義，并掌握定理中的不等號取等號的條件；

4.理解兩個正數的算術平均數不小于它們幾何平均數的證明過程，理解對它的幾何解釋；

二、過程與方法

1.借助實例，進而探究抽象出基本不等式；

2.引導學生借助數和形兩個方面，深入探究不等式的證明，進而進一步突破難點。

三、情感、態度與價值觀

1.通過新知探究，體會數學知識來源于生活，運用于生活的道理；

2.培養學生邏輯推理能力，并結合不等式的幾何解釋，拓展學生數形結合的豐富想象力。

四、教學重點與難點

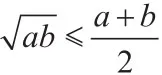
五、學法與教學用具：

1.學法：從引導學生觀察常見圖形入手，通過面積進行直觀比較，進而抽象出基本不等式。在定理證明的過程中，留給學生足夠的思考空間，引導他們自主探究。

2.教具：直角板、圓規、投影儀。

課型：新授課。

課時：1課時。

教學過程：

一、創設情境，引出新課

教師結合2002年8月在北京召開的第24界國際數學家大會的會標，引導學生發現圖案中一些相等關系或不等關系。

二、新課研討

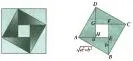
重要不等式的內涵：一般地，對于任意實數a、b，我們有a2+b2≥2ab，當且僅當a=b時，等號成立。……