Banach格上Dunford-pettis算子的AM緊性研究

西藏大學理學院 孫文濤

Banach格上Dunford-pettis算子的AM緊性研究

西藏大學理學院 孫文濤

在Banach格上研究Dunford-pettis算子的AM緊性，對Dunford-pettis算子為AM緊性的一些條件進行探究，在現有的基礎上已經得到了一些不錯的成果。

Banach格；Dunford-Pettis算子；AM-緊性

一、引言

設定E與F屬于Banach格，T：E→F屬于有界線性算子，如果T把E當中的弱收斂于零集映為F中的相對緊集，那么T叫做Dunford-Pettis算子；如果T將E中序區間映為F中的相對緊集，那么T屬于AM-緊算子；有關Dunford-Pettis算子和 AM-緊算子的性質和與其他特殊算子的聯系，已經有了很深的探究。本文主要討論了Banach格上Dunford-pettis算子的AM緊性研究。

二、Dunford-pettis算子的AM緊性

引理1.1 設定E屬于Archimedean Riesz空間而且。V在E中序稠只有當對于隨意u∈E＋，存在。當A輸運E的理想時，A在E中稠只有當E屬于A生成的帶。

引理1.2 設定E，F屬于Riesz空間并且F屬于Dedekind完備。D屬于Lb(e，f)的非空向上指標集。那么supD存在只有當隨意集合有上界，那么成立：。

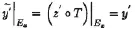
通過定理1.3 得知

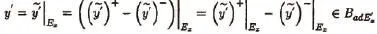
得證。

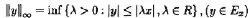
下列屬于AM-空間，它的閉單位球是[-|x|，|x|]。

以下是Dunford-Pettis算子屬于AM-緊算子的幾個充分條件。

定 理1.5 設 定E、F屬 于Banach格，T：E→F屬 于Dunford-Pettis算子，那么以下條件之一成立時T屬于AM-緊算子：（1）E擁有序連續范數；（2）對于隨意，Ex離散；（3）E'離散；（4）F屬于有限維空間。

證明：（1）E擁有序連續范數，那么E中任意區間都屬于弱緊的，T是Dunford-Pettis算子，把任意有界集映為相對范數緊集，所以T屬于AM-緊算子。

（2）T屬于AM-緊算子只有當任意是緊算子。以下證明對于每個屬于緊算子。事實上，對于屬于AL空間，因此Ex擁有序連續范數。但是Ex離散，因此可得屬于緊算子。

（4）由于T屬于緊算子，所以屬于AM-緊算子。

P.G.Dodds、D.H.Fremlin和J.Bourgain證明AL空間上的Dunford-Pettis算子構成一個帶。Aliprantis和……