數學課堂教學中的變異思想
山西長治市武鄉縣職業中學校 劉振江
數學課堂教學中的變異思想
山西長治市武鄉縣職業中學校 劉振江
課堂教學是整個教學過程的中心環節,也是學生獲取知識、發展智能的主要途徑。在課堂教學中,教師要通過各個環節,采用多變手段,激發學生情感,夯實基礎知識。
數學思想方法和基礎知識是數學大廈的支柱與橫梁。不難發現,教材中每一章、每一節直至每道例題、習題的解答,都是知識、思想和方法的有機結合,它們共同構建成數學教學中的基本內容,而且思想方法寓于基礎知識之中,以知識的發生和問題的解決為其形成展示的載體,在基礎知識的形成中,無不隱含著人們在數學活動中解決問題的途徑、方法和思想策略,無處不以數學思想方法作指南,數學思想方法不僅是知識技能通向提高能力素質的橋梁,也是推動數學發展的動力,可以說數學思想方法的教學是數學學科素質教育的核心,數學課堂教學必須著力注重于這一核心。
一提到高中數學,許多人就想到了題海戰術,并且對所謂的“模”、“函數”、“雙曲線”、“拋物線”視若畏途,但又不得不接近它。到底什么使我們的高中生對數學產生如此的心態呢?有人說“厭學”,那么又是什么是他們厭學呢?有人反駁說:“高中數學無味,并且內容又很抽象。學生聽起來很枯燥。這是學科特點決定的。”其實,這是給自己找借口,或者是根本沒有弄清數學的奧妙所致,是老師沒有發掘出其中的興趣所在。學生學,關鍵在于老師引。當然,要想引向成功,就要靠老師在課前的準備和課上的導學。
在高中數學的教學目的中,強調了進一步培養學生的思維能力、運算能力、空間想象能力、解決實際問題的能力,以及創新意識。可以說,學數學是培養能力,數學離不開數,離不開題,關鍵在于通過典型例題能把知識鞏固了,能形成技能,而且能夠遷移。
在課堂教學過程中,例題可以有的不講,有的可以加深講,有的可以解體。對同一個題,要通過不同角度去思考,這樣有助于思考問題的全面性和靈活性。能力的培養,創新意識的形成,要用專門的時間去研究,要融會在平常的學習中,在習慣中培養創新。
在教學過程中,要注重這些方面的培養,使學生能逐漸養成這種思考問題的習慣。
一、放風箏式教學法
因我教的班級是實驗班,學生的自學能力較強,所以我在課堂教學中經常使用此法。
例如,教學“含絕對值的不等解法”,就可以先放給學生自學,讓他們先自己閱讀課本內容15分鐘,接著讓兩位同學談談這一節的重點內容,老師總結這兩生回答的情況,并加以補充。然后,讓學生從課后各找兩個有代表性的題目,讓自己的同桌去做,然后互改。最后,老師補充兩個拔高題目:(1)已知|x-a|<b的解集是{x|-3<x<9},求a、b的值。(2)已知|x-1|<3,化簡|x-4|+|x+2|。這樣這一堂課就比較完美了,充分發揮了學生的自學能力和創造思維,經過課下了解,學生對這節課很滿意。
這種方法適用于教材內容不太難又不很抽象的,可以給自己的課堂教學增添一下特色。
二、解剖法
適合內容比較復雜而又不難的題目,并且能很容易看出怎樣做。

三、由淺入深法
這種思想一般老師經常用,但有時沒必要用,像比較容易的題目,而有些又不得不用,如果某些題目較抽象,我們可以逐步點撥學生去思考。在函數應用中有一道例題,如圖:有一塊半徑為R的半圓形鋼板,計劃剪裁成等腰梯形ABCD的形狀,它的下底AB是圓O的直徑,上底CD的端點在圓周上,寫出這個梯形的周長y和腰長x間的函數式。
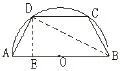
分析:先讓學生思考第一個問題,三角形ABD是什么三角形?第二個問題,若∠ADB=90°,證明AD2=AE×AB。這兩個問題解決了,也就等于為此題鋪好路了。
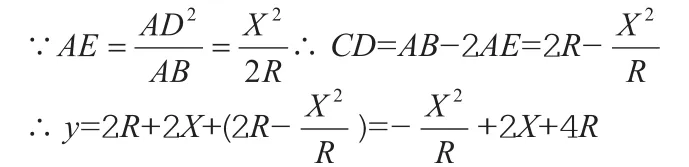
四、改頭換面法
此法是在做會此題的基礎上使用的,學生可以在自己做題的過程中加以聯想,充分調動思維,展開討論,若能達到這個水平,可以說解決問題已經上升到了一個高度。如:求圓心角,半徑r=45的弧長L。此題很容易,先把角度制轉化成弧度制,因為,所以。
五、移情法
如在學習完排列組合后,一些實際問題可以去用排列組合來解決,并且可以自己創造問題。例如:我們班57位同學,每人和其他人都握一次手(兩個人不重復,不漏握),試計算全體握手的次數。又如:我們班舉行一晚會,出兩人一男一女做主持人,只能從同一個組出,共有多少種可能的組合?(一組五男三女,二組四男四女,三組三男五女,四組四男四女,五組五男三女,六組五男三女,七組五男四女)這樣既增加了學習的興趣,又把所學的知識應用于實際,使同學們加深了對知識的理解和掌握,學生研究問題的能力就在實踐中慢慢培養出來了。
現在高中教材中所增設的研究性課題在數學方面主要是指對某些數學問題的深入探討,或者從數學角度對某些日常生活中和其他學科中出現的問題進行研究。這種變異思想很適合研究性課題的要求,并且充分地調動了學生的靈活性和創新思維,使他們的能力得到進一步提高。

