把握解題竅門，攻破數學難題

江蘇省大豐高級中學高三（16）班 王柏銘

把握解題竅門，攻破數學難題

江蘇省大豐高級中學高三（16）班 王柏銘

在數學解題中，有人歡喜有人愁，有人左思右想，絞盡腦汁，仍百思不得其解；有人轉換角度，另辟蹊徑，豁然開朗；有人乘勢而下，順水推舟，水到渠成。同一道數學題，有人思路明確，推理清晰，解法精妙獨到，簡單易懂；有人卻思維僵化，不知變通，解法呆板單一，繁瑣復雜。究其根源在于學生對解題“竅門”的把握。因此，在平時解題學習和復習過程中，同學們要注意把握解題竅門，攻破數學難題。

一、從數學概念和性質分析中探求解題竅門，破解數學難題

數學概念和性質是數學解題的重要基礎。在許多數學問題中，無論從題設條件、所求結論還是直觀圖象都或多或少地隱含著某種特征。在解題時，若能善于觀察，用心捕捉這些特征，聯想到與之相應的概念和性質，往往可以快速地找到解題的突破口，從而使問題迎刃而解。

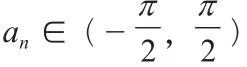
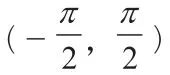
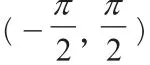
下面證明這樣的k是唯一存在的。

假設a1+a27=a2+a26=a3+a25=…=a13+a15=2a14＞0，由單調奇函數性質可知，

f（a1）+f（a27） ＞0，f（a2）+f（a26） ＞0，f（a3）+f（a25） ＞0，…，f（a13）+f（a15） ＞0，又因為f（a14） ＞0，所以f（a1）+f（a2）+f（a3）+…+f（a27） ＞0，這與題設條件相沖突。同時若a14＜0時，則有f（a1）+f（a2）+f（a3）+…+f（a27） ＜0，同樣也與題設條件相沖突。綜上所述，若則有f（a1）+f（a2）+f（a3）+…+f（a27）=0時，則當且僅當k=14時，f（ak）=0。

【評注】本題主要考查學生對函數奇偶性、單調性以及等差數列性質的綜合運用能力。在解本題時，只有把握了函數奇偶性、單調性以及等差數列性質這一解題“竅門”，才能使問題得以有效解答。

二、從特殊與一般的轉化中發現解題竅門，攻克數學難題

唯物辯證法告訴我們，事物之間是既有共性又有個性的關系。……