一類條件代數不等式的統一推廣

郭要紅 劉其右

（安徽師范大學數學計算機科學學院 241000）

2009年《數學通報》第8期數學問題1808如下：

問題1808[1]已知正數a，b滿足a+b=1，求證：

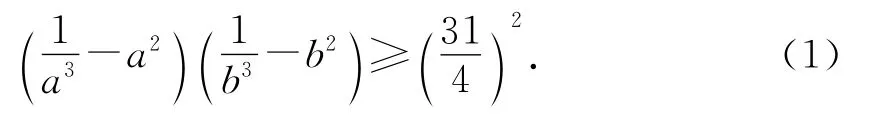
2010年《數學通報》第1期數學問題1833如下：

問題1833[2]已知a，b＞0，且a+b=1，求證：

對不等式（1）、（2），文[3]從項數與指數出發，給出了如下推廣：

定理1設，則

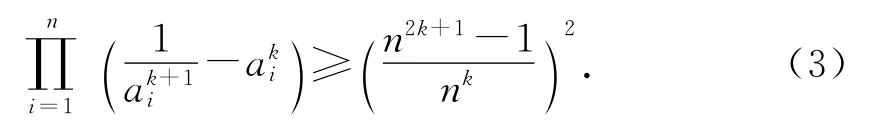
2015年《數學通報》第4期數學問題2238如下：

問題2238[4]已知x，y是滿足x+y=1的正實數，求證：

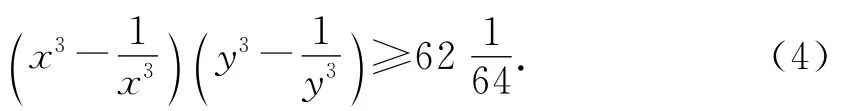
對不等式（1）、（2）、（4），文[5]從指數出發，給出了如下推廣：

定理2設a，b＞0，且a+b=1，對任意的正整數m，n＞2（m≥2），則有

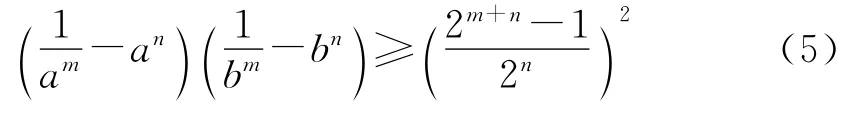
本文從指數與項數入手，給出不等式（3）、（5）的一個統一推廣.

定理3設n∈N*，p∈N*，q∈N*，ai＞0，則

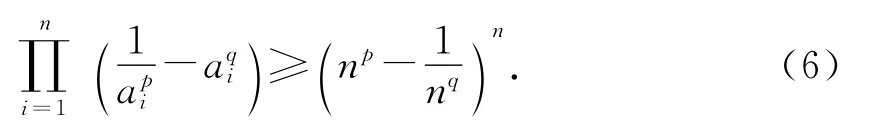
證明利用恒等式

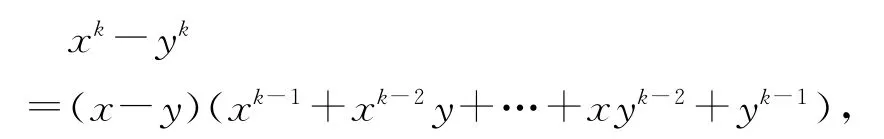
有

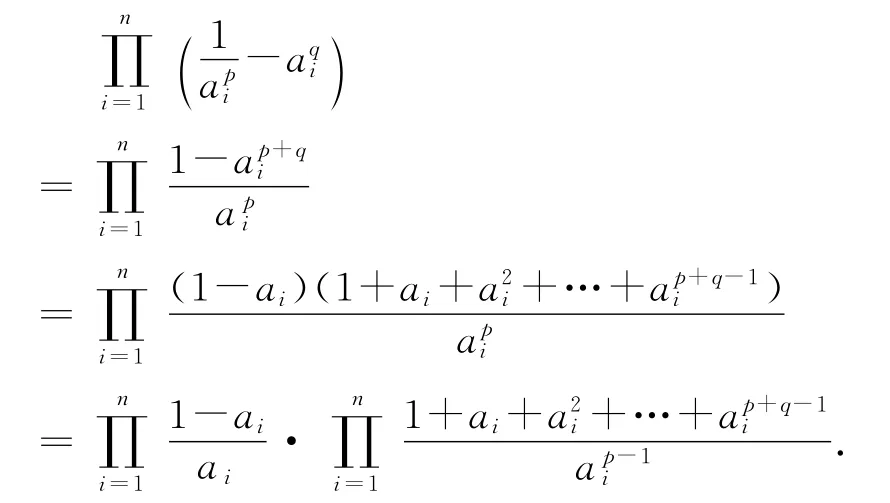
利用算術—幾何均值不等式，有

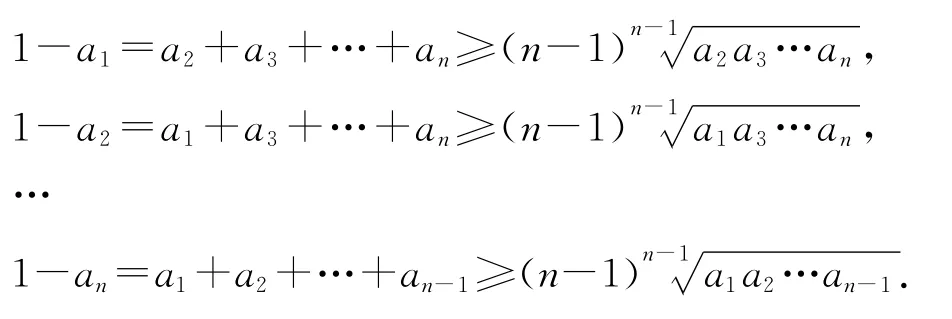
將上述n各不等式相乘，得

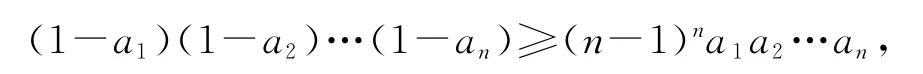
即

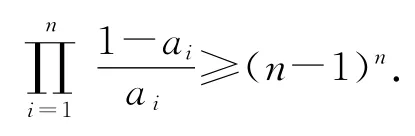
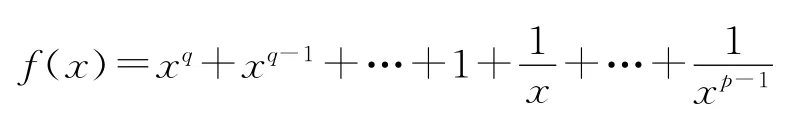
其中s是（*）式中應用算術—幾何均值不等式的乘積項數，u，v，w分別是根號下的正冪指數，所以

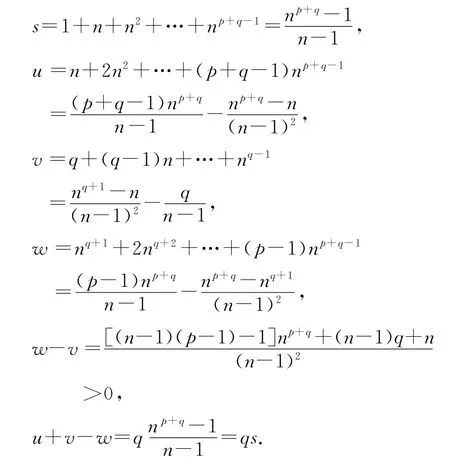
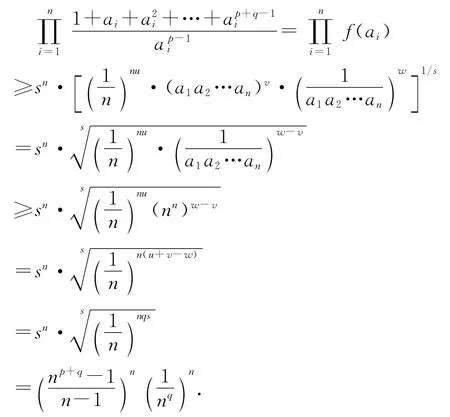
所以

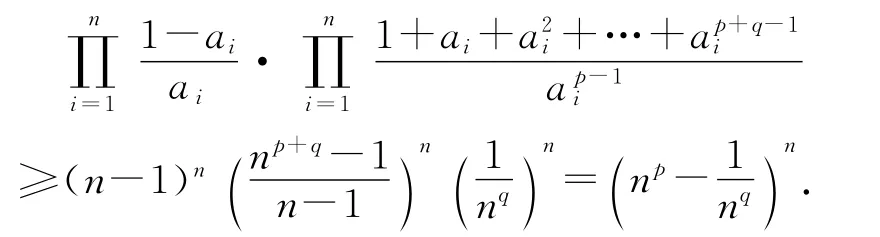
（6）式成立.

由算術—幾何均值不等式等號成立的條件知，（6）式等號成立當且僅當時，證畢.