數(shù)學(xué)問題解答

2017年8月號問題解答

（解答由問題提供人給出）

2376某委員會開了40次會議，每次有10人出席，而且委員會任兩個成員都未在一起出席過一次以上的會議，證明：該委員會成員一定至少有82人.

（浙江省富陽市第二中學(xué) 許康華 311400；浙江省富陽市永興中學(xué) 段春炳 311400）

證明設(shè)該委員會有n成員，用n個頂點u1，u2，…，un表示這n個成員，用40個頂點v1，v2，…，v40表示40次會議，如果成員ui出席會議vj則在頂點ui與頂點vj之間連一條邊，否則，在其他兩頂點之間都不連邊，這樣得到一個二部圖G，則圖G的頂點集為U∪V，其中U=｛u1，u2，…，un｝，V=｛v1，v2，…，v40｝，邊數(shù)為400.因此有.

對于任意的頂點ui∈U，與ui相鄰的頂點對有個.由于任兩個成員都未在一起參加過兩次不同的會議，所以圖G中沒有四邊形，因此，當ui在U中變化時，所有的頂點對都是互不相同的，否則，點對分別在中被計算，那么ui，vk，uj，vl就組成一個四邊形.所以

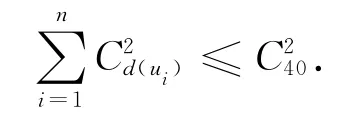
由柯西不等式，有

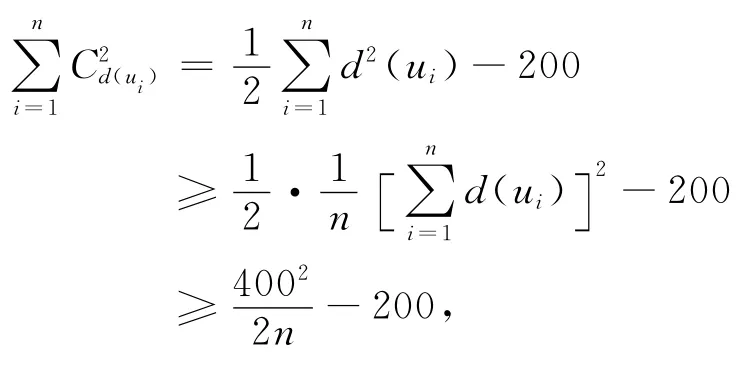
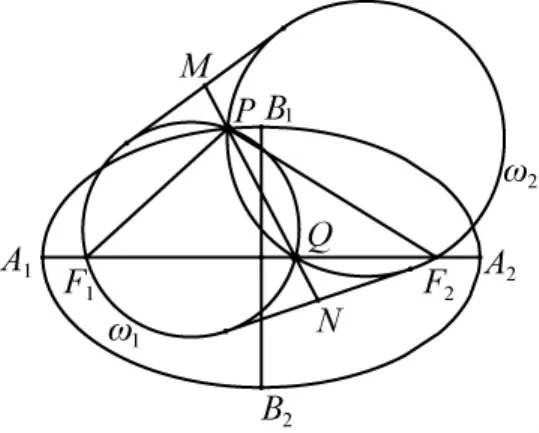
23 77 設(shè)橢圓的長軸為A1A2，短軸為B1B2，焦點為F1和F2，P為橢圓上異于其頂點的任意一點，Q為線段F1F2上異于其端點的任意一點，ω1，ω2分別為△F1PQ和△F2PQ的外接圓，M，N分別為直線PQ與ω1，ω2的兩條外公切線的交點，求證：.

（河南省輝縣市一中 賀基軍 453600）

證明如圖1，設(shè)兩圓ω1，ω2的圓心分別為O1，O2，兩圓的公共弦PQ與直線O1O2的交點為R，點M所在的外公切線與兩圓ω1，ω2的切點分別為M1，M2.

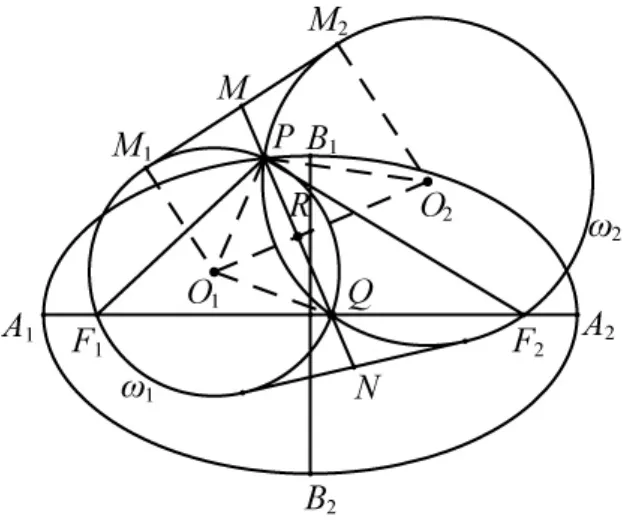
圖1

根據(jù)對稱性可知，直線O1O2同時為線段PQ和線段MN的垂直平分線，其垂足為R.

故MM1=MM2，M為線段M1M2的中點.

連接PO1，PO2和QO1.

又同理得 ∠PO2O1=∠PF2F1，

故△PO1O2∽△PF1F2，

因點P異于橢圓的頂點，故PF1≠PF2，這里不妨假設(shè)PF1＜PF2，從而有PO1＜PO2，即圓ω1的半徑小于圓ω2的半徑.

連接O1M1，O2M2，則O1M1⊥M1M2，O2M2⊥M1M2，四邊形M1O1O2M2為直角梯形.作該梯形的高O1H及中位線MK，如……