由一道課本習題說起

茅雅琳

[摘 要] 教材是教學的依據，作為教師，要把握好教材的編寫意圖和教學內容的教育價值，更要注重對教材進行深度加工和二度開發，充分發揮各種課程資源對促進學生發展的作用. 課堂上，教師要幫助學生成為“知識的建構者”，要引導學生與教材展開“對話”.

[關鍵詞] 研讀教材；運用教材；激發潛能

緣起

教授完人教版《數學》（八上）“12.2三角形全等”一節后，筆者布置書本有關習題進行鞏固練習，有個學生突然喊道：“怎么又是這個圖形！”

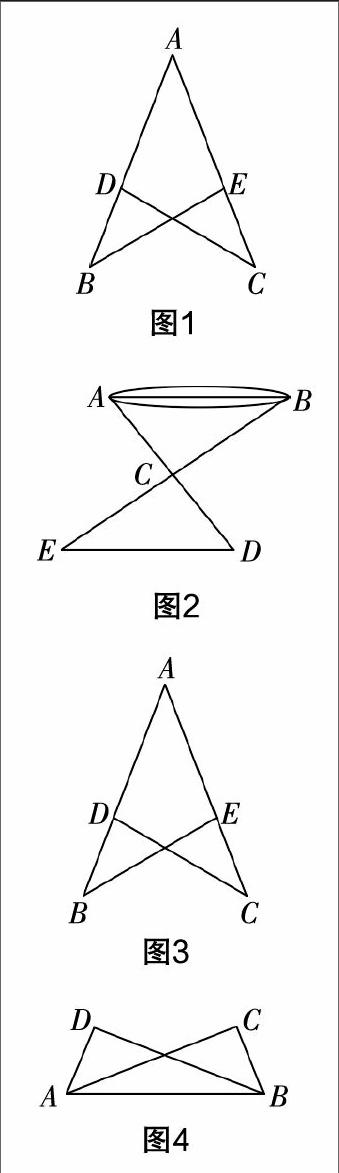
這是教材第43頁習題中的第2題：如圖1，AB=AC，AD=AE，求證∠B=∠C.

確實，在全等三角形這個章節中，共有14道與它類似的題目，它們分別為“12.1全等三角形”中的練習第1題，習題12.1中的第6題，“12.2三角形全等的判定”中的例2、例3和例5，練習中的第2題，習題12.2中的第2，3，6，8，10，12題，習題12.3中的第2題和復習題12中的第4題，這些題目的圖形都可以看成是由這個圖形變化而來的.為什么會有這么多相似的圖形呢？

題目研究

（以教材中出現的三道例題為例）

1. 題目再現

（教材P38例2）如圖2，有一池塘，要測池塘兩端A，B的距離，可先在平地上取一個可以直接到達A和B 的點C，連接AC并延長到點D，使CD=CA，連接BC并延長到點E，使CE=CB. 連接DE，那么量出DE的長就是A，B的距離. 為什么？

（教材P40例3）如圖3，點D在AB上，點E 在AC 上，AB=AC，∠B=∠C. 求證：AD=AE.

（教材P42例5）已知：如圖4，AC⊥BC，BD⊥AD，垂足分別為C，D，AC=BD. 求證：BC=AD.

2. 筆者思考

三道例題放在相應位置的目的有以下三個.

（1）感悟借助新知指導生活實際

新課標十分重視數學與生活的聯系，指出：“學生的數學學習內容應當是現實的，有意義的，富有挑戰性的. ”“教材所選擇的素材應盡量來源于自然、社會中的現象和問題……以使學生感受到數學的價值和趣味. ”本節內容同樣與生活實際密切相關，教材通過利用全等來解決生活中測量池塘寬度的問題，讓學生感受到全等三角形在生活中的實際應用. 其實，測量池塘寬度的問題在本章的習題中還會出現，在后續的相似三角形、解三角形中，學生會接觸到用不同的方法進行測量，將會體會到同一個問題可以有不同的解決方法.

（2）示范運用全等解決數學問題

中學階段重點研究的兩個平面圖形間的關系是全等和相似，而全等的內容是學生學習相似三角形的重要基礎. 為了降低學生利用全等三角形的知識進行推理論證的難度，教材設置了多道例題做出示范，其中例2已知兩邊及夾角對應相等，證第三邊相等，是SAS的簡單運用，例3已知兩角及夾邊對應相等，證另一邊相等，是ASA的簡單運用，而例5是已知直角邊與斜邊對應相等，證第三邊相等，是HL的簡單運用. 以上例題的設置，均是幫助學生運用全等解決數學問題.

（3）初識借助圖形挖掘隱含信息

在數學解題過程中，常需要挖掘題中的隱含條件，以幫助解題. 而人教版教材首次出現隱含條件就在此處，三道例題分別提供了對頂角相等、公共角相等及公共邊相等這樣的隱含條件，借助這三道例題，讓學生學會挖掘圖形中的隱含信息，為解決問題收集足夠的條件.

課堂實錄

學生提出這個問題，說明在不斷的練習中，他們也已經感覺到了這些題目之間的內在聯系. 為了充分發揮本題的教學價值，筆者對本題的教學進行了精心設計，以下為課堂實錄.

引例 如圖5，OD=OE，∠D=∠E，求證：△BDO≌△CEO.

學生很快利用ASA證得兩個三角形全等.

師：如果我們把題目改成“已知OD=OE，______，求證：△BDO≌△CEO”，請小組合作，看看添上哪些條件可使結論仍成立.

（交流5分鐘）

生1：添上∠B=∠C，利用AAS證明.

生2：添上OB=OC，利用SAS證明.

生3：添上BD=CE……不行.

生4：一共就3種添條件的方法.

師：怎樣尋找可以添加的條件？又是怎樣判斷對錯的？說說你的思路.

生4：已知一邊及對頂角相等，還需要尋找一個條件，尋找一邊或者一角.

生3：找邊要注意必須滿足SAS，使已知相等的角成為夾角，我剛才找的BD=CE，就不符合條件.

生5：所以，添上一個條件后，要進行驗證.

生6：還可以將題目改成“已知______，∠D=∠E，求證：△BDO≌△CEO”. 請同學們試試.

生7：我發現這題有三種添法，只要任意添上一條邊就可以了.

生8：因為已知兩對角分別相等，只要任意一對邊相等，都可以證得三角形全等，添上角就不能證明.

師：剛才的幾位同學都善于思考和總結，同學6還提出了有價值的問題. 對于這道題的研究，同學們還有其他的想法嗎？

生9：剛才我們用很多方法證得△BDO≌△CEO，在此基礎上，我們能否對圖形進行變式？我覺得應該可以發現一些新的結論.

同學們按照他的建議，進行嘗試.

（10分鐘后）

生10：如圖6，我們組延長BD，CE交于點A，發現△ABE≌△ACD.

生11：如圖7，我們組連接BC，發現△DBC≌△ECB.

生12：如圖8，他們兩組的圖形結合起來，發現這個圖形中有三組全等三角形.

生13：這三組三角形中，以一組全等為已知，可以證得剩下的兩組均全等.

生14：我剛才連接AO，如圖9，發現還可以證得AO是角平分線.

不需要老師提醒，同學們興致勃勃地開始證明.

師：同學們都善于思考，提出了很多有價值的問題，并進行了積極的探究. 對于以上圖形，我們可以發現一個共同特征，也就是它們都是軸對稱圖形，由對稱性可知，同學們的結論都是正確的.

點評 教師以簡單問題引入，通過示范性變式訓練，激發學生的探究熱情，學生通過改變條件、改變圖形等，衍生出近10道題目，其實質是將相關問題進行整合，在變式訓練的過程中充分發揮本題的教學功能.

教后反思

1. 認真研讀教材，挖掘教育價值

教材是教學的依據，作為教師，要把握好教材的編寫意圖和教學內容的教育價值. 本題類似的圖形在一章中出現了14處之多，并非編寫者簡單的堆砌，而是通過不斷地變換條件和結論，進一步培養學生的推理論證能力，主要包括用分析法分析條件和結論的關系，用綜合法書寫證明格式，以及掌握證明幾何命題的一般過程. 這樣的安排為學生學習后續知識，特別是相似三角形的學習打下了扎實的基礎.

2. 靈活運用教材，發揮教學功能

教師要注重對教材進行深度加工和二度開發，充分發揮各種課程資源對促進學生發展的作用. 教師要幫助學生成為“知識的建構者”，引導學生與教材展開“對話”. 教學時，教師從最簡單的問題入手，通過不斷的變式訓練，使不同的學生得到不同的訓練. 更可貴的是，問題的變式過程全部由學生完成. 愛因斯坦曾說：“提出一個問題往往比解決一個問題更為重要，因為解決一個問題也許只是一個數學上或實驗上的技巧問題. 而提出新的問題、新的可能性，從新的角度看舊問題，卻需要創造性的想象力，而且標志著科學的真正進步. ”在課堂實錄中，學生通過解決老師和同伴提出的問題，進一步加深了對全等三角形判定的理解，同時也提高了學生提出問題、分析問題和解決問題的能力.

3. 無限信任學生，激發學習潛能

新課標明確指出：為了適應時代發展對人才培養的需要，數學課程還要特別注重發展學生的應用意識和創新意識. 試上本課時，變式訓練均由教師給出，學生顯得被動又忙亂，教學效果欠佳，第二節課，如上述課堂實錄所示，學生在火熱的思考中逐漸展開系列變式，結果生14還連接線段AO，帶動問題向縱深處發展. 其實，每個學生都有無限的潛能，只要我們給他們時間、空間，給他們自主思考的機會，他們就會回報給我們驚喜.

結束語

有時，教師為了體現“用教材教”，往往會對教科書內容進行隨意調整，其實這是對“用教材教”的一種曲解. 一套教材代表著一種理念和實踐方法，教師應站在編者角度認真鉆研教材，努力理解和領會教材編寫者的設計理念及教學思想，把握其特點，使教材文本所潛藏的資源得到充分挖掘.