開(kāi)闊視野，呈現(xiàn)新知

萬(wàn)霞

[摘 要] 對(duì)新知教學(xué)的有效方式進(jìn)行探索，是初中數(shù)學(xué)教學(xué)所應(yīng)重點(diǎn)關(guān)注的課題. 創(chuàng)新新知教學(xué)方式的關(guān)鍵在于教學(xué)視野的開(kāi)拓. 從教學(xué)設(shè)計(jì)的角度來(lái)講，這主要是對(duì)教師們提出的要求. 為了實(shí)現(xiàn)富有實(shí)效而又靈活創(chuàng)新的新知教學(xué)，教師們需要解放固有的教學(xué)思維，不斷開(kāi)拓教學(xué)視野，考慮多方影響因素，打造多維度的數(shù)學(xué)教學(xué)過(guò)程.

[關(guān)鍵詞] 初中數(shù)學(xué)；新知教學(xué)；創(chuàng)新方式

數(shù)學(xué)學(xué)習(xí)是一個(gè)不斷遇見(jiàn)新知、理解新知并深化新知的過(guò)程，對(duì)新知識(shí)的接受和處理效果，直接關(guān)系到整個(gè)學(xué)習(xí)效果的理想與否. 初中是數(shù)學(xué)知識(shí)學(xué)習(xí)的基礎(chǔ)階段，這個(gè)時(shí)期知識(shí)內(nèi)容的學(xué)習(xí)質(zhì)量更關(guān)乎日后數(shù)學(xué)能力建立發(fā)展的狀態(tài). 因此，對(duì)于新知教學(xué)的有效方式進(jìn)行探索，是初中數(shù)學(xué)教學(xué)所應(yīng)重點(diǎn)關(guān)注的課題. 通過(guò)對(duì)當(dāng)前新知教學(xué)現(xiàn)狀進(jìn)行調(diào)研，筆者發(fā)現(xiàn)，教學(xué)動(dòng)作雖然井然有序，卻也略顯固化，尤其是在一些難度較大內(nèi)容的教學(xué)過(guò)程中，很難將學(xué)生的思維熱情調(diào)動(dòng)起來(lái)，使教學(xué)效率有待提升. 由此，這種教學(xué)方式的創(chuàng)新顯得十分必要.

運(yùn)用“交流互動(dòng)型”教學(xué)法，激

活學(xué)習(xí)熱情

無(wú)論當(dāng)前的教學(xué)內(nèi)容是什么，來(lái)自學(xué)生心底的學(xué)習(xí)熱情始終是推動(dòng)學(xué)習(xí)活動(dòng)高效進(jìn)行的根本動(dòng)力. 因此，在每一次新知教學(xué)開(kāi)始之初，激活學(xué)生的學(xué)習(xí)熱情都是活動(dòng)開(kāi)展的第一步. 從心理特點(diǎn)上來(lái)講，初中階段的學(xué)生喜好生動(dòng)熱鬧的教學(xué)氛圍. 如果能夠?qū)⒄n堂教學(xué)氣氛向這一方向打造，必將讓學(xué)生在心理動(dòng)力之下完成優(yōu)質(zhì)學(xué)習(xí).

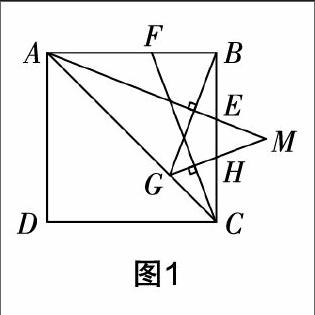
例如，在對(duì)平面幾何的內(nèi)容進(jìn)行綜合講解時(shí)，筆者向?qū)W生提出了這樣一個(gè)問(wèn)題：如圖1，四邊形ABCD是正方形，點(diǎn)E和點(diǎn)F分別在邊BC和AB上，BE和BF等長(zhǎng). 過(guò)點(diǎn)B作AE的垂線，與AC交于點(diǎn)G，再過(guò)點(diǎn)G作CF的垂線，與BC交于點(diǎn)H，點(diǎn)M是AE的延長(zhǎng)線與GH延長(zhǎng)線的交點(diǎn). （1）求證：∠BFC=∠BEA；（2）求證：MA=BG+MG. 這道題雖然比較綜合，涉及正方形、全等三角形等多個(gè)平面幾何知識(shí)，但是，筆者并沒(méi)有直接給學(xué)生揭曉答案，而是請(qǐng)大家自由討論，尋找解答方法. 第一問(wèn)的解答并不困難，到了第二問(wèn)，學(xué)生們的討論愈發(fā)熱烈起來(lái)了. 在大家的思維碰撞和筆者的適時(shí)提示之下，學(xué)生們成功地找到了連接DG構(gòu)造輔助線的方法. 這個(gè)交流互動(dòng)的過(guò)程當(dāng)中，大家不僅體會(huì)到了輔助線構(gòu)造的解題方式，更表示應(yīng)當(dāng)將之進(jìn)行條理化的總結(jié)，幫助日后綜合性問(wèn)題的解答.

“交流互動(dòng)型”教學(xué)法的核心在于為學(xué)生提供了一個(gè)廣闊的自由思考空間. 雖然教師主導(dǎo)能夠更好地保證教學(xué)方向沒(méi)有偏離，但是，也很容易讓整個(gè)課堂氣氛陷入凝固、死板的境地. 教師們應(yīng)當(dāng)認(rèn)識(shí)到，交流互動(dòng)并不是課堂教學(xué)的全部，而是在教師的適時(shí)引導(dǎo)中穿插進(jìn)行的. 教師引導(dǎo)的存在，使得交流互動(dòng)不會(huì)偏離主題；而交流互動(dòng)的存在，也使得課堂教學(xué)不致枯燥乏味.

運(yùn)用“探究參與型”教學(xué)法，有

效靈活思維

初中數(shù)學(xué)知識(shí)內(nèi)容并不是浮于表面的，而是具有很多拓展深入的可能性. 只有意識(shí)到這些可能性，并將它們抓住，才能將數(shù)學(xué)教學(xué)的效能發(fā)揮到最大. 為了將數(shù)學(xué)知識(shí)的內(nèi)涵全部發(fā)掘出來(lái)，需要從基礎(chǔ)知識(shí)表面入手，開(kāi)展靈活深入的探究，以全面的視角觀察數(shù)學(xué)，從而收獲最為有效的數(shù)學(xué)學(xué)習(xí).

例如，在對(duì)函數(shù)與幾何內(nèi)容進(jìn)行教學(xué)時(shí)，筆者發(fā)現(xiàn)，在深入探究的過(guò)程當(dāng)中，二者存在著相交之處. 為了盡可能地延伸學(xué)生的思維路徑，筆者特意設(shè)計(jì)了這樣一道習(xí)題：如圖2，Rt△AOB位于一個(gè)平面直角坐標(biāo)系當(dāng)中，其中點(diǎn)A是第一象限內(nèi)的點(diǎn)，∠A是直角，∠AOB=60°，OB=2，且在x軸的正半軸上，OC是∠AOB的平分線，與AB交于點(diǎn)C. 現(xiàn)有一動(dòng)點(diǎn)P，按照B—C—O的方向以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng)，共運(yùn)動(dòng)t s. 與此同時(shí)，另一個(gè)動(dòng)點(diǎn)Q按照C—O—y的方向以每秒1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng)，并在點(diǎn)P運(yùn)動(dòng)到點(diǎn)O時(shí)同時(shí)結(jié)束運(yùn)動(dòng). （1）OC和BC的長(zhǎng)分別是多少？（2）若記△CPQ的面積是S，則S與t之間存在怎樣的函數(shù)關(guān)系？（3）如圖3，當(dāng)兩個(gè)動(dòng)點(diǎn)運(yùn)動(dòng)時(shí)，PQ與OA相交于點(diǎn)M，那么，若要使△POM是等腰三角形，t應(yīng)當(dāng)取何值？這樣一系列問(wèn)題，學(xué)生在兩種知識(shí)的結(jié)合之中體驗(yàn)到了一次綜合完整的知識(shí)探究，并很好地將代數(shù)與幾何知識(shí)結(jié)合了起來(lái).

從探究活動(dòng)的靈活性與自發(fā)性等特點(diǎn)來(lái)看，學(xué)生應(yīng)當(dāng)成為數(shù)學(xué)知識(shí)探究的主體. 只有當(dāng)學(xué)生真正參與進(jìn)來(lái)之后，他們才能感知到數(shù)學(xué)知識(shí)的靈動(dòng)發(fā)展，并在發(fā)現(xiàn)新知的同時(shí)開(kāi)拓思維. 這種思維層面上的優(yōu)化，對(duì)于數(shù)學(xué)學(xué)習(xí)的長(zhǎng)遠(yuǎn)發(fā)展都具有重要意義.

運(yùn)用“媒體輔助型”教學(xué)法，深

入剖析知識(shí)

隨著時(shí)代的不斷發(fā)展，初中數(shù)學(xué)教學(xué)也在經(jīng)歷著方式方法上的持續(xù)變革. 與以往的單純講述相比，多媒體的介入使得課堂教學(xué)煥發(fā)出了全新的活力. 一方面，新鮮的教學(xué)形式為學(xué)生點(diǎn)燃了高漲的學(xué)習(xí)熱情. 另一方面，很多復(fù)雜晦澀的知識(shí)內(nèi)容在多媒體全面、靈活的展現(xiàn)之下變得細(xì)致、清晰了許多，這對(duì)于數(shù)學(xué)知識(shí)的剖析來(lái)講，意義重大.

例如，在對(duì)正方形內(nèi)容進(jìn)行教學(xué)時(shí)，為了能夠讓學(xué)生將正方形的性質(zhì)特點(diǎn)體會(huì)到位，筆者向大家提出了這樣一個(gè)問(wèn)題：現(xiàn)有一個(gè)正方形ABCD，若將其中的點(diǎn)C固定，并繞著點(diǎn)C將這個(gè)正方形進(jìn)行旋轉(zhuǎn)，成為正方形A′B′CD′，其中A′B′與AD交于點(diǎn)E，∠B′CB=30°，那么，AE的長(zhǎng)度是多少？?jī)H從文字表面上來(lái)看，剛剛接觸正方形知識(shí)不久的學(xué)生很難發(fā)現(xiàn)其中隱藏的規(guī)律. 于是，筆者打開(kāi)電腦中的“幾何畫(huà)板”軟件，依照已知條件中的敘述將圖形畫(huà)出來(lái)，并運(yùn)用其中的動(dòng)畫(huà)功能將正方形旋轉(zhuǎn)的過(guò)程進(jìn)行清晰演示（如圖4）. 操作雖然簡(jiǎn)單，但在這樣的反復(fù)演示之下，學(xué)生得以明確觀察到其中哪些量變化了，哪些量沒(méi)有變，進(jìn)而發(fā)現(xiàn)正方形性質(zhì)的存在，實(shí)現(xiàn)了知識(shí)內(nèi)容的準(zhǔn)確理解.

根據(jù)不同類(lèi)型多媒體的呈現(xiàn)特點(diǎn)，其所適用的教學(xué)內(nèi)容也存在一定的差異. 如果教學(xué)目的在于激發(fā)學(xué)生的思考興趣，教師往往可以選擇具有聲、光表現(xiàn)能力的多媒體形式. 而如果教學(xué)目的在于闡明知識(shí)內(nèi)容本身，教師便可以選擇具有圖形或動(dòng)畫(huà)表現(xiàn)能力的多媒體，化抽象為具體. 無(wú)論怎樣，多媒體的介入輔助，都為初中數(shù)學(xué)知識(shí)的深入剖析注入了一劑強(qiáng)勁動(dòng)力.

運(yùn)用“學(xué)以致用型”教學(xué)法，理

論聯(lián)系實(shí)際

在初中數(shù)學(xué)知識(shí)的學(xué)習(xí)過(guò)程當(dāng)中，僅有理論層面的探究是遠(yuǎn)遠(yuǎn)不夠的. 只有成功地將理論知識(shí)與實(shí)際應(yīng)用聯(lián)系起來(lái)，做到以數(shù)學(xué)理論解決實(shí)踐問(wèn)題，才能被評(píng)價(jià)為將數(shù)學(xué)知識(shí)學(xué)懂了. 這種學(xué)以致用的思維路徑應(yīng)當(dāng)普遍存在于整個(gè)數(shù)學(xué)知識(shí)學(xué)習(xí)過(guò)程當(dāng)中. 因此，以之作為新知教學(xué)的重要方法，幫助學(xué)生在初中階段建立起這種有效的思維習(xí)慣，對(duì)于數(shù)學(xué)學(xué)習(xí)來(lái)講非常重要.

例如，在對(duì)函數(shù)內(nèi)容進(jìn)行教學(xué)時(shí)，筆者大膽加入了如下思考題：某水果店想要開(kāi)始銷(xiāo)售太陽(yáng)果，并通過(guò)市場(chǎng)調(diào)查得出了下表中的銷(xiāo)售規(guī)律. 若太陽(yáng)果的進(jìn)價(jià)是20元/千克，為了獲得最大利潤(rùn)，應(yīng)當(dāng)將其單價(jià)由40元/千克下調(diào)到多少元？實(shí)際問(wèn)題的出現(xiàn)，立刻拓寬了學(xué)生的思維視野，在解題的同時(shí)，大家對(duì)于函數(shù)的認(rèn)知也更加靈活、深刻了.

不難發(fā)現(xiàn)，以學(xué)以致用的方式呈現(xiàn)數(shù)學(xué)新知的操作過(guò)程并不復(fù)雜. 實(shí)際上，在初中數(shù)學(xué)的各類(lèi)測(cè)試當(dāng)中經(jīng)常出現(xiàn)的應(yīng)用性問(wèn)題，就是這一教學(xué)思想的集中體現(xiàn). 如果在新知呈現(xiàn)階段便引導(dǎo)學(xué)生主動(dòng)將之聯(lián)系到實(shí)際生活當(dāng)中，便可以在教學(xué)開(kāi)始之初觸發(fā)大家學(xué)以致用的思維方向，為深入、有效理解知識(shí)埋下伏筆.

創(chuàng)新新知教學(xué)方式的關(guān)鍵在于教學(xué)視野的開(kāi)拓. 從教學(xué)設(shè)計(jì)的角度來(lái)講，這主要是對(duì)教師們提出的要求. 為了實(shí)現(xiàn)富有實(shí)效而又靈活創(chuàng)新的新知教學(xué)，教師需要解放固有的教學(xué)思維，不斷開(kāi)拓教學(xué)視野，考慮多方影響因素，打造多維度的數(shù)學(xué)教學(xué)過(guò)程. 在這樣的創(chuàng)新教學(xué)體系下，學(xué)生得以感受到煥然一新的學(xué)習(xí)氛圍，并在全新的教學(xué)模式之下感受到初中數(shù)學(xué)的新面貌.