例談“變式”在初中數學課堂教學中的妙用
謝小兵
[摘 要] 變式教學是初中數學教學中常用的一種教學策略. 這種策略不僅可以使新知識和學生已有認知結構之間建立起一種實質性的聯系,而且有利于學生數學思維品質的培養,有利于學生全方位、多角度地理解和應用新知識. 數學概念變式、數學方法變式、數學應用變式是變式教學的三種方法.
[關鍵詞] 變式教學;數學概念變式;數學方法變式;數學應用變式
在數學教學中,所謂“變式”就是在保持本質特征不變的情況下,對于數學概念、法則、公式以及定理從多個角度、背景、層次探索其本質屬性的過程. 在新課標理念下,探討“變式教學”,不僅可以促使學生透過現象看到題目考查的本質,使新知識和學生已有認知結構之間建立起一種實質性的聯系,而且也有利于學生數學思維品質的培養,有利于學生全方位、多角度地理解和應用新知識. 本文以蘇教版初中數學教材為例,從概念變式、方法變式以及應用變式三個方面進行研究.
數學概念變式
對于初中生而言,數學概念是一個比較抽象且難以理解的問題,常常是通過記憶的形式進行理解,一旦在具體解題過程或者是運用概念進行判斷時學生常常出現錯誤. 因此,教師在組織學生學習一個新概念后,應通過多層次、全方位、多角度的概念變式引導學生探尋該概念的本質,使學生更加準確地理解相關概念的內涵和外延,從而幫助學生形成完整清晰的概念.
1. 概念引入變式
概念的引入是概念形成的基礎,教師應通過客觀現象抽象的方式,充分展示知識形成的過程,增強本質屬性與非本質屬性的對比度. 如在八年級數學下冊學習平行四邊形概念時,教師務必借助粉筆盒、教室窗戶、數學課本、伸縮推拉門等參照物的一個表面進行引入,探討出每一實例圖形的屬性,抽象歸納出平行四邊形的本質屬性,進而得到平行四邊形的定義,這種概念的引入方式,不僅讓學生準確掌握了平行四邊形的具體含義,而且也有利于正方形、長方形等平行四邊形特殊形式的學習.
2. 概念辨析變式
在概念引入后,為了能夠深化理解、明確概念的本質,教師要根據概念的內涵與外延及時設計出辨析型問題,讓學生直接運用概念作出判斷和解答,讓學生熟悉概念. 如在八年級數學下冊引入反比例函數概念后,教師可及時組織學生探討下列8項中哪些是反比例函數.
3. 概念深化、固化變式
在概念辨析變式中,學生是通過直接運用概念進行判斷和解答的,但是實際做題過程中,常常出現概念的等價形式,此時,教師應組織學生進行概念等價形式的探討,切實達到靈活應用概念、透徹理解概念的目的. 例如,在七年級數學下冊學習一次函數y=kx+b(k≠0,且k,b均為常數)的概念后,教師可引導學生深入探討以下問題:(1)若k=0,則這個函數是什么函數;(2)若b=0,則這個函數又是什么函數. 通過這些變式題目的訓練,可以讓學生發現問題本質,更加深入地理解常數函數、一次函數等具體概念.
數學方法變式
數學題目是數學思想、方法和知識的載體,面對繁多的數學題目,不僅要讓學生學會具體題目的解題方法,而且要在習題的解決過程中形成構建數學經驗體系,達到訓練思維、總結規律、以不變應萬變的教學目的.
1. 一題多解
對于同一事物,不同的人有著不同的看法,同理,對于同一數學問題,不同的學生有著不同的解法. 因此,教師應引導學生在自己力所能及的知識范圍內應用發散思維,提出不同的解題方法,從而達到活躍思維、綜合運用知識的目的.
例如,在八年級數學上冊學習等腰梯形時,教材中對于等腰梯形判定定理的證明方法較為簡單,教師應結合已學知識引導學生思考更多的做題方法.
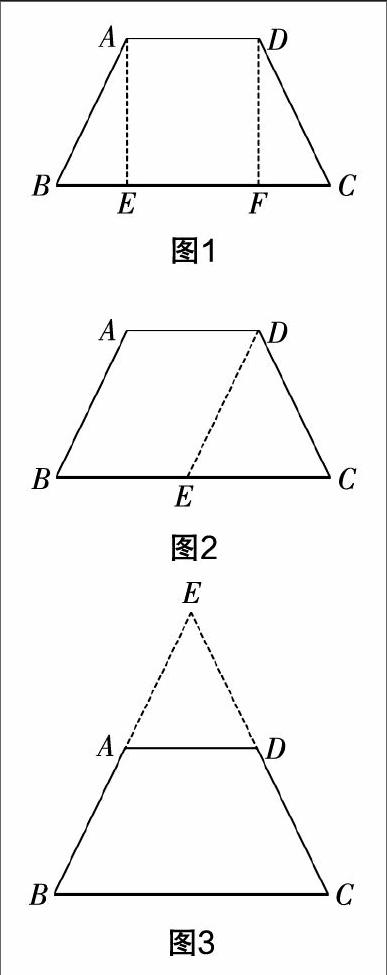
第一種方法:如圖1所示,作DF,AE垂直于BC,并與BC分別相交于點F和點E,通過角角邊判定定理,得到△ABE和△DCF全等,最后利用全等三角形的性質得到AB=CD.
第二種方法:如圖2所示,作DE∥AB交BC于E,利用平行線的性質得到∠B=∠DEC,利用等角對等邊的性質推出DE=DC,再利用平行四邊形的性質得到AB=DE,最后利用等式的性質得到AB=CD.
第三種方法:如圖3所示,延長BA,CD,交于點E,利用等角對等邊的性質,得到BE=CE,AE=DE,從而利用EB-EA=EC-ED,得到AB=CD.
值得一提的是,一題多解對于教師和學生的要求普遍較高,并不要求學生掌握所有的方法,而是要在多種解題方法過程中善于總結,不斷拓寬學生的解題思路,從多種解題方式中選擇出適合自己的最優解題方法.
2. 一題多變
在規律的形式化歸納過程中,學生對于形式化的數學知識普遍感到困難,因此,教師應從設計變式教學環節,對某一題目進行條件變換,借助變式多角度地探討數學規律,從而達到觸類旁通、舉一反三,提高學生學習效率的目的.
例如,在九年級數學下冊學習二次函數圖像時,首先通過描點的方式畫出y=x2和y=2x2的圖像,總結出圖像的開口方向、頂點坐標、對稱軸等變化規律;其次,通過描點的方式嘗試驗證y=2x2和y=-2x2,總結出圖像的開口方向、頂點坐標、對稱軸等變化規律,引導學生觀察圖像和二次函數系數的不同,得出圖像的開口方向與二次函數系數之間的關系,即二次函數y=ax2,當a>0時,圖像開口向上;當a<0時,圖像開口向下.
3. 多題一解
在教學或者習題訓練中,我們不難發現許多題目的解題方法具有某種共性,常常在內容上相互轉換和滲透. 因此,教師應區分異同,增強學生思維的廣闊性和深刻性,使知識系統化. 同時,多題一解變式也包括等價命題、逆否命題、不同題型之間的轉換. 通過這種多題一解變式,有利于培養學生知識的正向遷移能力,達到數學練習“萬變不離其宗”的目的,
例如,若使方程x2-(a-2)x+4=0有實根,則a的取值范圍是什么?對于這一題目可從多個角度進行分析.
從不等式的角度分析,可轉換為:若使x2-(a-2)x+4<0的解集非空,則a的取值范圍是什么?
從二次函數的角度分析,可轉換為:若使二次函數y=x2-(a-2)x+4與x軸有交點,則a的取值范圍是什么?
從二次三項式的角度分析,可轉換為:若使二次三項式x2-(a-2)x+4能分解為兩個不同因式的積,則a的取值范圍是什么?
其實,上述四個題目均為等價命題,其解題方式一致,要引導學生從多個角度進行分析.
數學應用變式
知識的學習和應用是高度統一的. 《數學課程標準》明確指出:對于初中數學知識的學習,不僅要知道是什么、為什么的問題,而且還需要學會運用數學的思維方式解決實際生活中的問題. 數學應用變式的學習,有利于在實際問題面前提高學生的數學應用意識,激發學生學習數學的興趣,并積極探索數學知識的應用價值. 在具體教學實踐中. 初中數學教師務必結合教材,在教材內容選取上要結合初中生的生理和心理水平,不斷改變題目的背景、條件以及結論等,提高學生的創新能力.
例如,七年級數學上冊第100頁習題第5題,這是一個面積問題,可得方程為(12+x)×8=120. 根據該方程,教師可以結合實際問題改變問題產生的背景,變為銷售問題:一套兒童衣服,褲子每條銷售12元,銷售員今天共賣出兒童衣服8套,收到購買款240元,假如每件上衣的價格相等,則每件上衣的銷售價格是多少. 雖然兩題產生的背景各不相同,但所列的一元一次方程是一致的,這樣可以使學生在解決實際問題時抓住問題的關鍵,培養學生思維的靈活性和開放性.
綜上所述,在初中數學課堂教學中,教師應抓住數學問題的本質屬性,通過設計數學概念、數學方法以及數學應用變式,并把它作為一種行之有效的教學方法應用于教學實踐. 只有這樣,才能培養學生的發散思維,引導學生在學習過程中不斷歸納總結,讓枯燥乏味的數學課堂變得生機勃勃.

