淺論教師課堂管理與調控能力的提升
高峰官
[摘 要] 課堂管理與調控行為的好壞,直接影響教學活動,決定教育教學質量的高低. 有效的課堂管理與調控需要師生間的情感互動與智慧生成. 為此,需加強情感交流,活躍課堂氛圍;把握教育智慧,及時化解沖突;以問題驅動為抓手,促進學生學習;暴露思維過程,促進學生反思.
[關鍵詞] 管理與調控;情感交流;教育智慧;問題驅動;暴露思維
教師課堂管理與調控行為的好壞,將直接影響教學活動能否順利進行,決定著教學質量的高低. 如何有效管理與調控,對教師來說非常重要.
教學中,課堂管理問題隨處可見,新教師尤為突出. 教學效果不僅取決于教師怎樣教,學生怎樣學,還取決于一定的教學環境. 課堂管理與調控需要關注師生間的情感交流;關注師生間的互動生成;關注教學智慧的提升;關注學生的思維發展. 有效的課堂管理與調控需要創設一個充滿生機活力的新型課堂.
加強情感交流,活躍課堂氛圍,
有效調控學生學習
課堂是教與學的雙邊活動. 傳統的課堂管理主要采取管、卡、壓的手段控制學生,結果問題越來越多. 為建立積極的課堂氣氛,教師可用以下方法進行管理與調控. 一是以情喚情. 課堂上學生出現思想不集中,低聲講話或做小動作,在所難免. 以情感人、以情管人是解決問題的好辦法. 要從語意到行為都讓學生感到教師在關心他,使其配合管理. 二是輕敲響鼓. 教師在教學中要善用含蓄方法對學生的違紀行為進行誘導和影響. “響鼓不用重錘敲”,學生聽到教師的“弦外之音”,會領會到教師的意圖和良苦用心,做出知心、知情、知理的反映,及時改正錯誤. 三是目光暗示. 人眼為窗,可傳情傳神. 教師課堂上視野所及,可以眉目傳情,促進學生專心聽講. 四是動作指引. 教師課堂上的一顰一笑、舉手投足、面部表情都能傳達管理信息,具有吸引注意力、優化課堂管理的作用.
把握教育智慧,及時化解沖突,
有效管理學生學習
案例1 課堂上學生發生沖突的處理片斷
某老師在讓學生討論問題時,大多數學生都在認真討論,但有兩個男同學不知什么原因,在討論時發生爭執,甚至動起手來,結果全班都停下來. 大家都以為老師要嚴厲批評兩位同學,結果老師悄悄走到這兩位同學身邊,輕輕摸了摸兩位男同學的頭,然后對全班同學說:“我們現在是在討論數學問題,大多數同學采用的是語言交流,這兩位不但用語言交流,還用動作、手語加以交流,下面請兩位同學談一下他們‘手語討論的結果吧. ”這兩人的臉一下子就紅了,老師又說,“我明白了,他們對討論的內容還沒有把握好,想下課當面和老師交流一下. 好,大家繼續討論吧. ”同學們都輕輕笑了,又繼續討論起來.
案例中,這位教師的教學管理經驗非常豐富,折射出其課堂管理的理念和智慧:一,課堂是大家學習的場所,不是幾個人的專場,不能因一兩個學生影響其他人;二,學生是發展中的人,對學生的犯錯,應及時制止,讓其認識錯誤,消除影響,既教育其本人,又教育全班;三,課堂管理是一門藝術,不需暴風驟雨,應學會冷處理,化沖突為和諧,將課堂處理與課后教育結合起來,將沖突轉化為教育管理資源,促進學生的數學學習.
以數學問題驅動為抓手,有效
管理與調控學生的數學學習
1. 把學生當成真正的研究者,讓學生感受知識生成過程
案例2 三角形的高線性質的教學片斷
教學三角形的中線、角平分線和高線時,首先,師生共同探究三角形三條中線相交于三角形內一點,角平分線也交于三角形內一點. 此時,教師讓學生猜想,三條高會怎樣呢?結果大多數學生猜想“三角形的三條高也交于三角形內一點”. 教師笑而不答,讓學生先自行探究,再小組探究,最后讓小組選出代表交流. 一組得出的結論是銳角三角形的三條高交于三角形內一點,另一組得出直角三角形的三條高交于直角頂點,還有一組提出異議——鈍角三角形的三條高不相交,但將高線延長后相交于三角形外一點. 教師肯定了學生的發現,啟發學生:這三種情況能否統一起來?同學們又開始議論,最終共同得出:三角形三條高所在的直線交于一點. 這體現了三角形圖形的內在美.
結論的發現不是教師直接告訴學生的,而是通過巧妙的問題創設、變式拓展,引導學生體驗規律的發現過程. 教師引導學生先研究三角形的三條中線與角平分線,然后讓他們大膽猜想關于三角形三條高的結論. 當學生發現鈍角三角形與猜想不符時,便及時引導學生拓展思路,將三條高改為三條高所在的直線,從而將問題化解,與中線和角平分線共同體現了三角形的內在統一美.
在探究中,教師要把學生當成真正的研究者,讓學生親身感受知識的生成過程. 知識是無法學盡的,我們應教給學生學習策略,讓學生在學習中生成新知識,掌握新技能,獲得情感體驗,為后續學習和終身發展奠定基礎.
2. 以問題變式為驅動器,讓探究活動充滿創新活力
何為創新?曾有一位學者說過:“創新就是將有限的資源進行重新整合. ”對于數學命題來說,能否引導學生將命題題設部分和結論部分進行重新排列,就是創新. 對于一個數學問題來說,將思維背景進行變式,進行類比、聯想和發散,同樣也是思維創新.
案例3 一道數學題的拓展研究
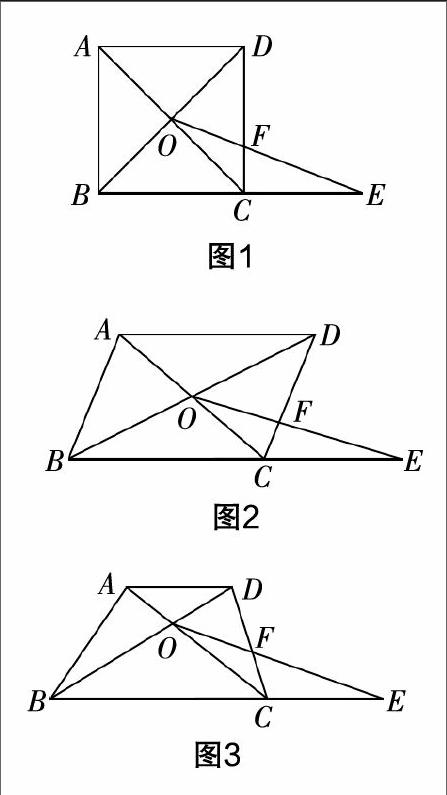
如圖1,四邊形ABCD是正方形,BC =1,對角線的交點記作O,點E是邊BC延長線上一點. 連接OE交CD邊于點F,設CE=x,CF=y,求y關于x的函數解析式.
(1)小明認為可通過添加輔助線——過點O作OM⊥BC,垂足為M求解,你認為這個想法可行嗎?
(2)如果將條件“四邊形ABCD是正方形,BC=1”改為“四邊形ABCD是平行四邊形,BC=3,CD=2,”其余條件不變(如圖2),請你寫出y關于x的函數解析式;
(3)如果將條件“四邊形ABCD是正方形,BC=1”進一步改為“四邊形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c”其余條件不變(如圖3),請你直接寫出y關于x的函數解析式.
案例圍繞四邊形性質與相似等問題,引導學生由淺入深、由特殊到一般進行大膽變式,提出新問題,給學生以機會,讓學生體驗探究與創新的思維歷程,讓學生歸納出一般性方法. 可見,問題的生成是師生共同創設的,這對促進學生的創新思維大有裨益.
以暴露師生思維為策略,有效
管理與調控學生學習
新課程倡導:“教學活動必須以學生發展為本,培養學生學會用數學思維來思考問題,用數學方法解決問題,用數學語言表達數學問題. ”從教學目的來看,學生是學習主體,教師的“教”須通過學生的“學”才能實現學生發展. 學生思維能力的發展,是在暴露和反思中得到錘煉和提高的,對此,可通過案例說明.
案例4 三角形兩邊之和大于第三邊的應用教學片斷
問題:現有兩根木條 a和b,a長10 cm,b長3 cm,如果再找一根木條c,用這三根木條釘成一個三角形,那么對c有什么要求?
先讓學生回想三角形三邊數量關系,然后設木條c的長為x cm,根據三角形三邊關系列出不等式.
通過觀察,學生的做法大略有:(1)一部分列出10+3>x和10-3 在展示基礎上,引導學生進行分析和評價,最后列出課本上呈現的不等式x<10+3,x>10-3. 案例中,因學生知識結構的差別、思維品質的不同,解題方式也不同. 教師先讓學生小組探討,暴露思維過程,而后討論,對各種解法、思維過程及思維品質給予評估,發展學生的反思能力. 教學中,教師將教材安排意圖、自己處理問題的想法剖析出來,便于學生深層次理解與借鑒;學生將自己認識、解決問題的思維曝光,便于教師及時反饋評價與針對性糾錯. 這樣就形成“教”與“學”的回路,有助于學生的思維發展. 總之,教學受教材、教師、學生、媒體、環境等多因素相互影響與作用,是促進學生認知和情感增長的動態過程. 教師有效管理與調控地“教”,最終都要落在“有效學”上. 為此,教師要以學生為中心開展教學,尋找學生思維的“生長點”,讓教學更有效,讓學習更有效.

