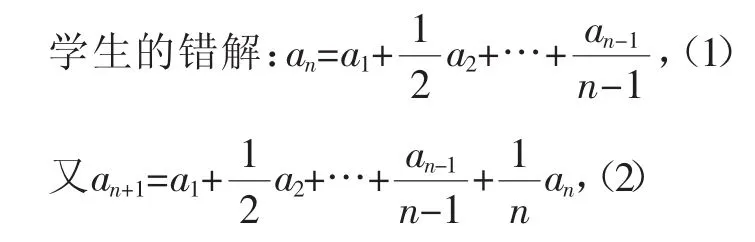嘗試中犯錯、反思 反思中發現、積累
——“嘗試—發現”教學法的靈活運用

☉江蘇省宜興中學 劉國祥

嘗試中犯錯、反思 反思中發現、積累
——“嘗試—發現”教學法的靈活運用

☉江蘇省宜興中學 劉國祥

曾讀過一篇文章，題目叫《教室就是出錯的地方》，作者魏得勝.“教室就是出錯的地方.”這句話說得太好了！細想起來，確實就是這樣.出錯是正常的，不出錯才是不正常的.如果學生的學習解題、所作所為都正確，沒有出錯，教師乃至學校就沒有存在的價值了.從教學的角度看，錯誤是重要的教學資源.任何正確的答案和方式，都是通過曲折探索得到的.而往往在出錯和改錯的曲折探索過程中，課堂才是最活的，教學才是最美的，學生的生命才是最有價值的.從這個意義上說，錯誤對于學生，不是盡量避免的問題，而是不可或缺的元素.關鍵是我們如何對待如何運用這樣的“錯誤”.

高中數學新課程教學中，我們常常引進“嘗試—發現”教學法，即讓學生在老師創設的教學情境下自主嘗試學習，在學習中自主發現、探索，解決數學學習過程中的問題.這種教學方法強調學生主體參與和實踐中完成自身知識建構的發展.但是教學現實中，教師還是不斷給學生詳盡的“提示”，唯恐學生出錯；面對學生的“錯誤”，除批評、責怪，并沒有重視這一重要資源.由此，我將“嘗試—發現”教學法推進一步，形成“嘗試—犯錯—反思—發現—積累”的教學方法，即讓學生在一定的教學情境下自主嘗試學習，在嘗試中犯錯或產生思維阻塞，抓住這個契機，教師引導學生討論反思，尋找錯因，發現正確方法正確思路，在發現中積累經驗與教訓，從而提高數學解題能力.下面以高中數列教學為例說說這種教學方法的意義.

數列是普通高中數學的重要內容，在整個中學數學教學內容中，處于一個知識匯合點的地位，很多知識都與數列有著密切聯系；同時，數列蘊涵了許多重要的數學思想，在數列教學中注重數學思想方法的挖掘與滲透具有十分重要的意義.在高中數學數列教學中，我運用“嘗試—犯錯—發現—積累”教學法，收到顯著效果.

一、利于積累審題經驗

嘗試中犯錯發現細心閱讀題目，正確理解概念，提高運算技能在數學解題中的重要性，從而積累教訓.

故人云“智者千慮，必有一失”.學生解題時經常出現錯誤，并不是方法不對，也不是解題過程不嚴密，常常是因為平時解題時，老師有明確的提示與強調，所以缺乏細心讀題、正確辨析概念的良好習慣，或者是忽略提高運算技能而造成的.

例1求和Sn=a+3a2+5a3+…+（2n-1）an.

錯解1：aSn=a2+3a3+5a4+…+（2n-1）an+1，因此（1-a）sn= a+2a2+2a3+…+2an+（2n-1）an+1（最后一項應是減號）.

錯誤2：（1-a）Sn=a+2a2+2a3+…+2an-（2n-1）an+1，則（中間是n-1項等比數列和，并不是n項等比和）.

錯誤3：沒有對變量a分類討論，分a=0，a=1，a≠0且a≠1三種情況來討論.

解題啟示：概念理解上的偏差是造成學生解題錯誤的常見原因，讓學生自主嘗試解題，然后針對學生錯誤，創設情境討論錯誤原因，讓學生頓悟.上面案例中的錯誤3告訴我們在使用等比數列求和公式時要注意對公比q進行討論；而錯誤一和二關鍵是運算技能的缺失.通過這樣的嘗試、犯錯、發現，逐步培養學生審讀題目、辨析概念與重視運算技能良好習慣.

二、利于培養思維習慣

嘗試犯錯中發現打破習慣思維，研究條件、改變思維角度帶來的意外效果，從而培養審題分析的良好習慣.

對于一題多解的問題，學生往往孤立地看待條件，從而鉆進死胡同，形成繁雜的解題過程，既費時間，又易出錯.如果能夠利用題目條件，改變思維角度，采用簡約的思維，往往可以直達問題的本質，運算更簡單，更能保證解題的正確性.

例2 數列｛an｝成等差數列，S10=100，S100=10，求S110.

解法1：這是我有意讓學生自主嘗試的一道計算題.絕大多數同學想到設首項為a1，公差d聯立方程得得由于運算復雜，結果僅有較少一部分同學能得出S110=-110.

本題是否一定要求出首項和公差呢？在多數同學經歷挫折后，老師適時引導學生改變思維角度，運用整體思維，研究S10和S100間關系，思考另一種解法.結果，有學生發現：

解法2：a11+a12+a13+…+a100=-90得到a11+a100=-2，因此

解題啟示：解法2運算簡單，體現整體思維，事半功倍.學生為什么沒想到后一種方法？原來，學生潛意識里只有求首項和公差，沒想到利用S10和S100之間的關系.面對運算繁雜的解法1，只要稍稍轉換思維角度即可獲得解法2，可見，面對繁雜的運算題，從整體上把握題中條件，研究條件間的聯系，改變思維角度，就可以取得意想不到的解題效果.學生從中積累了經驗，可以很容易完成以下問題：

（1）等差數列｛an｝中，前n項和為Sn，若Sn=m，Sm=n（m≠n），則Sm+n=-（m+n）.

（2）等差數列｛an｝中，前n項和為Sn，若Sn=Sm（m≠n），則Sm+n=0.

（3）等差數列｛an｝中，前n項和為Sn，若Sn=m2，Sm=n2（m≠n），則Sm+n=-（m+n）2.

（4））等差數列｛an｝中，前n項和為Sn，若則

三、利于提高思維的靈活性

嘗試中思路受阻時，發現調整解題角度或解題方法，可以打通思路，積累解題智慧，培養思維的靈活性.

解題中途思維受阻，因而無法完成解題，是學生在數學解題中經常遇到的情況.這時，通過師生共同分析討論思路不通的原因，調整解題方向或解題方法，會讓學生有豁然開朗的感覺.

例3已知兩個等比數列｛an和｛bn｝，滿足a1=a（a>0），b1-a1=1，b2-a2=2，b3-a3=3，若數列｛an｝是唯一，求a值.

學生很容易想到設數列｛an｝的公比為q，由數列（2+ aq）2=（1+a）（3+aq2），得aq2-4aq+3a-1=0.（*）

由a>0得Δ=4a2+4a>0，卻發現方程有兩解，與題中數列｛an｝是唯一發生矛盾而思路中斷.這時師生共同分析思路不通原因，回頭再分析題目，突然發現公比q有限制條件q≠0，思路豁然開朗，方程（*）必有一根為0，代入得學生經歷了困惑、領悟的過程，加深了對概念的理解.

例4已知數列｛an｝中，a2=1，前n項和為Sn，且Sn=

（1）求a1.

（2）證明數列｛an｝為等差數列，并寫出其通項公式.

（3）設lgbn=試問是否存在正整數p，q（其中1

解題分析：令n=1，容易得a1=0.

（n-1）an+1=nan，（1）

學生因an+1-an不能得到是常數而思路中斷.學生中斷思路原因是判定等差數列方法單一，師生共同分析努力走出困境.

思路一：從等差中項來判斷：對（1）式遞推得nan+2=（n+1）an+1.（2）

兩相加得，得nan+2+nan=2nan+1，即an+2+an=2an+1.

如何尋找滿足條件的（p，q），學生不知道如何處理.當我們遇到一個比較復雜的問題時，不妨退到最簡單的情況，通過簡單情況的研究逐步推廣到復雜情況.當p=2時得q=3；當p=3時，等式顯然不成立.依次類推當p≥3，且p∈N*時數列為遞減數列，于是所以此時方程（☆）無正整數解.易知（p，q）=（2，3）

解題啟示：學生思維受阻可能是知識理解上存在偏差，如等差數列判斷與證明有多種方法，當定義失效，能否通過二階遞推回到等差中項來判斷，能否求出通項公式來判斷；也有可能是思維方法上缺失，如第（3）小題，通過特殊化研究，來尋求整體思路，在探索過程中獲得成就感和滿足感，一定能激發學生的學習興趣.

四、利用培養思維的思辯性

嘗試犯錯中發現辨別概念內涵、關注起始條件對解題的重要意義，培養與積累關注細節、綜合分析的能力.

分析粗疏、思維單向是學生在數學解題過程中常有的問題，靠正面提醒或強調往往效果不明顯，這次糾正，下次又會重犯.如果讓學生在自主嘗試中犯錯，又讓學生在自我分析或討論中明白錯誤原因，發現正確途徑，學生就會記住教訓，在辨別概念內涵、關注起始條件方面細心起來.

例5已知數列｛an｝和｛bn｝是等差數列，Sn，Tn分別是它們的前n項和，且求值.

例6已知數列｛an｝滿足（n≥2），若am=2014，則m=_______

解題分析：數列問題在遞推是要注意題目的起始條件，在上（1）式中n≥2，在（2）式中n≥1，故累乘知即又a1=a2=1，所以an=通過嘗試犯錯，學生對解題細節就會重視關注起來，逐步養成嚴密思維品質，確保解題無懈可擊.

如果學生在“多次發現”“多次教訓”中不斷關注概念內涵、不斷關注起始條件，從而獲得正確的解題途徑，學生的綜合解題能力就會發生飛躍.

古代教育家孔子曾說：“不憤不啟，不悱不發，舉一隅不以三隅反，則不復也.”意思是說：“不到學生努力想弄明白但仍然想不透的程度時先不要去開導他；不到學生心里明白卻又不能完善表達出來的程度時也不要去啟發他.如果他不能舉一反三，就不要再反復地給他們舉例了.”

意大利報人兼發行人朗根尼西也曾說過：“不要給我忠告，讓我自己去犯錯.”意思是說有些事情，只有自我實踐中有了教訓，才能逐漸成熟并獲得智慧.

這些思想，在高中數學教學中有著特別重要的意義.“嘗試—犯錯—發現—積累”的教學方法，是這種思想的最好實踐.