根深才能葉茂
——基于一類課本習題的探究

☉江蘇省宜興市第一中學 杜亞強

根深才能葉茂
——基于一類課本習題的探究

☉江蘇省宜興市第一中學 杜亞強

數學教學是培養學生運用所學知識解決實際問題的能力，在此過程中提高學生的思維水平，培養學生獨立分析問題、解決問題的能力.章建躍博士曾說過“課本是一科之本，課堂教學應‘以課本為本’”.的確，我們從事教學的主要工具——教材，里面有著取之不完、用之不盡的研究素材，筆者通過一類課本習題的研究性學習，取得了一些意想不到的結果，現把它寫出來，供共同商討、研究、學習之用.

一、問題的提出

蘇教版《普通高中課程標準實驗教科書·數學（選修2-1）》上有這樣的幾道習題：

習題1：已知直線y=x-2與拋物線y2=2x相交于點A，B，求證：OA⊥OB.

習題2：已知直線y=x+b與拋物線x2=2y交于A，B兩點，且OA⊥OB（O為坐標原點），求b的值（.該習題同時也出現在《選修1-1》P60上）

習題3：已知頂點為坐標原點，焦點在x軸正半軸上的拋物線有一個內接直角三角形，直角頂點在原點，斜邊長是一條直角邊所在直線的方程是y=2x，求拋物線的方程.

這三道習題，分別是課本54頁、67頁的習題，其都涉及這樣一個事實：過拋物線的頂點有兩條互相垂直的直線與拋物線相交于另外兩點.教材上為數不多的例題習題中，竟然有3道習題涉及同一個模型，應該引起教師學生的注意和重視.

章建躍博士說過：“課本是使學生學做人做事的基本載體，脫離課本的教學不是好的數學教學.”高考試題中有相當一部分試題是對“三基”的考查，雖然不大可能考查課本原題，但許多考題就是對課本原題的變形、改編或者是綜合，這些考題都能在課本上找到源頭.因此教學復習中，要重視課本，要重視例題習題的通性通法，適當對例題習題進行變式等，進一步落實基礎，以不變應萬變.

二、問題的探究

探究1：如圖1，已知拋物線C：y2=2px（p>0），過原點有兩條互相垂直的直線分別交拋物線于A，B兩點，試問直線AB有什么特點？

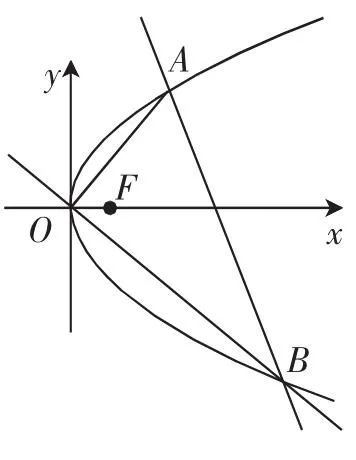
圖1

解析：記直線OA的方程為y= kx（k≠0），聯立方程消去y得到k2x2=2px，從而有A以代替k，可以得到B（2pk2，-2pk）.當k≠±1時，直線AB的斜率為所以直線AB的方程為即即即所以直線過點（2p，0）.當k=±1時，A，B兩點的橫坐標都是2p，直線AB也就過點（2p，0）了.所以直線AB恒過定點（2p，0）.

結論1：過拋物線y2=2px的頂點任意作兩條互相垂直的直線交拋物線于另外兩點A，B，則直線AB過定點（2p，0）.

探究2：如圖2，已知橢圓的左頂點為E，過E有兩條互相垂直的直線分別交橢圓于A，B兩點，試問直線AB有什么特點？

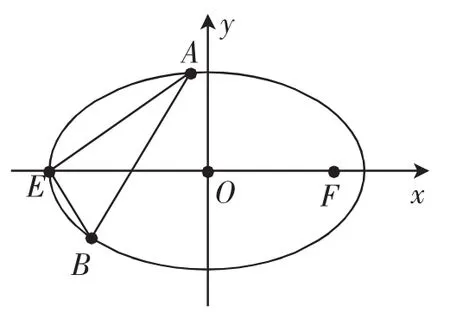
圖2

解析：記直線EA的方程為y=k（x+a）（k≠0），聯立方程消去y得到（a2k2+b2）x2+2a3k2x+a2（a2k2-b2）= 0，從而有A以代替k，可以得到B當k≠±1時，直線AB的斜率為所以直線AB的方程為即所以直線過點當k=±1時，A，B兩點的橫坐標都是直線AB也就過點了.所以直線AB恒過定點

結論2：過橢圓的左頂點任意作兩條互相垂直的直線交橢圓于另外兩點A，B，則直線AB過定點

探究3：如圖3，已知橢圓C的上頂點為E，過E有兩條互相垂直的直線分別交橢圓于A，B兩點，試問直線AB有什么特點？

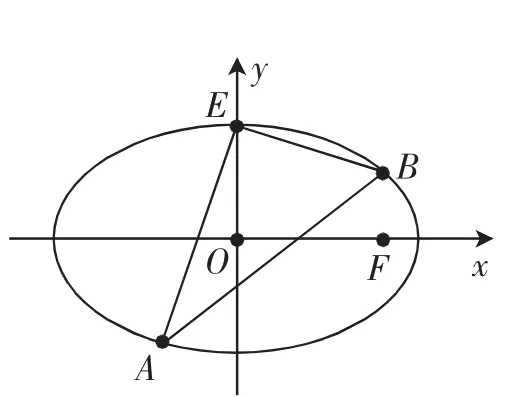
圖3

解析：與如上探究2的解析類似，可以得到直線AB恒過定點

結論3：過橢圓的上頂點任意作兩條互相垂直的直線交橢圓于另外兩點A，B，則直線AB過定點

探究4：如圖4，已知雙曲線C的右頂點為E，過E有兩條互相垂直的直線分別交雙曲線于另外兩點A，B，試問直線AB有什么特點？

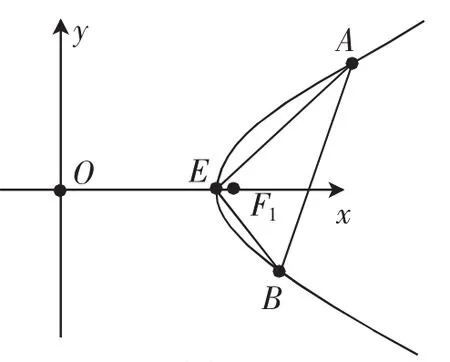
圖4

解析：（限于篇幅本文僅考慮a>b的情形，左半支圖形略）記直線EA的方程為y=k（x-a）（k≠0），聯立方程消去y得到（a2k2-b2）x2-2a3k2x+a2（a2k2+b2）=0，從而有A以代替k，可以得到當k≠±1時，直線AB的斜率為所以直線AB的方程為即所以直線過點當k=±1時，A，B兩點的橫坐標都是直線AB也就過點了.故直線AB恒過定點

結論4：過雙曲線的右頂點任意作兩條互相垂直的直線交雙曲線于另外兩點A，B，則直線AB過定點

三、結論的拓展

細究如上探究過程，可以發現，如上結論的逆命題也成立.

拓展1：給定拋物線y2=2px，過點（2p，0）任意作直線交拋物線于另外兩點A，B，則線段AB對頂點張直角.

拓展2：給定橢圓過點任意作直線交橢圓于另外兩點A，B，則線段AB對左頂點張直角.

拓展3：給定橢圓過點任意作直線交橢圓于另外兩點A，B，則線段AB對上頂點張直角.

拓展4：給定雙曲線過點任意作直線交雙曲線于另外兩點A，B，則線段AB對右頂點張直角.

顯然，由對稱性，還可以發現其他的定點和直角.

四、結論運用——考題鏈接

例1（2013年安徽理）已知直線y=a交拋物線y=x2于A，B兩點，若該拋物線上存在點C，使得∠ACB為直角，則a的取值范圍為__________.

解析：由結論1、拓展1及對稱性，可以發現，直線y=1交拋物線得到的A，B兩點對頂點張直角，點C在頂點處就滿足要求.由題意，只要直線y=1向上移動即可，所以a的取值范圍為a≥1.

例2（無錫市2015屆高三第一學期期末考試）如圖5，已知橢圓C：的上頂點為A，直線l：y=kx+ m交橢圓于P，Q兩點，設直線AP，AQ的斜率分別為k1，k2.

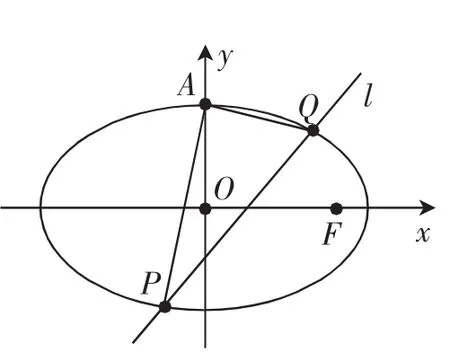
圖5

（1）略；

（2）若k1k2=-1時，證明：直線l：y=kx+m過定點.

解析：k1k2=-1就表示直線AP，AQ互相垂直，由結論3，直線l必過定點

例3如圖6，已知焦點在x軸上的橢圓C過點（0，1），且離心率為Q為橢圓C的左頂點.

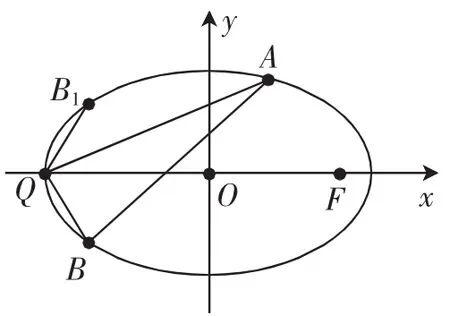
圖6

（1）求橢圓C的標準方程；

解析：（1）易得

學生在上述自主探究的過程中，不僅僅是完成一個個結論，更是寶貴的生命歷程，心智的參與過程，從而可使學生感知獲取知識的不易與艱難.整個探究過程中思維的調控、優化，不僅是能力的提高，更是對學習信心的激發.

五、教學反思

波利亞說：“一個專心的認真備課的老師能夠拿出一個有意義的但又不太復雜的題目，去幫助學生挖掘問題的各個方面，使得通過這道題，就像通過一道門戶，把學生引入一個完整的數學鄰域.”首先，學生的主觀能動性得到發揮.讓學生自己去研究問題，獲得對知識的再發現，這本身就是獲取知識的心路歷程，要讓學生知曉探究知識的過程是艱辛的，但是獲取知識的結果是一件令人興奮的事，同時也體現了對學生的教學不一定非要在課堂講授，也可以是課外，教學和研究是相輔相成的，雙方是充滿互動的.教師在教學中可以在這方面多研究，多下功夫，這對學生的成長歷程都是有幫助的.正如日本數學教育家米山國藏所說：“學生在學校所學的數學知識，畢業后若沒什么機會去用，一兩年后就會忘掉.然而，不管他從事什么工作，唯有深深銘刻在心中的數學的精神，數學的思維方法，研究方法，推理方法和看問題的著眼點等，卻隨時隨地的發生作用，使他們受益終生.”通過研究性學習，使筆者深深意識到除做好日常教學外，可以多開展這樣的研究性學習，使學生學中樂，樂中學，真正做到教學相長.

我們一線數學教師備課時要善于思考，善于聯系，特別是課本上的習題，題目雖小，往往藏有大乾坤，通過教師的講解，為學生做好知識鋪墊，順理成章地引導學生，使之達到會一題、通一類的目的，同時，也水到渠成地提升了教師本身的專業素養.