思維深度決定視覺寬度

☉江蘇省高淳高級中學 田丕豐

思維深度決定視覺寬度

☉江蘇省高淳高級中學 田丕豐

（1）求a，b的值；

（2）用x1表示x2；

（3）求證：點M在定直線l上.

這題是我校2015屆高三考前適應性考試的試題，問第（1）問是對有關基礎知識的考查，除個別學生外，都能很快得到正確的結果：a=2，b=1，＋y2＝1.第（2）問的設計意圖是為解答問第（3）問指明思維方向，降低求解難度.考試后統計表明，能解答第（2）問的學生中，大多數都能完成第（3）問的求解.因此，能否解答第（2）問，是能否完整解答此題的關鍵點.筆者在閱卷中發現學生對第（2）問求解，出現了四種解法，下面輯錄的是這幾種解法和筆者的一些淺顯的思考.

【解法一】（2）（i）若直線斜率存在時，設直線方程y＝k（x-1），

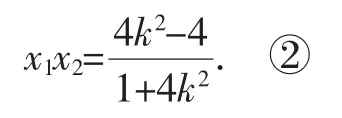
將此式子代入①，化簡得5（x1＋x2）-2x1x2＝8，

（ii）若斜率不存在時，x1＝x2＝1，滿足上式.

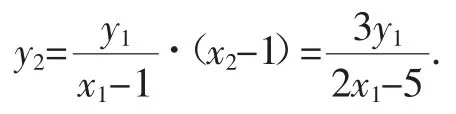
因此，點M在定直線：x=4上.

【評析1】這一解法注意到決定題中各個動點位置的控制變量是直線PQ的斜率k，利用k找到相關動點坐標之間的關系，在本題的設問方式下，學生容易想到消去實數k找出x1，x2的關系，在此基礎上解答第（3）問較為順利.因此，對本題來說，這一解法的思維雖然淺顯，卻直觀有效.但若本題中沒有設置第（2）問，用此法時，因為中間目標的缺失，一般學生的思路是用k表示點M的坐標，這樣面對很復雜、煩瑣的代數式運算，從而導致解題過程無法推進.

以下各種解法，只給出第（2）問的求解過程，第（3）問的解法與上面大致相同，所以省略.

【解法二】設P（x1，y1），Q（x2，y2），M（x0，y0）.若x1≠1，直線PQ方程為代入橢圓方程消去y，得［（x1-1）2＋4y21］x2-8y21x＋4y21-4（x1-1）2＝0，且x21＋4y21＝4，所以（5-2x1）x2-8y21x-5x21＋8x1＝0.由韋達定理得

【評析2】此解法是思考到問題能否獲解的關鍵是設法表示出各個動點的坐標，因而選擇動點P的橫坐標作為控制變量，直接通過求解方程得到x2與x1的關系，比解法一減少了消參的環節.因此，用此法的學生要比用解法一的學生思維更深一些，而且此法對于在已知曲線聯動的兩個動點的題型，具有普遍的指導意義.需要提醒的是解題過程中，利用韋達定理可以簡化運算.但此法只有學科基礎較好、感悟能力較強的學生，經過對相關題型的批量訓練才能掌握.

【評析3】此法是利用定比分點的向量形式，找到了關聯動點相應坐標的線性關系，再用點差法得動點坐標與參數λ的線性關系，這樣消參就很順利.應該說能想到此法的學生，思維層次較高，綜合應用學科知識的意識與能力較好.而且，此法用于處理過定點的動線段兩端點相應坐標之間的關系，通常是一種行之有效，運算也不煩瑣的好方法.

【解法四】由題知，P（x1，y1），Q（x2，y2），T（1，0），由P，Q，T三點共線得：KPT＝KQT，所以即y（21x2-1）2＝y22（x1-1）2.又有

代入上式得（4-x21）（x2-1）2＝（4-x22）（x1-1）2，

即4（x2-1）2-4（x1-1）2＝x21（x2-1）2-x22（x1-1）2.

由平方差公式整理得5（x1＋x2）-2x1x2＝8，所以x2＝

【評析4】此解法是從多元方程組中通過消元得到部分未知數之間的關系，是實質是從關聯動點的運動與變化中，找到相關變量的不變關系.用此法的學生對二次曲線方程的結構特征有較深的研究，能夠洞察方程間各類運算的可能結果，對本題中各個條件的代數表示及應用有自己獨特的視角，思維廣度與深度明顯高人一等.不過，此法因其獨特，言傳效果不佳，只適合于一些有學科特質的學生理解與掌握.

【后記】我們知道：運動與變化、控與被控是解析幾何中所蘊涵的最重要的思想方法，而解決這兩個問題最基本的數學工具是方程與不等式，因此，數式運算能力的培養是提高解析幾何解題能力的基礎.上題中幾種解法體現，學生解題時的思維深度，決定其解題的視角寬度，也決定了方法的優劣與運算的繁簡程度.就教學價值而言，筆者認為前兩種解法優于后兩種解法.因此，實際教學時，應通過思路分析和解題訓練，幫助學生理解和掌握前兩種方法.解法一因其思維起點低、入口寬，學生易于理解，是培養學生思維能力必不可少的奠基石.雖然在后續的求解過程中，學生可能因思維偏差和運算能力的欠缺導致解題受挫，同時由于學生有簡化運算的心理需求，利于激發學生思維橫向拓展和縱向深入的內驅力，優化學生的思維品質.解法二，因其對解題過程相對深入和全方位的思考，且方法具有普遍性指導意義，更具集體教學價值.后兩種解法，雖然思維層次很高，但思維切入點隱而難求，且方法的遷移性不強，因而不適合進行以班級為單位的集體教學，可針對部分學科基礎好、思維能力強的學生，預先準備好相關題組，在教師指導下自主探究，或許可以取得較好的效果.這是筆者對上題各種解法的一點淺顯的思考，不知當否？錄此，以博方家一哂.