基于Markov模型麻醉機生產(chǎn)線相鄰工位最佳看板數(shù)量研究
王燕茹 王凱凱
江南大學(xué)商學(xué)院
基于Markov模型麻醉機生產(chǎn)線相鄰工位最佳看板數(shù)量研究
王燕茹 王凱凱
江南大學(xué)商學(xué)院
利用馬爾科夫(Markov)模型求解單級生產(chǎn)系統(tǒng)相鄰工位之間的最佳看板,并依據(jù)生產(chǎn)過程中最小總期望成本來約束使用的看板數(shù)量。通過確定最佳看板數(shù)量,目的是為了促使生產(chǎn)過程按照看板數(shù)量有序生產(chǎn),減少生產(chǎn)過程中不必要的成本浪費。文中證明馬爾科夫模型在確定生產(chǎn)看板數(shù)量方面有良好的學(xué)術(shù)效果和實踐意義。
馬爾科夫模型 相鄰工位 總期望成本
一、緒論
(一)研究的意義
看板管理,是指為了達到JIT準時生產(chǎn)方式而嚴格控制生產(chǎn)流程的工具。看板是一種工廠內(nèi)部推動生產(chǎn)運作的信息流。針對于工廠內(nèi)部物料流而言,工廠內(nèi)部的物料流是指工廠內(nèi)部用于生產(chǎn)從倉儲配料至生產(chǎn)到完成客戶最終需求產(chǎn)品的整個物料流動過程。物料流和信息流是相輔相成的兩個過程。
但是基于看板管理的生產(chǎn)過程中,信息流與物料流的流動方向正好相反,它是建立在生產(chǎn)物料流的前提下,逆向從最末道工序開始向前拉動一步步直到開始端,進而推動完成物料在工廠里流動的全過程。因而整個循環(huán)過程,就是看板系統(tǒng)的運作過程。確定看板卡最佳使用數(shù)量,通過求得生產(chǎn)過程中消耗的總成本,對于降低生產(chǎn)過程中不必要的成本費用具有重要意義。
(二)國內(nèi)外研究動態(tài)
關(guān)于最佳看板數(shù)量的研究,國內(nèi)外專家學(xué)者都有相關(guān)方面的文獻。比如,國內(nèi)學(xué)者林勇、樂曉娟等(2006年)引用CONWIP混合生產(chǎn)控制方法通過生產(chǎn)線看板總數(shù)調(diào)節(jié)在制品總量。
國外一些學(xué)者如Rees(1987)提出一套流程,目的是為能夠在相對不穩(wěn)定的環(huán)境下動態(tài)地調(diào)整生產(chǎn)過程中的看板數(shù)量;Bitran和Chang(1987)研究出一種應(yīng)用于確定的、多級的、具有裝配樹結(jié)構(gòu)的生產(chǎn)環(huán)境的一種看板系統(tǒng)的數(shù)學(xué)模型;Askin(1993)提出一種求解最佳看板的隨機模型,應(yīng)用于同時生產(chǎn)多產(chǎn)品類型的生產(chǎn)線中;Karmarkar和Kekre(1989)使用不同的單—雙看板研究生產(chǎn)提前期的批次效果;Pan和Liao(1989),Yilmaz(1992)研究出一種應(yīng)用于兩級生產(chǎn)系統(tǒng)中關(guān)于最佳的訂單和生產(chǎn)數(shù)量模型;Siha(1994)使用時間連續(xù)的馬爾科夫鏈為拉式生產(chǎn)建立數(shù)學(xué)模型。
二、相關(guān)理論基礎(chǔ)
假定工位A和工位B是處于N級生產(chǎn)線中間連續(xù)相鄰的操作工位,且生產(chǎn)線的物料流是從A向B。最初,B從A獲取生產(chǎn)所需的原物料,A會將B所需物料通過看板周轉(zhuǎn)箱的方式傳送給B,待產(chǎn)品組裝完成時,A發(fā)送配料請求給前一工位申請分配所需物料,B會通過回執(zhí)空周轉(zhuǎn)箱給A,發(fā)送物料領(lǐng)取要求。A得到指令后傳送給B來執(zhí)行此請求。
將排隊理論應(yīng)用在生產(chǎn)線中,對于看板系統(tǒng)的工位A,假定物料以固定的生產(chǎn)節(jié)拍在A進行生產(chǎn)然后以固定的需求節(jié)拍傳送給B。且在拉式生產(chǎn)中,A傳送物料只能按照B的需求節(jié)拍傳送。因此,在生產(chǎn)線B的需求節(jié)拍等同于排隊理論的服務(wù)節(jié)拍。類似地,生產(chǎn)節(jié)拍等同于顧客到達節(jié)拍。
在建立數(shù)學(xué)模型之前需要對相關(guān)的參數(shù)進行假設(shè):
三、建立模型及分析
(一)建立馬爾科夫數(shù)學(xué)模型

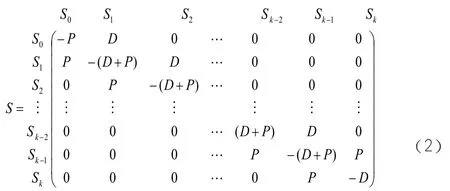



(5)
(二)看板系統(tǒng)總期望成本
為了求得最佳看板使用數(shù)量,通過計算看板系統(tǒng)中總期望成本的最小值。總期望成本主要由兩部分組成:一部分是缺料成本另一部分是維持成本,用表示。因此,總期望成本寫成如下表達式:

首先,假設(shè)相鄰兩個工位A和B之間只是存在一個看板在流通,那么只會存在兩種狀態(tài)轉(zhuǎn)移的情況。所以這種情況下的看板系統(tǒng)的轉(zhuǎn)移矩陣可以寫成如下形式:

那么對應(yīng)的馬爾科夫差分方程的系數(shù)矩陣應(yīng)該是

因此,相鄰工位只有一個看板流通的系統(tǒng)的定態(tài)方程式,可以根據(jù)(5)(8)求得的值。


同理,如果在相鄰兩個工位之間存在兩個看板進行流通,那么這兩個周轉(zhuǎn)箱會存在三種狀態(tài),在一個中間階段以此類推,矩陣和可以寫成以下:
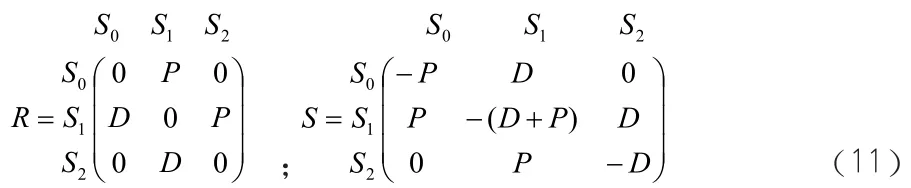
所以含有兩個看板流通的系統(tǒng)的定態(tài)等式可得:
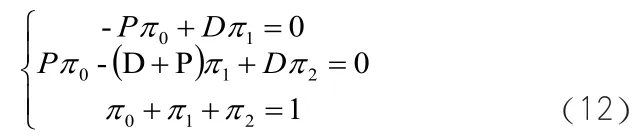


由以上三種不同看板數(shù)量的總期望成本表達式可以歸納,總期望成本會服從某一規(guī)律。根據(jù)歸納法,當(dāng)相鄰兩工位之間存在個看板流通時可以寫成如下表達式




然后將這三個公式代入(18)(19)并簡化,得到以下不等式:

四、實例求證
在本小節(jié)中,將上述所建立的數(shù)學(xué)模型應(yīng)用到麻醉機生產(chǎn)線中,根據(jù)麻醉機生產(chǎn)線中各個工位的實際生產(chǎn)節(jié)拍和需求節(jié)拍缺料造成的損失成本以及看板周轉(zhuǎn)箱的維持成本等得到的真實數(shù)據(jù),求解生產(chǎn)線的最佳看板。
根據(jù)實際統(tǒng)計數(shù)據(jù),麻醉機生產(chǎn)線的工藝流程基本要經(jīng)過多次組裝、機架裝配、電氣功能測試、高壓低壓測試、最終裝配、機器包裝等工藝流程。如下圖1所示:

圖1 麻醉機生產(chǎn)線基本工藝流程圖
根據(jù)生產(chǎn)線的實際要求,經(jīng)過多次反復(fù)測試和平均時間計算,參數(shù)生產(chǎn)節(jié)拍(生產(chǎn)一套所需時間)、需求節(jié)拍(需求一套所需時間)、缺料成本(生產(chǎn)缺料損失)以及周轉(zhuǎn)箱維持成本基本參數(shù)如下:

那么根據(jù)實際提供的參數(shù),可以計算相鄰工位之間的最佳看板數(shù)量依據(jù)之前因此代入?yún)?shù)求得總期望成本如下:

并將參數(shù)代入(23)兩個不等式中得

五、結(jié)論
利用馬爾科夫(Markov)模型簡單、初步地求解生產(chǎn)看板中的最優(yōu)過程,通過使生產(chǎn)過程中總期望成本最小化來獲得最佳看板數(shù)量。文章中以二級系統(tǒng)為例,考慮生產(chǎn)線中只有兩個裝配工位的過程,并對相關(guān)參數(shù)進行實際調(diào)查和統(tǒng)計,以及某些參數(shù)由于影響因素較小而忽略不計。但是,實際的生產(chǎn)過程中考慮參數(shù)更多,裝配工位更加復(fù)雜,因此對以后將該模型擴展到更加復(fù)雜的影響因子、多級系統(tǒng)的生產(chǎn)流程中提供基礎(chǔ)理論和參考依據(jù)。
[1]林勇,樂曉娟,付秋芳.Push/Pull和CONWIP/Pull生產(chǎn)控制模式對比分析 [J].工業(yè)工程,2006,9(2):6-10.
[2]Rees,L.P., Philipoom,P.R., Taylor, B.W.I, and Huang, P.Y., Dynamically adjusting the number of Kanbans in a Just-in-time production system using estimated values in leadtime [J].IIE Transitions,1987,19,199-207.
[3]Bitran, G.R., and Chang,L., A mathematical programming approach to a dererministic Kanban system [J].Management science,1987,33,427-441.
[4]Askin,R.G.,Miteasi,M.G.,and Golderc,J.B., Determining the number of Kanbans in multi-item Just-in-time systems [J].IIE Transitions,1993,25,89-98.
[5]Karmarkar,U.S.,and Teyre,S., Batching policy in Kanban systems [J].Journal of Manufaturing systems,1989,8,317-328.
[6]Pan,A.C., and Liao,C.J., An inventory model under Justin-time purchasing agreements, [J].Production and Inventory Management,1989,30,49-52.
[7]Siha,S., The pull production system:modelling and characteristics,[J].International Journal of Production Research,1994,32,933-949.
[8]VIJAY S. NORI, BHABA R SARKER. Optimum numBer of Kanbans Between two adjacent stations [J]. Production Planning&Control,1998,9(1):60-65.
王燕茹(1960.12-),女,內(nèi)蒙古呼和浩特人,副教授,碩士生導(dǎo)師,主要研究領(lǐng)域:營銷管理、旅游管理等;王凱凱(1991.11-),男,山東省濰坊市人,碩士研究生,主要研究方向:生產(chǎn)企業(yè)物流的管理與運作。
中央高校基本科研業(yè)務(wù)費專項資金資助項目(JUSRP1601XNC)。

