數形結合

李進衛

【摘要】生活中一些事物的數量，有時不用精確的數表示，而只用一個與它比較接近的數來表示，這樣的數是近似數，計量的精確度系指測得值與真實值之間的接近程度。小學五年級學生在學習“求小數的近似數”時有兩個難點：一是如何讓學生理解保留到整數，要看十分位，保留一位小數，要看百分位，……；二是將一個小數保留兩位小數得到了1.50后，為什么末尾的0不能去掉，1.50比1.5更精確。

【關鍵詞】近似數 數軸 精確度 數形結合

我們知道，“生活中一些事物的數量，有時不用精確的數表示，而只用一個與它比較接近的數來表示，這樣的數是近似數”。小學生在學習“求小數的近似數”時會遇到兩個難點：一是如何讓學生理解保留到整數，要看十分位，并和5比，保留一位小數，要看百分位，并和5比……二是將一個小數保留兩位小數得到了1.50后，為什么1.50比1.5更精確？學生出現這些認知難點原因是什么，教學中如何突破難點呢？

一、產生認知難點的原因分析

首先是新舊知識聯系松散。小學階段關于近似數知識的安排有的是顯性的，以例題形式出現；有的是隱性的，以習題形式出現。學生學習經歷了幾個階段：先是在低年級初步感知近似數的相關知識，如32更接近30還是40？在后面學習除數是兩位數的除法時，學生會將除數看作一個整十數，實際上就是使用了近似數的知識。把一個整數用“萬”或“億”作單位寫出它的近似數，最后學習求小數的近似數。小數的近似數知識雖和整數的近似數知識方法差不多，可是在學習求小數的近似數之前，學生已經很長時間沒有接觸近似數的相關知識，已有的知識差不多遺忘，所以不能指望近似數知識的原理在新的情境中自然遷移。

其次，沒有深刻理解整數的近似數知識。學生學習整數的近似數知識雖經歷了探索的過程，但對學生進行學情調查后發現，學生解答相關習題的技能還在，對于四舍五入到萬位，要和千位上的“5”比較的道理說不清。顯然關于近似數知識中的道理理解不深刻，原有的記憶無法提取和應用。

二、教學中如何突破難點

《義務教育數學課程標準》（2011年版）明確提出：“幾何直觀主要是指利用圖形描述和分析問題。借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。”徐文彬指出：“其實，這里有三層含義。首先是以形助數，形象、直觀地實現由數至形的轉化與表達；其次是在以形助數的基礎上，促使以形解數的完成；第三是在以形助數和以形解數的基礎上，幫助學生形成數形結合之數學直觀能力。即把數量關系和空間形式結合起來去分析問題、解決問題，也就是數形結合思想。”根據學生認知特點，采用數形結合，是理解小數近似數知識的最佳路徑。

1.借助數軸，理解和“5”比的道理

（1）保留到整數，為什么與十分位的5比

蘇教版教材中原來的例題是：“地球和太陽之間的平均距離大約是1.496億千米。精確到十分位是多少億千米？精確到百分位是多少億千米？”例題直接從保留一位小數入手，缺少了保留到整數經驗，與學生原有掌握的知識跨度大，造成學生理解困難。實際教學可以增加一個問題：“精確到個位是多少億千米？”從保留到整數入手，突破難點。

根據原有的知識，學生知道1.496比1大，比2小。保留到整數只可能等于1或2。教師畫出數軸，將1和2之間的線段平均分成10份。

提問學生，要看1.496等于幾應該和誰比呢？學生通過看圖知道應該和中間數1.5比。1.496在1.5的左邊，更接近于1，因此1.496≈1。

教學到這里，學生還沒有理解保留到整數要和十分位上的5比較的道理。這時通過板書，將1.496和1.5比較。提問學生如果不畫圖將1.496保留到整數，應該怎樣想呢？學生知道應該將1.496和1.5比。兩數比較時，學生發現1.496和1.5的整數部分相同，十分位后面的數對于最后的結果沒有影響，因此只要看十分位就可以了，即只要和十分位的5比就可以了。如果大于或等于5就約等于2，如果小于5就約等于1。

在這里適時出示一組習題：將1.89、2.146、8.575、6.4287保留到整數應該和誰比？學生知道這幾個數分別和1.5、2.5、8.5、6.5相比。通過板書進行比較后發現，每一組數中的整數部分都是相同的，十分位都是5，十分位后面的數對于最后的結果沒有影響，因此只要把十分位上的數與5比較就可以了。通過數形結合，學生明白了將一個小數保留到整數只要和十分位上的5比，如果十分位上的數比5大就向個位進1，如果比5小，就全部舍去。

（2）保留到十分位，自主探索求近似數的方法

學生理解了將一個小數保留到整數只要看十分位，并且和5比的道理后，接下來教學將一個小數保留一位小數時，可以根據幾個問題采取自主探索的形式。問題是：將1.496保留一位小數可能得到哪些結果？1.496和哪個數比較呢？將1.496保留一位小數的方法是什么？

學生通過自主探索，知道將1.496保留一位小數只可能得到1.4和1.5這兩種結果。應該和1.45比較。教師根據學生探索出的結果，運用數軸讓學生直觀觀察。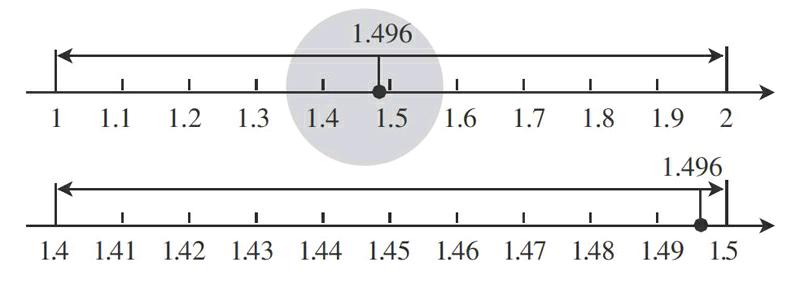

如上圖，教師將第一幅圖中1.4和1.5之間的一段放大，將這一段也平均分成10份，得到第二幅圖。學生通過看圖清楚地知道，1.496大于1.4小于1.5，因此保留一位小數可能是1.4或者1.5。從圖上看，1.4和1.5之間的中間數是1.45。1.496比1.45大的多，所以1.496≈1.5。

教師同樣出示題目：將7.54、0.365、0.295保留一位小數，分別和誰比？學生知道分別和7.55、0.35、0.25比。通過比較發現，每一組數的整數部分、十分位都相同，只要看百分位并和5比即可。百分位后面的部分對最后的結果沒有影響，忽略不計。 通過數形結合，學生明白了將一個小數保留一位小數只要和百分位上的5比，比5大就向十分位進1，比5小就全部舍去。

接下來教學將一個小數保留兩位小數時，學生可以嘗試練習，練習后教師同樣運用數軸講清道理。

如上圖，教師將第二幅圖中1.49和1.50之間的一段放大，將這一段也平均分成10份，1.496比1.49大，比1.50小。將1.496保留兩位小數結果只可能得到1.49或1.50，1.49和1.50之間的中間數是1.495。1.496比1.495大，所以1.496≈1.50。

2.借助數軸，深刻理解精確度

將1.496保留兩位小數時，學生會出現1.50和1.5兩種結果。怎樣讓學生理解1.50比1.5更精確呢？

如圖所示，將1.496保留一位小數，我們要看1.4到1.5這之間的數；將1.496保留兩位小數，觀察的是1.49到1.50之間的數。反過來想，如果一個小數保留一位小數后是1.5，那么這個小數可能是1.45和1.5之間的任何一個數；保留兩位小數后是1.50，那么這個小數可能是1.495和1.50之間的任何一個數。這兩個區間中的數分別與1.5及1.50的差是不一樣的，從圖上可以清晰地看出1.495和1.50之間的數與1.50的差更小，即1.50更精確。

“數量關系獲得幾何解釋，可以使問題變得直觀形象，使人易于洞察問題的本質；幾何問題得到代數表示，可以使抽象的推理論證轉化為程序化操作的代數運算，實現化難為易的目的。代數給人以精確，幾何給人以直觀，當這兩門學科結合成伴侶時，它們就相互吸取新鮮活力，以最快的速度走向完善。”小學數學教學中應該將一些復雜的問題直觀化，使問題變得直觀、形象、易于觀察。“數與形之間的關系，貌似無關，如果能從中發現它們之間共同的關鍵特征，就能獲得一種對知識的全新理解。

【參考文獻】

[1]中華人民共和國教育部.義務教育數學課程標準（2011版）[S].北京：北京師范大學出版社，2012.

[2]徐文彬.數學結合思想的歷史發展、思維意蘊與教學價值[J].小學數學教育，2015（5）.

[3]曹才翰，章建躍.數學教育心理學[M].北京：北京師范大學出版社，2002.