巧用單位圓解決三角函數(shù)問題的思考

王宏偉

（甘肅省慶陽市第二中學(xué)）

巧用單位圓解決三角函數(shù)問題的思考

王宏偉

（甘肅省慶陽市第二中學(xué)）

在高中數(shù)學(xué)教學(xué)階段，單位圓是應(yīng)用較為廣泛的一種解題策略，尤其是在與三角函數(shù)相關(guān)的題目類型當中，其所能發(fā)揮的解題作用尤為明顯，將就“利用單位圓解決三角函數(shù)問題”展開討論。

三角函數(shù)問題;單位圓;解題技巧

單位圓上的三角函數(shù)線是實現(xiàn)數(shù)形結(jié)合的一種有效方式，是能夠?qū)θ呛瘮?shù)進行幾何表示的一種方法。很多學(xué)生在進行三角函數(shù)這一章節(jié)的學(xué)習(xí)時，會將學(xué)習(xí)的重點置于公式記憶、函數(shù)性質(zhì)的掌握以及圖像性質(zhì)的理解，對于單位圓三角函數(shù)線的部分卻掌握的不夠牢固。本文中筆者就將從以下幾個角度來著手探討這一類型問題的具體解題思路。

一、利用單位圓的三角函數(shù)線比較函數(shù)值大小

利用單位圓的三角函數(shù)線來比較函數(shù)值的大小，其解題關(guān)鍵就在于對三角函數(shù)、角等相關(guān)數(shù)學(xué)量的轉(zhuǎn)化過程，以這樣一道題目為例：

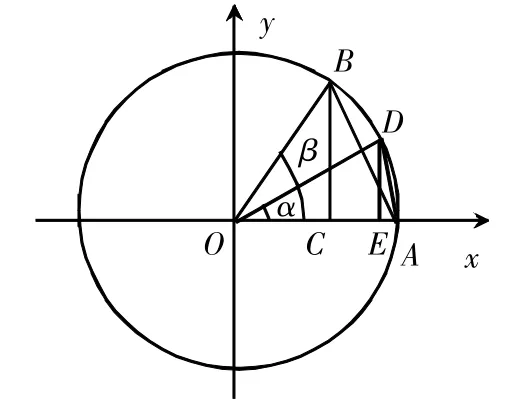
本題解題的難點在于sinα屬于三角函數(shù)值，但是α本身屬于角，二者之間屬于不同的領(lǐng)域，看似無法做尋常的加減運算，所以如果單純地想依靠計算的方式來進行判斷，顯然會陷入求解的瓶頸當中。

但是如果將題目當中所涉及的sinα、α等置于單位圓當中，我們發(fā)現(xiàn)，其本身在圖形領(lǐng)域所富含的另外一層含義，我們可以利用單位圓將所要比較大小的部分轉(zhuǎn)化為其他的、可以量化和具象化的內(nèi)容。……