“三位數的連續退位減法”教學研究報告

文︳長沙市岳麓區第一小學數學組瀟湘數學教育工作室

“三位數的連續退位減法”教學研究報告

文︳長沙市岳麓區第一小學數學組瀟湘數學教育工作室

一、問題

人教版三年級上冊第四單元“三位數的連續退位減法”是學生在學習了兩位數減兩位數的退位減法和整百、整十的三位數減三位數的減法的基礎上進一步學習的內容，同時它也是減法教學的節點。通讀教材，把握教學要求，我們認為這節課的教學目標是：不但要求學生從兩位數減法的經驗出發學習三位數的減法，而且要求學生掌握減法計算的通法，進行多位數的減法計算。從教材編排上看，三位數的減法只是將原有的兩位數改成三位數而已，看似非常簡單的一個內容，學生在計算時卻頻繁出錯，這種情況一直困擾著眾多教師。是什么原因使得學生在計算中頻繁出錯呢？我們又該如何幫助學生解決計算中遇到的問題，切實提高計算技能呢？為此，我們數學組針對這一內容進行了一些思考與實踐。

1.教學實踐中的問題與原因分析

為了切實掌握學生的學習起點，以及在計算中存在的問題，我們從三年級學生中隨機抽取了64名學生進行了教學前測，以下是前測的結果統計表。

題次題目計算正確粗心忘記退位①435-322 98.4% 1.6%②654-128 78.1% 9.4% 7.8% 4.7%③435-86 68.8% 6.3% 20.2% 4.7%④403-158 40.6% 1.6% 43.8% 14%計算錯誤會算理，計算錯誤不會算理，計算錯誤

從調查統計結果來看，學生在未學習這一內容時，三位數不退位的減法計算正確率是98.4%，然而在三位數退一位的減法計算時，正確率下降到78.1%，特別是被減數中間有0的連續退位減法計算，正確率僅為40.6%。通過對學生的問卷進行分析，我們發現學生主要存在以下兩個問題。

（1）學生忘記退位。

計算435－86時，個位上的5不夠減，需要向十位上的3借1當作10，與個位上的5合成15，再減6，個位上得9。計算十位時，十位上的3被個位上的5借去了1，十位上的3先減1，剩下2，2不夠減時，又要向百位上的4借1當作10，和十位上的2合成12，再減8，十位上得4。百位上的4被十位借去了1，百位上是3，所以得數是349。在計算435－86=349的過程中，十位的計算最復雜，經歷了減1（被個位上的5借去1），在十位上加10（向百位借1）的復雜過程。學生在計算的過程中很容易忘記十位上的3被個位上的5借去1，十位上沒有先減1就直接計算，于是出現了如圖1所示的忘記退位的情況。

圖1

在計算連續退位減法時，學生忘記退位的根本原因是：十位上的退位思維程序復雜，而且這種思維程序均不能直觀地表示出來，除了用退位點表示后一位借走的1，其他思維過程都需要在大腦中記憶。尤其是看到十位上帶有借位點的3在心里卻要當作2才行，這種“表里不一”的現象使得學生在計算的過程中很難做到知行合一，因而容易出錯。

（2）錯誤定義“跨位借”。

計算403－158時，個位上的3不夠減，需要向十位借1，而十位恰好是0時，學生很容易出現錯誤。計算個位時，學生認為十位上的0表示一個也沒有，個位無法向十位借到1，于是索性向百位上的4借1。借得百位上的1又恰與二年級“借1當10”的經驗相吻合，學生于是將百位上借得的1與個位上原有的3合成13，再減8，個位上得5。計算十位時，十位上是0，也不夠減，十位上的0也向百位上的4借1，十位上的0與百位上借得的1合成10，再減5，十位上得5。百位上的4被個位和十位都借去了1，所以百位上只剩下2，再減1，百位上得1。這樣一來，學生在計算時出現了如圖2所示的“跨位借”情況。

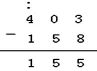
圖2

學生出現“跨位借”的主要原因是：學生不僅不知道如何處理這類十位上是0的情況，還受到二年級已經有的“借位”和“借1當10”經驗的影響，并不知道“借1當10”的意義。“借1當10”指的是個位不夠減時，向十位借得1，就在個位上加10；當十位不夠減時，十位向百位借得1，就在十位上加10。而并非這類學生所想的，個位跨過十位直接向百位借得的1，在個位上也只當作10，卻不知道百位上的1表示10個十或是100個一。正是因為二年級“借1當10”經驗的負遷移，學生才出現了這類“跨位借”的錯誤。

2.教學對策

通過以上分析，我們不僅了解了學生的學習基礎，還掌握了學生在學習中存在的問題。因此，在本節課的教學時，應注意以下幾個問題——

（1）在學生已有的兩位數減法計算經驗基礎上進行三位數的減法學習。

在學習本節內容之前，學生學習了兩位數減兩位數的退位減法以及整百、整十的三位數減三位數的減法，能熟練地列豎式計算，有了退位減法計算及“借1當10”的經驗。因此，在學習本節內容時，教師應當從學生已有的經驗出發，遷移學習三位數的減法，這樣既可以降低本節教學內容的難度，又能夠溝通三位數減法與兩位數減法之間的聯系，讓學生進一步理解減法計算之間的通性，也為后續學習多位數的減法打好鋪墊。

（2）總結口訣，提醒學生不要忘記退位。

為了解決學生在計算連續退位減法時總是忘記退位而頻繁出錯的問題，實際教學中，教師可以讓學生經歷連續退位減法的計算過程，獲得在計算中因忘記退位導致計算錯誤的教訓；接著，教師適時創編口訣“頭上有點就減1”，提醒學生在計算過程中看到退位點就要退位，從而提高計算的正確率。

（3）借助直觀形象的演示，幫助學生理解“借1當10”的意義，避免出現“跨位借”的現象。

學生有“借1當10”的經驗但并不理解“借1當10”的意義。學生在計算被減數十位上是0的三位數減法時，讓個位跨過十位向百位借1，并對“借1當10”進行草率的推廣，從而出現了“跨位借”的情況。教師直觀形象地演示個位如何向十位上的0借1的過程，能夠讓學生弄清楚“借1當10”的意義，避免在計算中出現“跨位借”的情況。

按照以上思路，我們進行了如下的教學嘗試。

二、實踐

1.遷移兩位數減兩位數的經驗，嘗試三位數的減法計算。

師：今天我們一起來學習筆算減法。之前我們學習了兩位數的筆算減法，考考你們，看你們掌握得怎么樣。（板書：435－18=）請同學們動手算一算，并思考，列豎式要注意什么？該如何進行計算？

生：列豎式時相同數位要對齊，從個位算起。

（學生獨立完成計算）

師：很多同學已經完成了計算，我們一起來計算。首先計算個位，個位上是5減8，不夠減，怎么辦呢？

生1：向前一位借1。

師：個位向誰借1呢？

生1：個位向十位借1。

師：在減法豎式計算時，不夠減向前一位借，為了便于記憶，我們通常使用借位點，表示個位向十位借了1。那個位向十位借得的1，在個位上表示多少個一呢？

生2：個位向十位借得的1，在個位上表示10個一。

師：個位向十位借得了10個一之后，個位上是多少呢？是怎么得到的？

生3：個位上是15，因為個位上原有5個一，又向十位借得了10個一，就合成了15個一。

師：說得真好，個位上就是15-8=7，所以個位上的得數是7。算完個位再算十位，被減數的十位上是幾呢？

生4：十位上是2。

師：我就納悶了，被減數的十位上分明是3，怎么說成是2呢？

生5：因為個位向十位借走了1。

師：你是怎么知道的？

生5：十位上有借位點。

師：是的，剛才計算個位時，個位向十位上的3借了1，就要減1，十位上只剩下2。像這種情況，我們就說要退位1。（板書：退位）十位上是2減1等于1，十位上的得數是1。接下來算百位，百位上就是4，所以435－18=417。你做對了嗎？舉手示意一下。（學生全部舉手）

師：很好，像這樣，遇到不夠減時，需要向前一位借1，本位就需要退位的減法，看來你們都會計算了。

設計意圖：由于前測的調查結果表明學生在學習三位數的減法之前已經具備一定的學習基礎，完全有能力對三位數的退位減法進行探究；且教材中小精靈的提示語“怎樣列豎式？”是為了讓學生回顧豎式計算時相同數位要對齊，我們在教學這一內容時，對教材進行了調整，將教材編排的例題1計算435－322改為435－18，更有利于學生理解豎式計算時相同數位要對齊這一原則。

2.總結口訣“頭上有點就減1”，提醒學生記得退位。

師：剛才你們已經會計算三位數的退位減法，老師這里還有一個難度更大的計算，（板書：435－86=）你們還能像剛才那樣非常輕松地解決嗎？

學生獨立完成，教師展示學生忘記退位的典型錯誤：435－86=359。

師：你們和他的答案相同嗎？（大部分學生搖頭表示不一樣）我們也一起算一算，如果他計算錯誤，幫他找找錯誤的原因，好嗎？

師：列豎式要注意，相同數位對齊，從個位算起。個位上是5減6，不夠減，怎么辦呢？

生6：得向十位借1。十位上的1與個位上原來的5合成15，個位就是15－6=9，個位上的得數是9。

師：很好，再算十位，十位上又怎么算？

生7：十位是2，2減8不夠減，得向百位借1再計算。

師：請等一下，十位上分明是3，為什么你說是2？

生7：因為個位向十位借了1，十位需要退位，所以十位就是3－1=2。

師：哦，是的。十位上的退位點提醒我們需要退位。十位上是2減8又不夠減，得向百位借1再計算。究竟怎么算呢？

生8：十位向百位借得1，與十位上原有的2合成12。十位上就是12－8=4，所以十位上的得數是4。

師：最后就得計算百位了，百位上怎么計算？

生9：百位上是3。

師：你是怎么知道的？說說你的理由。

生9：百位上的4退位1，就是3。

師：通過剛才的計算，我們可以得到435－86= 349。現在請同學們幫剛才這位結果是359的同學找找看，他錯在哪里了，并幫他找到出錯的原因。

生10：他計算時十位上出錯了。個位向十位借了1，十位上忘記退位了。

師：是的，我們在計算過程中一定要記得退位。剛才老師說，計算435－86比計算435－18難，你覺得難在哪里？

生11：在計算435－86時，個位和十位均需要向前一位借1。

師：說得很好，這就是我們今天要學習的連續退位減法。（板書課題：連續退位減法）你們都知道怎樣計算連續退位減法了嗎？請你們動筆試一試。

板書：

844－21353－123354－66480－85

133－74261－52278－75406－102

（學生獨立練習并核對答案）

師：大家都算對了嗎？你們有沒有發現，我們容易出錯的都是這些需要退位的地方。（學生點頭表示同意）那老師教你一個小竅門，掌握了它，估計你以后就再也不會出錯了。在計算時一看到這些數字頭上有借位點，馬上減1。也就是“頭上有點就減1”。

設計意圖：主動暴露學生的錯誤，加深學生對這一錯誤的印象，再通過總結口訣“頭上有點就減1”強化正確的退位方式。

3.計數器直觀演示個位如何借1。

師：剛才我們已經學習了連續退位減法，不知道你們掌握得怎么樣，我這里有一個比較難的問題想考考你們。（板書：403－158）

（生獨立計算，師展示錯誤答案：403-158=255）

師：這位同學的計算正確嗎？我們也一起來算一算。豎式計算要注意相同數位對齊，從個位算起，個位上是3減8，不夠減，怎么辦呢？

生12：得向十位借1。

師：向十位借1，會遇到困難嗎？十位能借到嗎？

生12：借不到。

師：是啊！十位上是0，那怎么辦呢？

生13：可以向百位借。

師：百位上不是0，那肯定能借到。那從百位借1之后，十位上是幾呢？

生：10、9。

師：到底是幾呢？我們可以借助計數器幫助理解。（計數器演示：個位不夠減，向十位借；十位是0，向百位借，十位向百位借1，百位退1，十位加10，如圖3、圖4）現在十位上有10個十了，可以借給個位了，借1給個位，十位上是幾呢？接下來該怎么算？

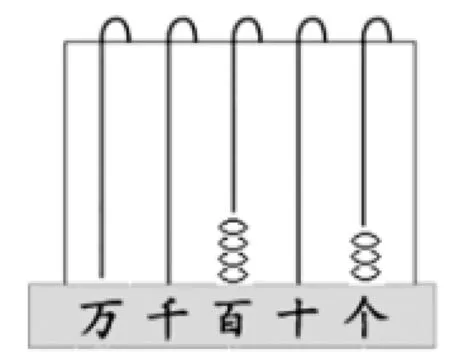
圖3

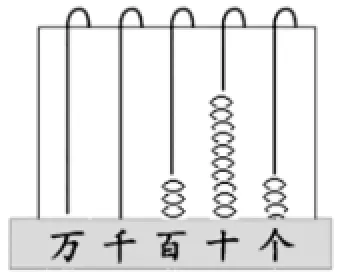
圖4

生14：十位上是9。個位從十位借1，與個位上的3合成13，（師演示，如圖5）13－8=5，個位上的得數就是5。十位上就是9－5=4。

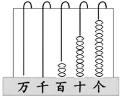
圖5

師：算得很對。那百位上該怎么算呢？結果是多少？

生15：百位上是3－1=2。所以正確的答案是245。

師：很好，現在請大家觀察一下，剛才老師說“頭上有點就減1”，那0上有點就是幾呢？

生16：0上有點就是9。

師：是的，0上有點看作9。（板書）其實，不僅需要看作9，還要記得向前一位借1。

設計意圖：在教學被減數中間有0的減法時，學生學會如何處理被減數中間有0的情況并理解“借1當10”的意義是本節教學內容的重點和難點。教師利用計數器進行直觀演示，使學生清楚地看到個位如何向十位上的0借得1的過程，理解“借1當10”的意義，從而避免出現“跨位借”的現象。

三、討論

1.對總結口訣的思考。

在連續退位減法的教學中，很多學生很難做到知行合一，因忘記退位而頻繁出錯，因此老師們會創編計算口訣，利用這些口訣提醒學生退位，從而提高學生的計算正確率。我們在教學本節內容時，為了避免學生忘記退位導致計算錯誤，也創編了“頭上有點就減1”的口訣，從而提醒學生要退位。從教學效果來看，學生的正確率得到了提高。由此可以看出，運用口訣輔助教學有利于化解教學中的一些難點問題。

但是，有些口訣缺乏延續性，使得學生在后續學習中產生誤解。在教學三位數的連續退位減法時，學生出現了“跨位借”的情況，我們從教材及教師的教學中發現，出現“跨位借”的原因是，學生在二年級學習兩位數退位減法時，教師過于強調“不夠減就向前一位借1”和“借1當10”，使學生形成了思維定式。

綜上所述，口訣對計算教學而言，可以化解一些教學難點，同時也存在一定的缺陷。當學生因為口訣的負遷移產生錯誤時，我們不能一味地責怪學生，而應該關注教材，研究學生學過哪些與之關聯的知識，思考教師在教這些關聯知識時的教學路徑，進而從中尋找出解決問題的方法。

不僅在計算教學中如此，在人教版教材三年級上冊第15頁例題4（如圖6所示）用加法估算解決問題的教學中，學生也不會使用估算正確地解答（如圖7所示）。我們從教材及教師的教學中發現，學生不會將239估算成230的根本原因是，教師在教學二年級下冊第91頁例題10中過于強調用四舍五入法求近似數。諸如此類問題，教師在教學時應引起重視。

圖6

圖7

2.計算教學需要注意的兩個問題。

（1）正確看待問題情境在計算教學中的價值。

《數學課程標準（2011年版）》要求學生能夠結合具體情境，解決實際問題。創設一個好的問題情境引入教學無疑是有利于教學的，但是在計算教學中，有些老師一味地渲染問題情境，致使學生提出了很多與本節課教學無關的問題。教師在處理這些無關問題時沖淡了本節課的教學重點“如何計算”，降低了教學效率。也有教師將計算教學重點傾向于問題解決，花費大量的時間從情境中得出一個算式，脫離了本節課的教學重點“如何計算”。綜上所述，在計算教學中，情境一定要為教學服務，不能因為創設情境而脫離教學目標。

（2）計算教學中應保證學生有充足的練習時間。

計算是一種技能，是需要時間來訓練的。在計算教學中，給學生留有充足的時間進行課堂練習是很有必要的。在教學中，教師該怎樣才能勻出充足的時間給學生練習呢？事實上，在教學某些重難點內容時，當學生無論如何都探究不好時，教師應充分發揮其主導作用，以通俗的講解代替學生的合作探究，這樣便可以節約大量的時間，將勻出的時間讓學生進行鞏固練習，從而達到良好的教學效果。

（執筆：高業波、李暉、劉慧、羅鳳、易楊、徐旺、李闖）