基于課程資源視角的“說數學”活動案例探究*

基于課程資源視角的“說數學”活動案例探究*

☉廣東省廣州市鐵一中學 鐘進均 于曉聞

一、引言

《普通高中數學課程標準》（實驗）（簡稱“標準”）在“課程目標”中明確指出，提高數學地提出、分析和解決問題（包括簡單的實際問題）的能力［1］，數學表達和交流能力，發展獨立獲取數學知識的能力.1981年英國《Cockcroft報告》指出，教數學的主要理由在于“數學提供了有力的、簡潔的和準確無誤的交流信息的手段”［2］.可見培養和提高學生的數學交流能力十分必要.數學交流可分為口頭交流和書面交流.“說數學”［3］屬于前者，是指個體用口頭表達自己對數學問題的具體認識、理解，解決數學問題的思路、思想和方法以及數學學習情感、體會等的數學學習活動.它包括“說知識”、“說過程”、“說異見”和“說體會”.它們分別指口頭表達具體的數學知識，個體解決某數學問題的過程，口頭表達個體對數學問題的結果的不同看法，個體探究某數學問題后的情感體會.

課程資源也稱教學資源［4］，就是課程與教學信息的來源，或者指一切對課程和教學有用的物質和人力.長期以來，我國的課程資源的來源單一，開發主體、實施空間、資源內容等方面的發展也較為落后.廣大一線教師極少參加課程資源開發，較多依賴教材和教學輔助資料；實施空間僅僅將教學局限于課堂；內容往往偏重于知識特別是學科知識的開發，忽視對學生能力、素質的培養，內容結構單一，不利于學生的發展.

“說數學”是一種開發與拓展課程教學資源的教學方式.筆者立足教學實踐，運用案例研究法對“說數學”活動案例從課程資源開發與拓展的角度展開了探究.

二、基于課程資源視角的高中說數學活動案例探究

案例是指包含有某些決策或疑難問題的教學情境故事，這些故事反映了典型的教學思考力水平及其保持、下降或達成等現象；是對個體對象、決策行為、或對某個實踐中發生的情景的真實描述.案例研究需遵循的原則有：①典型性原則：以小見大，反映出某一類事物或教育活動的基本共性.②真實性原則：所描述的是已發生的事實，不虛構.③個性化原則：案例所描述的事件要有一定的特性.④啟發性原則：所描述的事件有一定的沖突，使人產生認知上的不平衡，引發人們深思.⑤創造性原則：符合新課程提倡的教學理念，用新的思考方法、新的觀點去分析研究，得出新的結論或發現新的規律.⑥理論聯系實際的原則：描述的是一個實踐的過程，但反映的卻是理性的問題.

（一）案例描述

筆者任教于廣東省國家級示范性高中，生源水平較好，學生的學習動力足，數學基礎較好.在平時教學中，筆者經常采用“說數學”教學方式進行教學，鼓勵學生大膽“說數學”，課堂氣氛活躍、民主.以下案例來自高三理科數學復習課，具有典型性、真實性、啟發性和創造性.為了確保案例的真實性，以下師生的對話盡量保持原形.

一次數學連堂課給筆者留下了十分深刻的印象.在數學測試卷上有一道題（該卷共有12個小題，此題為第11題）：已知矩形ABCD的邊AB=4，AD=1，點P為邊AB上一動點，則當∠DPC最大時，線段AP的長為（）.

A.1或3B.1.5或2.5

C.2D.3

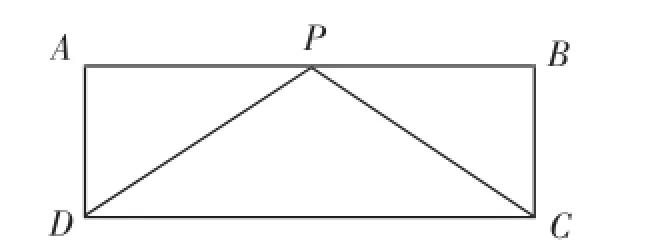
圖1

筆者在講評該測試題時先在黑板上作出圖1，然后在黑板上邊分析題目，邊板書解題過程，具體如下（記為“方法1”）：如圖1，設AP=x，則PB=4-x.因為ABCD是矩形，所以∠PAD=∠CBP=90°.在Rt△DPA中，tan∠APD==

所以tan∠DPC=tan［π-（∠CPB+∠APD）］=-tan（∠CPB+∠APD）=

所以當x=2時，∠DPC最大.因此，答案為C.

在講解完上述方法1之后，筆者問全班學生：“此題還有其他解法嗎？”.沒有學生提出意見.筆者問：“大家看看這條件‘矩形ABCD’，你會想到什么方法？”.筆者見到仍無學生想到其他方法，就提示說：“坐標法.”此時，有多個學生說：“對哦！”筆者問：“那該如何做啊？”平時成績處于中上水平的學生Z說：“老師，我知道怎么做了，讓我來給大家講講吧，可以嗎？”筆者說：“好的，你在黑板板書出來，講解一下.”學生Z在黑板上很快寫下了解題過程，具體如下（記為“方法2”）：以A為原點，分別以AB，AD所在直線為x，y軸，建立平面直角坐標系.設AP=λ，則有P（0，λ），D（1，4），C（1，0），所以=（1，4-λ）=（1， -λ）.故cos∠然，學生Z停下來，思考片刻后轉身看著全班同學說：“我往下不知道如何做了，不會化簡.”顯然，①式的化簡比較麻煩，運算量偏大.筆者對全班學生說：“Z同學的解答思路完全正確！坐標法應用于解答平面幾何問題比較常見.ABCD是矩形為建立平面直角坐標系帶來了方便.至此，本方法能否繼續往下做并得出最終解答，我不敢肯定.若繼續往下做，則需較強的代數式變形技能.至此，問題已轉化為求以λ為自變量的函數最值問題.盼望各位要重視運算變形的訓練.請大家課后繼續完成后續解題過程，看看能否求出最終解答.”當時比較多學生對方法2都做了筆記.之后筆者繼續講評其他試題.出乎筆者意料的是，大約過了20分鐘，在即將下課的時候，平時數學成績特別優秀的男生W對筆者說：“老師，我將剛才的方法2的解答求出來了，這方法確實可得出解答的.”筆者說：“太好了！你拿來給我看看，并講解給我聽.”此時，下課了.筆者安排學生下課休息.在課間，筆者看著男生W做在草稿紙上的解答，聽著他在旁邊認真講解具體如下令x=（λ-2）2，則cos∠DPC=因為函數y=cosx在［0，π］上為減函數，所以要∠DPC最大，則需要最小，即要（x-3）2+16最小.因為λ∈［0，4］，所以x∈［0，4］，所以當x=3時，cos∠DPC的最小值為0，也就是當λ=2，即AP的長為2時，∠DPC最大.看到這里，筆者認為該解答基本上沒什么問題.此時，上課鈴響了，筆者請學生W到黑板詳細寫下上述解答，再面向全班同學講解了一遍.突然，平時愛發問的女生H問：“我看不懂你怎么將cos∠DPC進行轉化的，你是如何想到要如此做的呢，這么煩瑣？”筆者說：“對！請W具體介紹你是如何想到這樣做的.”學生W接著繼續在黑板上邊板書邊講解：“分母（λ2-8λ+17）（1+λ2）=λ4-8λ3-18λ+17=［（λ-2）2］2-6（λ-2）2+25.（*）”筆者追問：“你怎么想到將λ4-8λ3-18λ+17轉化成［（λ-2）2］2-6（λ-2）2+25的呢？這么復雜的式子！”W邊寫邊說：“［（λ-2）2］2=λ4-8λ3+24λ2-32λ+16，（**）又（λ-2）2=λ2-4λ+4.我對比λ4-8λ3+18λ2-8λ+17和（**），就容易想到-6（λ-2）2=-6λ2+24λ-24，（***）到此，（*）就可配湊得到了”.此時，教室里響起了熱烈的掌聲.個別學生自發地說：“太厲害了！”筆者說：“很有道理.我自己也很難做得有你如此優秀啊，佩服佩服！這么煩瑣、復雜的問題都被你解決了，有何感受體會啊？”學生W說：“我自己之前沒有想過用老師介紹的這坐標法去解.在上一節課老師提到了這個方法，確實入手很容易的.可是老師說到了，往下很難轉化來求出最值.我就嘗試去做一做，難度真的很大，有挑戰性.不過我堅信這方法一定能求解到解答的.還有，如果真的做不出來，我就考慮求導的方法了，只是對cos∠DPC求導更加煩瑣了.在做的過程中，我也想過放棄，覺得很煩瑣的，但內心又有點不甘.我按照老師以前教的方法和思路去做，不斷想辦法將分子化成常數；只要做到如此，那就一定能求出結果的.通過這一解題過程，我內心很高興的，感到很自豪，挑戰了一下自己，挺爽的，執著很重要！”筆者接著說：“學生W一直都是我們班的數學成績很優秀的同學.大家很容易看到他對數學很執著，不畏難，不輕易放棄，很值得大家學習！我們再用掌聲感謝他.”至此，這習題的講解結束了，共耗掉了至少25多分鐘.

（二）案例分析

1.說數學是一種創造交流性課程資源的教學方式

“交流”就是“互相溝通”［6］.說數學是學生之間、教師與學生之間進行知識與技能，過程與方法，情感、態度與價值觀等交流的重要渠道.從知識的表征角度看，“數學知識可分為陳述性知識、程序性知識和過程性知識等三類.陳述性知識是關于事實的知識，是人所知道的有關事物狀況的知識.程序性知識是關于人怎樣做事的知識，即由完成一件事所規定的程序、步驟及策略等組成的知識”，“過程性知識是伴隨數學活動過程的體驗性知識.它是一種內隱的、動態的知識；沒有明確地呈現在教學材料中，而是隱性地依附于學習材料，在學習的過程中潛在性地融會貫通；始終伴隨著知識的發生和發展過程，學習者只能在學習的過程中去體驗，體現出過程性知識的動態性”［7］.

通常，數學教師非常重視課本、練習冊、習題卷和作業本等教學資源的選取和使用.課本是數學教學的重要資源和工具.批改作業（含練習冊、習題卷和作業本）是師生之間進行知識性交流的重要方式.傳統的作業較多呈現的是學生的陳述性知識和程序性知識情況，較少反映學生的過程性知識情況，也就是讓老師知道學生的解答是否正確，但無法得知“對”與“錯”的背后的“艱苦付出”和體會.許多老師在課堂上通過提問與學生交流，較多關注學生所回答的具體知識（結果）或者解題過程是否準確，而較少關注這些“結果”是如何得來的，也就是，教師開發交流性資源的意識不足.

上述案例，筆者介紹完方法1之后，故意設計了一個環節：提出另外的解題方法（努力方向），但是沒有給出具體解答過程；考慮到這個班的數學基礎較好，讓學生課后去嘗試求解出答案.想不到學生W“抓住不放”，在課堂上認真地完成了后續解答，筆者積極鼓勵他在講臺上呈現自己的解題過程，鼓勵其他學生發問，使得數學課堂充滿了數學交流：既有師生之間的交流，也有學生與學生之間的交流.在回答其他學生的發問過程中，W非常具體地說出了自己的思維歷程（“說過程”）.在同學和老師的追問下，W說出了自己的解答過程中的每一步是如何得來的（“說過程”）.因此，學生們從W的板書學習到了“陳述性知識”，從他的“說”學習到了“程序性知識”.在筆者的啟發引導下，W說出了自己克服困難，不懈努力去轉化cos∠DPC的表達式，最終成功求解的感想和體會（“說體會”），亦即W“說”出了“過程性知識”.從而，W的“寫”與“說”相結合，邊“寫”邊“說”，在“寫”的基礎上再用“說”來補充與提升，促進了他與老師、其他學生之間的交流.客觀地說，如果上述方法2的解答，如果沒有W的“說”，確實不易理解，也正是W的“說”表明他對這問題及其解答的認識十分深刻.可見，“說數學”創造了數學課堂的交流性課程資源，不僅交流了知識（陳述性知識和程序性知識），還交流了感想和體會（過程性知識）.

2.說數學有助于拓展反思性課程資源

“拓展”是指“開拓擴展”［6］.反思是指思考過去的事情，從中總結經驗教訓.反思性課程資源是指能促進師生進行反思的課程資源，對學生而言，主要是對自身數學學習情況的反思；對教師而言，主要是對數學教學情況的反思.反思性數學學習就是學習者對自身數學學習活動的過程，以及活動過程中所涉及的有關材料、信息、思維、結果等學習特征的反向思考.教學需培養學生的反思意識，讓學生形成反思習慣.傳統的反思性學習資源較多是課本、測試卷、作業等.這些資源較多反映“結果”，難以反映“過程”和“體驗”.因此拓展反思性資源很有必要.

在上述案例中，學生Z寫下了方法2的前面部分解題過程，無法將①進行化簡求出最值，引發了他和其他學生的反思：一是這方法及其解答過程和方法1的區別在哪里；二是①式有錯誤嗎，為什么求不出最值呢？學生W的解答引起了女生H的發問，促進了學生W的深入反思.學生W的“說過程”和“說體會”必需他本人充分反思解題過程、結果以及體驗，否則無法說出來.“說數學”促進了學生從解題結果到過程（含思想方法），再到體驗的反思.因此，“說數學”有助于拓展反思性課程資源.

3.說數學能開發拓展性課程資源

“說數學”是一種開發拓展性課程資源的教學方式，主要是指以下兩個方面：

第一，“說知識”可以是對課本知識（或課堂內容）的延伸、拓展.上述案例中的方法2就是對課堂內容的延伸和拓展，與筆者詳細講解的方法1完全不同.方法1從正切函數及其變換角度切入，構造函數，接著轉化為二次函數再討論其最值；方法2先建立平面直角坐標系，得到點的坐標，然后將線段的夾角轉化為向量的夾角來求解，計算量增大，恒等變形的技巧性增強，而“坐標法”是一種十分重要的幾何問題求解方法.因此，通過“說”方法2，就學生而言，無論是“說者”還是“聽者”都加深了對案例中的問題本身及其解法的認識.

第二，“說數學”開發了課程評價資源.課程評價是教學的重要組成部分.教師要高度關注學生數學學習的情感、態度與價值觀，而學生的情感、態度與價值觀往往是隱性的，伴隨在數學學習過程當中.長期以來，教師如何更好地培養學生正確的數學學習情感、態度與價值觀，是一個很值得深入研究的課題.“說數學”是實施數學教學評價的重要方式之一［9］，能拓展評價內容和方式.正如前面所述，學生W僅提供詳細的書面解題過程，其他學生甚至老師都未必能理解.如果沒有W的“說”，僅看其書面解答結果，那么我們就無法知道其解題思維歷程和心理體驗.正是“說知識”、“說過程”和“說體會”，讓W的情感、態度與價值觀盡量顯性化，讓教師有機會對其給予激勵性評價.所以，“說數學”開發了拓展性課程評價資源.

三、結束語

“說數學”［10］是一種老師引導、參與開發校本數學課程資源的教學方式.筆者在長期的“說數學”實踐中收集了不少案例，也就積累了許多寶貴的教學資源.創設機會讓學生“說數學”其最大意義和價值在于引導和促進教師和學生真正從基于教科書的教與學轉向基于數學課程資源的教與學.課程資源的開發對教師提出了新的專業能力要求［11］，譬如，我們應該如何開發優質課程資源更好服務于培養學生的數學核心素養，就很值得深入探究.

1.葉堯城.高中數學課程標準教師讀本［M］.武漢：華中師范大學出版社，2003，9.

2.范良火譯.數學算數—英國學校數學教育調查委員會報告［R］.北京：人民教育出版社.1994.

3.鐘進均.在高中數學教學中開展說數學活動的實驗研究［J］.數學教育學報，2008，17（5）.

4.張廷凱，豐力.校本課程資源開發指南［M］.北京：人民教育出版社，2004，1.

5.鄭金洲.教育研究專題［M］.上海：華東師范大學出版社，2002，3.

5.鐘進均.在高中數學教學中開展數學交流活動的實驗研究［D］.云南師范大學，2008.

6.商務印書館次數研究中心.新華詞典［M］.北京：商務印書館，2001，4.

7.喻平.數學教育心理學［M］.南寧：廣西教育出版社.2004.8：.

8.涂榮豹.試論反思性數學學習［J］.數學教育學報，2000，9（4）：.

9.鐘進均.高中“說數學”的過程性評價探究［J］.中學數學教學，2010（6）：6-9.

10.鐘進均，劉仁森.基于需求層次理論的“說數學”案例探究［J］.中學數學（上），2015（6）.

11.鐘進均.基于課程資源視角的數學日記探究［J］.中國數學教育，2013（6）.

*本文為廣州市教育科學“十二五”規劃課題《基于認知心理學視角的高中說數學活動案例探究》（課題批準號1201542650）和廣州市教學成果培育項目《基于課程資源視角的數學日記探究》（M2015A077）的階段性研究成果.