高考函數導數壓軸題分析及應對策略

高考函數導數壓軸題分析及應對策略

☉廣東省鶴山市第二中學 李立美

函數與導數是高中數學中極為重要的內容，其觀點和方法也經常用于解決其他非函數類型的問題.其主要從以下幾點進行考查：1.導數的概念以及利用導數解決一些簡單類型的題目，如求極值，最值，切線方程，單調區間等；2.綜合考查，將導數的內容與其他知識有機地結合起來，設計綜合題.

從近幾年高考函數與導數的大題得分情況來看，考生的得分普遍偏低.筆者通過近幾年的教學實踐，發現對于函數與導數的題目，學生普遍反映的主要問題有兩個：一是思路不清晰；二是對解答函數與導數題目的方法掌握得不夠，即使知道有幾種方法，但是遇到具體題目時無從下手，不知選擇何種方法.筆者從近幾年的高考卷中選擇幾道壓軸題，利用思路線幫助厘清答題思路，并且探討高考數學函數與導數的答題方法.

策略一、轉化與化歸的運用

例1已知函數（fx）=2x3-3x.若過點P（1，t）存在3條直線與曲線y=（fx）相切，求t的取值范圍.

解：設過點P（1，t）的直線與曲線y=（fx）相切于點（x0，y0），則y0=2-3x0，即切線的斜率為k=6-3，所以切線方程為y-=（6-3）（x-x）.將點P（1，t）代入，得t-y=（6x2-000 3）（1-x），整理得4-6+t+3=0.于是問題轉化為此方程

0有三個不同的解.設g（x）=4x3-6x2+t+3，則“過點P（1，t）存在3條直線與曲線y=（fx）相切”等價于“函數g（x）有3個不同零點”.

因為g′（x）=12x2-12x=12x（x-1），

當x變化時，g（x）與g′（x）的變化情況如下：

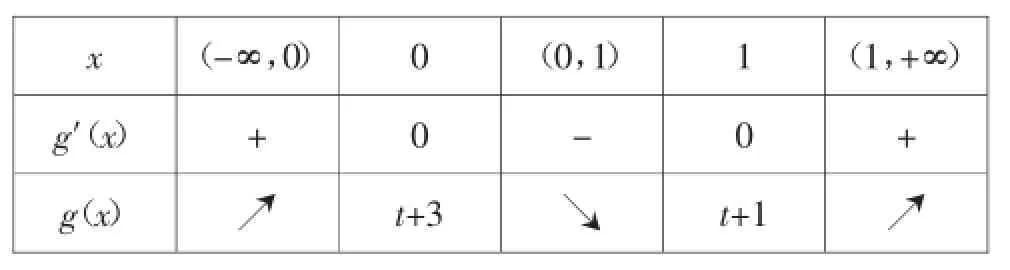
x（-∞，0）0（0，1）1（1，+∞）g′（x）+0-0+ g（x）↗t+3↘t+1↗

所以，g（0）=t+3是g（x）的極大值，g（1）=t+1是g（x）的極小值.

當g（0）＞0且g（1）＜0，即-3＜t＜-1時，因為g（-1）=t-7＜0，g（2）=t+11＞0，由于g（x）在區間（-∞，0），（0，1），（1，+∞）上單調，故g（x）分別在區間（-1，0），（0，1）和（1，2）上各有1個零點，即g（x）分別在區間（-∞，0），（0，1），［1，+∞）上各有1個零點.

綜上可知，當過點P（1，t）存在3條直線與曲線y=f（x）相切時，t的取值范圍是（-3，-1）.

在研究、解決數學問題時，采用某種手段或方法，使問題從一種情形轉化為另一種情形，也就是轉化到另一種情景使問題得到解決，這種轉化是解決問題的有效策略，同時也是一種成功的思維方式.轉化具有多樣性、層次性和重復性的特點，遵循熟悉化、簡單化、直觀化的原則.本題的轉化，使切線的條數轉化為函數的零點個數，為解題鋪平了道路

策略二、分離參數

分析：已知f（x）在（0，2）內存在兩個極值點，求k的取值范圍，無法直接求解，需要進行轉化.函數f（x）在（0，2）內存在兩個極值點?導數f′（x）=0在（0，2）內有兩解?分離參數?y=k與y=g（x）在（0，2）內有兩個交點?由g（x）的導數求極值點作出滿足條件的圖像?求出參數范圍.

解：因為函數f（x）在（0，2）內存在兩個極值點，

當x變化時，g′（x）與g（x）的變化情況列表如下：

（0，1）1（1，2）g′（x）-0+ g（x）單調遞減極小值單調遞增

分離參數法是我們經常用到的一種方法.在解答的過程中思路清晰，其關鍵同樣在于轉化以及利用極值作出函數圖像，利用數形結合.

策略三、最值法

（1）求a，b；

（2）證明：f（x）＞1.

分析：由題可得f（1）=2，f′（1）=e，進而求出a，b；第（2）問題屬于證明題，不等式左邊比較麻煩，需要對不等式進行化簡，再證明.

解：（1）略.

（2）證明：將不等式轉換成g（x）＞h（x）的形式?［g（x）］min＞［h（x）］max.

所以g（x）＞h（x），即f（x）＞1.

此種方法對于一些既含有指數函數，又含有對數函數的題目比較實用，通過化簡將它們分離，對于后面求最值降低難度.但此種方法需要進行合適的變形，這時需要讀者多嘗試幾種變形.

策略四、構造函數

例4已知函數f（x）=-2（x+a）lnx+x2-2ax-2a2+a，其中a＞0.

（1）設g（x）是f（x）的導函數，討論函數g（x）的單調性；

（2）證明：存在a∈（0，1）使得f（x）≥0在區間（1，+∞）內恒成立，且f（x）=0在區間（1，+∞）內有唯一解.

解析：（1）（略）.

（2）證明：由f（′x）=2（x-a）-2lnx-2（ 1+）=0，解得a=

當a=a0時，有f′（x）=0，f（x0）=φ（x0）=0，由（1）知，f′（x）在區間（1，+∞）上單調遞增，故當x∈（1，x0）時，f′（x）＜0，從而f（x）＞f（x0）=0；當x∈（x0，+∞）時，f′（x）＞0，從而f（x）＞f（x0）=0.所以，當x∈（1，+∞）時，f（x）≥0.

綜上所述，存在a∈（0，1），使得f（x）≥0在區間（1，+∞）內恒成立，且f（x）=0在區間（1，+∞）內有唯一解.

構造函數是解決導數問題的常用手段，巧妙地構造函數能使我們對問題有更加深刻的認識，是解題的銳利武器.常用的構造方法有移項作差、結構抽象、確定主元等.本題的匠心之處在于兩次構造函數.尤其是第一次以解代參，即以f′（x）=0時的a值代替f（x）中的參數a構造函數φ（x），它在（1，e）上有零點，且當a=a0時，有f′（x）=0，f（x0）=φ（x0）=0是解題的關鍵.

策略五、設而不求

又f′（-1）＜0，f′（0）＞0，故f′（x）=0在（-2，+∞）上有唯一實根x0，且x0∈（-1，0）.當x∈（-2，x0）時，f′（x）＜0；當x∈（x0，+∞）時，f′（x）＞0，從而當x=x0時，f（x）取得最小值.

由f（′x）0=0，得ex0 =，ln（x0+2）=-x0，故（fx）≥（fx）0

例5已知函數f（x）=ex-ln（x+m）.當m≤2時，證明f（x）＞0.

證明：當m≤2，x∈（-m，+∞）時，ln（x+m）≤ln（x+2），故只需證明當m=2時，f（x）＞0.當m=2時，函數f′（x）=ex-

綜上，當m≤2時，f（x）＞0.

求方程f′（x）=0的根在解導數問題中是承上啟下的一步，此時受阻，解題將難以為繼.像本題中，雖然f′（x）= 0的根的確存在，可無論如何都求不出來.怎么處理？上述解答告訴我們，可以虛設零點，但設而不求，只利用其滿足的條件就能到解題目的.這種“設而不求”的方法，在數學中是經常遇到的，特別是解析幾何中直線與圓錐曲線的交點.

策略六、分類討論

例6已知函數（fx）=x2-ax（3a＞0），x∈R.

（1）求f（x）的單調區間和極值；

（2）對于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）·f（x2）=1，求a的取值范圍.解：（1）單調遞減區間為（-∞，0）和（，+∞），單調遞增為

+∞），都存在x2∈（1，+∞），使得（fx）1·（fx）2=1”等價于A?B，顯然，0?B.

下面分三種情況討論：

分類討論是將一個較復雜的數學問題分解成若干個基礎性問題，通過對基礎性問題的解答來實現解決原問題的思維策略.分類討論要堅持不重不漏、標準統一的原則.分類討論的步驟是：確定對象、合理分類、逐類討論、歸納總結.本題中，兩個集合A、B中的元素是倒數關系，能否取導數取決于它是否為零.又因為x1∈（2，+∞），∈（1，+∞），所以按照＞2、1≤≤2、＜1三種情況討論.

總之，導數及其應用是高中數學的重要內容，是進一步學習高等數學的重要基礎.在高考試卷上，它是以壓軸題的形式呈現的.由于其信息量、思維量、運算量都比較大，需要較高的數學分析、解決問題的能力.由以上各例可以看出，上述幾種方法不是相互排斥的，而是相輔相成的.在具體問題中，往往是幾種方法互相配合、共同發力.只要運用得當，就能收到良好的效果.