透過現(xiàn)象看本質(zhì)解題能力自然高

透過現(xiàn)象看本質(zhì)解題能力自然高

☉浙江省柯橋中學(xué) 盧小瑋

數(shù)學(xué)教學(xué)從某種程度上說就是解題的教學(xué).而在我們高三數(shù)學(xué)教學(xué)的課堂上，我們有的數(shù)學(xué)老師存在著就題論題，滿足于完成這一題得出結(jié)果，不能夠讓學(xué)生從茫茫的題海中解脫出來，那“一題多解”“多題一解”，透過現(xiàn)象看本質(zhì)就顯得尤為重要了.教師要誘導(dǎo)學(xué)生多角度、多層次地思考問題，激活學(xué)生思維的發(fā)散性和創(chuàng)造性；可以讓學(xué)生有梯度的深入難點，引導(dǎo)學(xué)生將一些經(jīng)過遷移的交匯知識進(jìn)行歸納總結(jié)，能夠提高教學(xué)的有效性，提升學(xué)生的思維品質(zhì).筆者結(jié)合平時教學(xué)中的幾個案例談?wù)勅绾瓮高^現(xiàn)象，挖掘問題的本質(zhì).

案例1如圖1，已知△ABC，D是AB的中點，沿直線CD將△ACD折成△A′CD，所成二面角A′-CD-B的平面角為α，則（）.

A.∠A′DB≤α

B.∠A′DB≥α

C.∠A′CB≤α

D.∠A′CB≥α

圖1

此題是2015年高考浙江卷理科第8題，它的立意是深刻的.很多老師對此進(jìn)行解讀，主要觀點是：考查“課標(biāo)理念——‘直觀感知，操作確認(rèn)，思辨論證，度量計算’的創(chuàng)新試題”，只要動手進(jìn)行“折紙操作”+“特值法”就能篩選出答案，或者如果直接計算“計算量不是一般的大”；所以不能采取“直接計算方法”，動手進(jìn)行“折紙操作”+“特值法”從數(shù)學(xué)思想方面“一般問題”，特殊化處理，這從考試技術(shù)上應(yīng)該說是一個好的方法，但是我們也應(yīng)該看到，這種方法不是數(shù)學(xué)教學(xué)的真正歸宿.筆者經(jīng)過思考發(fā)現(xiàn)，此題其實是一個定理的特殊情況，下面給出該定理并簡單證明：

定理若點D是△ABC的邊AB上的任意一點（端點A、B除外），沿直線CD將△ACD折成△A′CD，所成二面角A′-CD-B的平面角為α，則∠A′DB≥α.

證明：如圖2，作AM⊥CD，BN⊥CD，垂足分別為M，N，BE∥CD，交AM的延長線于點E，連接EM，EN.

圖2

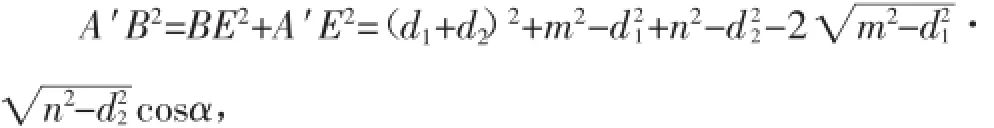
所以∠A′DB≥α.

由此可見，證明也并不復(fù)雜，高考題只是定理的特殊情形（m=n）！因此可以看出命題專家所給出的“條件”點D是AB的中點，即AD=BD是多余的！這可能才是本題的真正本質(zhì)所在！因此作為數(shù)學(xué)教師，對于自己一時無法解決或難以解決的問題，不能給學(xué)生設(shè)置“禁區(qū)”束縛學(xué)生的思維，而應(yīng)實話實說，給自己和學(xué)生都留有思考的“空間”，也只有這樣才能培養(yǎng)學(xué)生勇于探索的精神，不斷提高學(xué)生的創(chuàng)新能力.

案例2在△ABC中，G為△ABC的重心，且AG⊥BG，則sinC的最大值為_______.

這是鹽城市高三的一道調(diào)研試題.考試過后，筆者所任教班級里的學(xué)生普遍反映：題目比較陌生，信息量很少，不知道切入點在哪，很茫然.可事實是否真的如學(xué)生所說呢？下面筆者給出解決此題的幾個切入點.

切入點1：根據(jù)垂直的條件AG⊥BG.

根據(jù)AG⊥BG這一條件，我們很容易想到建系，將幾何問題代數(shù)化解決.建立如圖3所示的平面直角坐標(biāo)系.設(shè)A（0，a），B（b，0），因為G為重心，易得C點坐標(biāo)為（-b，-a）.

在建系的前提下，我們又可以嘗試以下兩種方法：

圖3

方法1：利用余弦定理和基本不等式可知，

這兩種方法本質(zhì)上都是建系尋找到點的坐標(biāo)之間的關(guān)系（本質(zhì)上是三邊之間的關(guān)系），然后利用余弦定理和基本不等式解決問題.

事實上我們還可以通過以下的兩種方法去尋找到三邊之間的關(guān)系.

方法3：在直角△AGB、△AGE、△BGD、△DGE中，分別利用勾股定理易得BC2+AC2=5AB2，再用余弦定理和基本不等式易得結(jié)果.

從上面這些方法我們可以發(fā)現(xiàn)，抓住垂直這一條件，結(jié)合平時處理垂直的常用手法，可以從多個方向進(jìn)行突破.

切入點2：G為△ABC的重心.

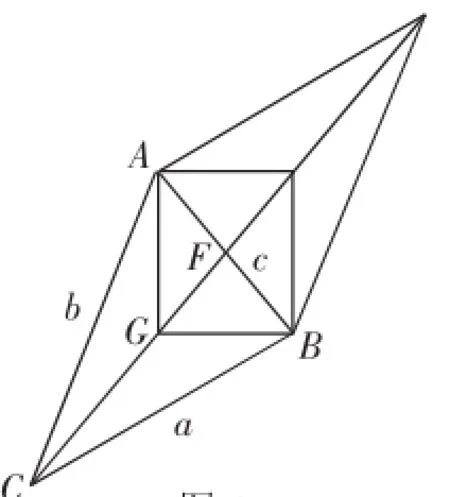
圖4

方法5：如圖4，因為G為△ABC的重心，

題目中給出的條件也一樣.G為△ABC的重心和AG⊥BG這兩個條件也不應(yīng)該是孤立的條件.

切入點3：G為△ABC的重心和AG⊥BG合二為一.

我們知道對于重心還有一個比較重要的幾何性質(zhì)：DG∶GA=1∶2.

將AG⊥BG這一條件和圓中的知識聯(lián)系起來就有了如下的幾何方法：如圖5所示，不妨設(shè)小圓和大圓的半徑分別為1和3，點C為大圓上一點，連接OC交小圓于點G，則△ABC即為滿足題意的三角形.題目即轉(zhuǎn)化為點C在圓上運動時，要使角C最大，由著名的米勒定理可知，當(dāng)過點A，B的圓與點C的軌跡即大圓相切時，角C最大.

圖5

圖6

如圖6所示，顯然當(dāng)點C在y軸上時，角C最大，此時易得sinC=

橫看成嶺側(cè)成峰，透過現(xiàn)象看本質(zhì)，形成探究意識，培養(yǎng)探究能力.通過上面這些解決問題的切入點和方法的選擇，我們發(fā)現(xiàn)在平時的教學(xué)中應(yīng)該鼓勵學(xué)生多從條件入手，結(jié)合常見的處理方法認(rèn)真分析條件，努力尋找問題的突破口.

（1）求橢圓的方程；

（2）設(shè)P是橢圓C上一點，直線PA與y軸交于點M，直線PB與x軸交于點N，求證：|AN|·|BM|為定值.（2016年北京高考理科第19題）

解析幾何較歐氏幾何，最大的優(yōu)勢是把“運動變化引入數(shù)學(xué)”，使我們實現(xiàn)了“用坐標(biāo)刻畫運動”這一基本代數(shù)手段來研究幾何問題的設(shè)想.直線與圓錐曲線位置關(guān)系中的運動變化，一般點或直線遠(yuǎn)動變化是根源，如果我們很好地把握了這個根源，選擇好從點入手還是從直線入手，就能很好地簡化計算過程，快速地解決此問題.

圖7

（2）證明：由（1）知，A（2，0），B（0，1），設(shè)P（x0，y0），則x

當(dāng)x0≠0時，直線PA的方程為

令y=0，得xN=-

當(dāng)x0=0時，|BM|=2，|AN|=2，|AN|·|BM|=4.

本題中，|AN|和|BM|是兩個變量，要我們證明在這個變化過程中|AN|·|BM|為定值，如何證明這個事實？顯然要把|AN|和|BM|用某種變量表示出來，在通過代數(shù)運算得出|AN|·|BM|為定值，那么引入什么變量？研究本題發(fā)現(xiàn)，|AN|和|BM|兩個量隨點P的變化而變化，點P的運動變化是本題中其他所有量發(fā)生變化的根源，所以我們設(shè)P（x0，y0），將點M，N的坐標(biāo)用x0，y0表示出來，從而用x0，y0表示|AN|·|BM|，在根據(jù)P（x0，y0）在橢圓上，從而得出| AN|·|BM|為定值.

（2）證明：設(shè)P（x0，y0），直線PA的方程為y=k（x-2）代入+y2=1，得（1+4k2）x2-16k2x+16k2-4=0，

所以2+x0=

所以x0=

在解法2中，采取從直線PA入手，引入直線PA的斜率k，直線方程與橢圓方程聯(lián)系，根據(jù)一元二次方程根與系數(shù)的關(guān)系將點P的坐標(biāo)用直線PA的斜率k表示，再用k表示M，N的坐標(biāo)，從而實現(xiàn)用k表示|AN|·|BM|，最后通過代數(shù)恒等變形得出|AN|·|BM|為定值.本證法是解決圓錐曲線綜合問題的常用方法，思路自然方法熟悉，不過與證法1對比此法運算量較大，學(xué)生得分效果不好.縱觀圓錐曲線綜合問題一般有設(shè)點和設(shè)直線兩種解法，在確定解題思路時要體會解析幾何的知識本質(zhì)，從產(chǎn)生運動變化的根源入手，題目確定從點入手還是從直線入手，這樣可以很好地優(yōu)化解題過程，簡化計算.

總之，在高中教學(xué)中，我們教師要立足課本，回歸課本.從最近幾年的高考試題和高三的模擬試題中可以發(fā)現(xiàn)，有很多題目都有一定的本質(zhì)，都能在可以在課本上找到原型.故我們要強化對課本典型例題、習(xí)題的研究，不能簡單地就題論題，要注重引導(dǎo)學(xué)生進(jìn)行一題多解、一題多變、一題多解，追根溯源，引導(dǎo)學(xué)生從不同的角度去觀察問題、思考問題，從而使學(xué)生的思維從單一走向多維，提高課堂的高效，優(yōu)化他們的思維.