基于關聯視角，實踐“用教材教”
——以“從二次函數視角看一元二次方程”教學為例

☉江蘇南通市易家橋中學 徐向清

基于關聯視角，實踐“用教材教”
——以“從二次函數視角看一元二次方程”教學為例

☉江蘇南通市易家橋中學 徐向清

最近一次教研活動中，筆者有幸執教“從二次函數視角看一元二次方程”研討課，該課沒有簡單照搬教材內容，而是從學生已有經驗出發，先復習一次函數與一元一次方程之間的關系，然后引出二次函數與一元二次方程之間的關系，取得較好的教學效果.本文先整理該課的教學流程，并闡釋教學立意，供分享.

一、“從二次函數視角看一元二次方程”教學流程

教學環節（一）熱身練習，回顧舊知.

（1）一次函數y=2x-6中，當y=0時，求自變量x.

（2）一次函數y=2x-6中，當y=2時，求自變量x.

（3）當一次函數y=2x-6與y=-x+3的函數值相等時，求自變量x.

設計意圖：講評時注意讓學生展示一元一次方程的解，對應著直線（一次函數的圖像）與x軸的交點坐標之間的關系，具體如下：

（1）一次函數y=2x-6中，當y=0時，可得方程2x-6=0，解得x=3.即一次函數值為0時，自變量x=3，此時也可得直線y=2x-6與x軸的交點的橫坐標為3.

（2）一次函數y=2x-6中，當y=2時，可得方程2x-6=2，解得x=4.即一次函數值為2時，自變量x=4，此時也可得直線y=2x+6與直線y=2的交點的橫坐標為4.

（3）當一次函數y=2x-6與y=-x+3的函數值相等時，可得方程2x-6=-x+3，解得x=3.此時也可得直線y=2x-6與直線y=-x+3的交點的橫坐標為3.

預設PPT漸次呈現如下的對應關系圖（如圖1）：

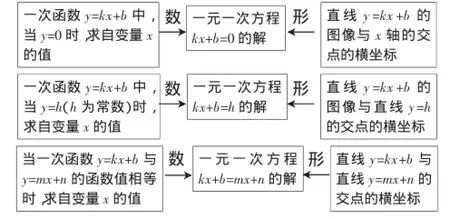
圖1

教學環節（二）兩道問題，探究新知.

問題1：以40m/s的速度將小球沿與地面成30°角的方向擊出時，小球的飛行路線將是一條拋物線.如果不考慮空氣阻力，小球的飛行高度h（單位：m）與飛行時間t（單位：s）之間具有函數關系h=20t-5t2.

（1）小球的飛行高度能否達到15m？如果能，需要多少飛行時間？

（2）小球的飛行高度能否達到20m？如果能，需要多少飛行時間？

（3）小球的飛行高度能否達到20.5m？為什么？

（4）小球從飛出到落地要用多少時間？

思路簡述：將h的值代入二次函數的解析式可以得到關于t的一元二次方程，則根據方程是否有符合實際的解來說明小球的飛行高度能否達到所給的值.

預設講評PPT截圖如同2所示：

圖2

預設點評：通過上述問題的解決，大家從“數”的角度認識到二次函數與一元二次方程的關系：“已知二次函數y=ax2+bx+c的值為0，求自變量x的值”即為“求解一元二次方程ax2+bx+c=0”；反之亦如此.

問題2：下列二次函數的圖像與x軸有公共點嗎？如果有，公共點的橫坐標是多少？當x取公共點的橫坐標時，函數值是多少？你能得出相應的一元二次方程的根嗎？二次函數的圖像與一元二次方程具有怎樣的聯系？

（1）y=x2+x-2；（2）y=x2-6x+9；（3）y=x2-x+1.

思路簡述：x軸上的點的縱坐標均為0，即二次函數的函數值為0，所以可將y=0分別代入二次函數的解析式，可得相應的一元二次方程，根據一元二次方程根的情況即可判定拋物線與x軸的交點的情況.

預設講評PPT（如圖3）：

圖3

預設點評：通過上述問題的解決，可以發現二次函數的圖像與一元二次方程也有關系：（1）拋物線與x軸的交點個數與相應一元二次方程根的情況相關；（2）拋物線與x軸的交點的橫坐標即為相應一元二次方程的兩根.

教學環節（三）練習訓練，鞏固新知.（略）

教學環節（四）課堂小結，梳理歸納.

通過前面的學習，大家可以發現“求一元二次方程ax2+bx+c=0的根”，從數的角度可看作“已知二次函數y= ax2+bx+c的函數值y=0，求自變量x”；從形的角度看“一元二次方程ax2+bx+c=0的根的情況”與“拋物線y=ax2+bx+c與x軸的交點的個數”相關，且“方程ax2+bx+c=0的根”為“拋物線y=ax2+bx+c與x軸的交點的橫坐標”.一邊講解，一邊動畫呈現如下PPT（如圖4）：

圖4

拓展思考：有了前面的學習經歷，可以變式思考如下一些問題：

例如：方程x2-2x+3=6的根，從數的角度可看作二次函數y=x2-2x+3的函數值y=6時對應自變量的值，從形的角度可看作拋物線y=x2-2x+3與直線y=6的交點的橫坐標.同時，結合圖像可以發現拋物線y=x2-2x+3與直線y=2有1個交點，說明方程x2-2x+3=2有2個相等的實數根；拋物線y=x2-2x+3與直線y=1沒有交點，說明方程x2-2x+3=1無實數根.因此“一元二次方程ax2+bx+c=h的根的情況”與“拋物線y=ax2+bx+c與直線y=h的交點個數”相關.

二、教學立意的進一步闡釋

1.理解數學，在數學內在聯系處創設情境、引入新課.

初中數學富含聯系，特別是數式、方程與函數的知識都可統一在函數的高觀點之下，這在八年級學習一次函數之后就能感受出來.學生從一次函數的視角再認識了此前所學的一元一次方程、二元一次方程組、一元一次不等式（組）等知識，“站在高處”俯看舊知別有一番認識在心里.本課沒有沿用教材上的情境引入，而是用所謂“復習舊知”的方式引入新課，但這種復習舊知又不是簡單的知識再現，而是對比了從一次函數視角看一元一次方程，本課所學習的是從二次函數視角看一元二次方程，這樣它們之間的一致性就得到了顯現.

2.設計課件，讓講解、點撥與小結在漸次呈現中助學.

最近《中學數學》（下）不少課例文章中附了課件PPT截圖，對于課堂教學設計中的課件制作提出了有益參考，特別是相關課例中的課件使用了漸次呈現、標注提示等方式，使得課件的功用得到發揮，過渡了不同教學環節，突出了教學重點，化解了教學難點，使得學生的注意力得到提升.這就是我們在上文中也附出幾幅PPT截圖的原因，目的是讓更多的同行能感受到不同教學重點或難點突破的多樣化努力.

3.拓展思考，課堂小結時為學生打開窗戶、向上挑戰.

由于教學時間所限，我們在課堂小結之后給學生拓展視角，把一元二次方程一般式的形式推廣到了方程等號右邊不是0的情形，對應著二次函數圖像與直線y=h相交的情形.這種拓展思考有一定的挑戰，但是對優秀學生來說是可以接受的，因為在八年級學習一次函數時，就曾研究過類似直線y=x+1與直線y=2的交點問題（對應著方程x+1=2）.這里值得一說的是，關于教學深度的話題，即使是新授課，也可以在小結階段結合本課的內容幫助一些優秀學生走向縱深方向，就如同為學生打開一扇窗一樣，而不是“封閉著”，我們需要的是給優秀學生提供深入思考的機會.

三、寫在最后

鄭毓信教授關于數學教師如何才能用好教材提出他的一些深刻見解，歸根結底是需要我們保持獨立思考、深入思考，基于理解數學的高度，拋卻“綱本主義”，基于自己修煉的“善于舉例、善于提問、善于優化”的基本功，認真組織教學內容、規劃教學進程、預設教學課件等，追求更有數學味、更加開放的數學課堂.想來，本文中的課例只是圍繞上述高要求的一次課例實踐，做得還不到位，我們還有很長的路要走.

1.章建躍.構建邏輯連貫的學習過程使學生學會思考［J］.數學通報，2013，56（6）.

2.劉東升.我們需要怎樣的“問題”驅動課堂——由美國莎維女士執教的函數圖像課說起［J］.教育研究與評論（課堂觀察版），2016（11）.

3.鄭毓信.“開放的數學教學”新探［J］.中學數學月刊，2007（7）.

4.鄭毓信.數學教師如何才能用好教材［J］.小學教學（數學版），2016（3）.