思維導(dǎo)圖在初中幾何教學(xué)中的應(yīng)用研究*

廣州市白云區(qū)三元里中學(xué)(501400) 肖樂(lè)

思維導(dǎo)圖在初中幾何教學(xué)中的應(yīng)用研究*

廣州市白云區(qū)三元里中學(xué)(501400) 肖樂(lè)

“長(zhǎng)期以來(lái),中學(xué)生數(shù)學(xué)能力發(fā)展水平的一個(gè)關(guān)鍵的轉(zhuǎn)折點(diǎn),或者說(shuō)是劃分學(xué)生是否具有數(shù)學(xué)天賦的一個(gè)分水嶺,就是初中的平面幾何教學(xué).”[1]在2011版課標(biāo)提出的核心概念中,以幾何為載體的就有空間觀念、幾何直觀、推理能力等.平面幾何可以讓學(xué)生在學(xué)習(xí)過(guò)程中領(lǐng)悟到嚴(yán)謹(jǐn)?shù)倪壿嬐评砼c證明的思維方式,最能發(fā)展學(xué)生智能,提高學(xué)生思維素質(zhì),是其他任何學(xué)科難以企及的.人們通過(guò)這種學(xué)習(xí)可以認(rèn)識(shí)豐富多彩的圖形,建立與發(fā)展空間觀念,培養(yǎng)運(yùn)用幾何知識(shí)認(rèn)識(shí)世界與改造世界的能力.[2]可見(jiàn),幾何在研究、學(xué)習(xí)數(shù)學(xué)中是非常重要的,它也可以看做是最基本的能力.

但這么重要的內(nèi)容,卻讓學(xué)生的學(xué)和教師的教都感到力不從心.其原因在于平面幾何高度的抽象性,推理的嚴(yán)謹(jǐn)性、結(jié)論的明確性,以及大量定理、符號(hào)的理解應(yīng)用.再加上初中生缺乏空間想象能力,缺乏相應(yīng)的幾何知識(shí),缺乏邏輯推理能力,讓“學(xué)生的情感體驗(yàn)不好”導(dǎo)致產(chǎn)生幾何學(xué)習(xí)挫折感.

另外,許多教師的傳統(tǒng)教學(xué)觀念難以轉(zhuǎn)變,不能完全落實(shí)新課標(biāo)中“以學(xué)生為主體”的要求,在教學(xué)中仍然以教師講授為主.重記憶輕思維,重技巧輕方法,重灌輸輕啟發(fā)的現(xiàn)狀仍然存在,學(xué)生的合作、創(chuàng)新意識(shí)薄弱,幾何學(xué)習(xí)只是一味地做題,學(xué)生分?jǐn)?shù)提高了能力卻沒(méi)有提高.幾何課忽視學(xué)生發(fā)散思維、形象空間感和創(chuàng)新思維的培養(yǎng),同時(shí)還造成部分同學(xué)對(duì)數(shù)學(xué)失去興趣.

如何尋找一種有效的方法,在幾何教學(xué)中構(gòu)建培養(yǎng)學(xué)生思維能力的平臺(tái),使得教學(xué)富有生命力,讓幾何教與學(xué)的活動(dòng)成為一個(gè)主動(dòng)、自由且富有個(gè)性的智慧開(kāi)發(fā)過(guò)程?思維導(dǎo)圖教學(xué)為我們提供了一個(gè)這樣的機(jī)會(huì).那么,思維導(dǎo)圖究竟是什么?它有哪些重要的教學(xué)價(jià)值?如何在幾何教學(xué)中應(yīng)用思維導(dǎo)圖?在教學(xué)的不同階段開(kāi)展思維導(dǎo)圖教學(xué)的策略又有哪些?如何運(yùn)用思維導(dǎo)圖進(jìn)行題目分析?本文將對(duì)此進(jìn)行研究,期待找到有效的教學(xué)方法,提高學(xué)生數(shù)學(xué)能力,優(yōu)化課堂教學(xué).

一、思維導(dǎo)圖的概念

英國(guó)心理學(xué)家、腦力開(kāi)發(fā)專(zhuān)家東尼.博贊先生,于上世紀(jì)60年代提出思維導(dǎo)圖這一有效使用大腦的思考方法.思維導(dǎo)圖以腦神經(jīng)生理學(xué)習(xí)為基礎(chǔ)、多感官學(xué)習(xí)為特性,集文字、色彩、圖像等多種形式為一體,多維度表征知識(shí)和認(rèn)知結(jié)構(gòu).[3]思維導(dǎo)圖呈現(xiàn)的是一個(gè)思維過(guò)程,它往往從中心主題開(kāi)始,隨著思維的不斷深入,逐步形成一個(gè)向周?chē)l(fā)散而有序的樹(shù)狀圖,同一層節(jié)點(diǎn)數(shù)表示思維的廣度,一個(gè)分支的長(zhǎng)度表示思維的深度.如圖1,思維導(dǎo)圖結(jié)構(gòu)圖.

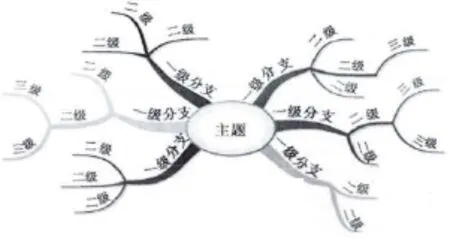
圖1 思維導(dǎo)圖結(jié)構(gòu)圖

二、思維導(dǎo)圖的類(lèi)別

思維導(dǎo)圖作為一種思維的可視化工具,能夠在一定程度上呈現(xiàn)一個(gè)人的思維過(guò)程,現(xiàn)已被廣泛應(yīng)用于教學(xué)的各個(gè)方面.根據(jù)構(gòu)圖主體的不同,有教師圖、學(xué)生圖、個(gè)體圖、小組圖和群體圖;根據(jù)課堂教學(xué)時(shí)間先后不同,可以有教學(xué)前圖、教學(xué)中圖和教學(xué)后圖;依據(jù)學(xué)習(xí)目的不同,可以有預(yù)習(xí)圖、筆記圖、復(fù)習(xí)圖和作業(yè)圖;根據(jù)繪圖復(fù)雜程度的不同,可以有簡(jiǎn)單圖和復(fù)雜圖;根據(jù)創(chuàng)作方式的不同,可以有手繪圖和軟件圖.[2]圖2為軟件繪圖,圖3為學(xué)生手繪圖.

圖2 軟件繪圖

圖3 學(xué)生手繪圖

三、思維導(dǎo)圖教學(xué)的意義

(一)思維導(dǎo)圖教學(xué)有利于促進(jìn)課改和新課標(biāo)的落實(shí)

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2011年版)》中提出:數(shù)學(xué)教學(xué)活動(dòng),特別是課堂教學(xué)應(yīng)激發(fā)學(xué)生興趣,調(diào)動(dòng)學(xué)生積極性,引發(fā)學(xué)生的數(shù)學(xué)思考,鼓勵(lì)學(xué)生的創(chuàng)造性思維;要注重培養(yǎng)學(xué)生良好的數(shù)學(xué)學(xué)習(xí)習(xí)慣,使學(xué)生掌握恰當(dāng)?shù)臄?shù)學(xué)學(xué)習(xí)方法.[2]新課標(biāo)還要求教師以學(xué)生為主體,注重教學(xué)過(guò)程中培養(yǎng)學(xué)生的能力,評(píng)價(jià)要關(guān)注學(xué)生學(xué)習(xí)的過(guò)程重于結(jié)果.思維導(dǎo)圖的特點(diǎn)遵循和體現(xiàn)了新課標(biāo)的理念及要求,在提高學(xué)生學(xué)科成績(jī)、激發(fā)學(xué)習(xí)動(dòng)機(jī)、提高問(wèn)題解決能力、促進(jìn)知識(shí)建構(gòu)和認(rèn)知發(fā)展等方面成效顯著,是提高學(xué)生數(shù)學(xué)綜合素質(zhì)的有效途徑.

(二)思維導(dǎo)圖教學(xué)有利于激發(fā)學(xué)生學(xué)習(xí)興趣,提高學(xué)生數(shù)學(xué)能力

思維導(dǎo)圖的創(chuàng)作過(guò)程就是學(xué)生提煉知識(shí)、分析問(wèn)題、解決問(wèn)題的過(guò)程,學(xué)生通過(guò)思維導(dǎo)圖整合知識(shí),構(gòu)建知識(shí)網(wǎng)絡(luò),濃縮知識(shí)結(jié)構(gòu),從整體上把握知識(shí).另外,思維導(dǎo)圖使抽象知識(shí)概念變得可視化,方便了對(duì)所學(xué)知識(shí)的加工,每個(gè)學(xué)生都可以創(chuàng)作出有個(gè)人風(fēng)格的作品,激發(fā)了學(xué)生的學(xué)習(xí)興趣,同時(shí)也提高了學(xué)生的數(shù)學(xué)能力.

(三)思維導(dǎo)圖教學(xué)有利于教師優(yōu)化教學(xué),促進(jìn)教師專(zhuān)業(yè)發(fā)展

思維導(dǎo)圖在教學(xué)領(lǐng)域中應(yīng)用,不僅可為學(xué)生所用,也可為教師所用,實(shí)現(xiàn)教學(xué)的統(tǒng)一性,也利于師生之間的交流和溝通.教師可以在教學(xué)設(shè)計(jì)、教學(xué)安排(課前預(yù)習(xí),課堂研習(xí),課后復(fù)習(xí))、不同課型(概念課、復(fù)習(xí)課)、題目分析中使用思維導(dǎo)圖,使教師適應(yīng)課改后的教學(xué)需要,促進(jìn)教師的專(zhuān)業(yè)發(fā)展,優(yōu)化課堂教學(xué).

四、思維導(dǎo)圖在幾何教學(xué)中的應(yīng)用

下面就以八年級(jí)四邊形內(nèi)容為例,說(shuō)明思維導(dǎo)圖的使用方法.

(一)思維導(dǎo)圖用于教學(xué)設(shè)計(jì)

教學(xué)設(shè)計(jì)是教師對(duì)教學(xué)活動(dòng)所進(jìn)行的設(shè)計(jì),思維導(dǎo)圖為教師提供了一種新的教學(xué)設(shè)計(jì)思路.它以清晰的結(jié)構(gòu)展現(xiàn)各概念、知識(shí)點(diǎn)之間的邏輯關(guān)系,明確教學(xué)重、難點(diǎn),并對(duì)各種教學(xué)觀點(diǎn)和經(jīng)驗(yàn)加以分類(lèi)、組合和整理.如圖4,平行四邊形性質(zhì)第一課的教學(xué)設(shè)計(jì)圖

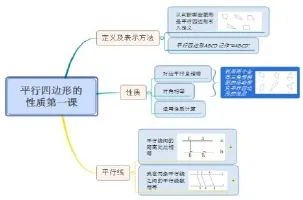
圖4 平行四邊形的性質(zhì)第一課教學(xué)設(shè)計(jì)圖

其中“平行四邊形的性質(zhì)第一課”為主題,三個(gè)一級(jí)分支分別為:“定義及表示方法”、“性質(zhì)”、“平行線”,在每個(gè)一級(jí)分支下出現(xiàn)二級(jí)分支……相較于傳統(tǒng)的教學(xué)設(shè)計(jì),思維導(dǎo)圖能夠?qū)㈦[藏于教師頭腦中的教學(xué)內(nèi)容、教學(xué)思路、教學(xué)經(jīng)驗(yàn)和知識(shí)體系以一種可視化的方式展現(xiàn)出來(lái),相當(dāng)于模擬了一次教學(xué)過(guò)程.

(二)思維導(dǎo)圖用于教學(xué)過(guò)程

1.思維導(dǎo)圖運(yùn)用于幾何概念課

學(xué)生在學(xué)習(xí)新的概念之前,往往會(huì)忘記舊的概念.教師可先將學(xué)生頭腦中已有的幾何概念體系,以思維導(dǎo)圖的形式呈現(xiàn)出來(lái),再不斷將新的幾何概念添加到現(xiàn)有的導(dǎo)圖中,知識(shí)體系也會(huì)隨之不斷擴(kuò)大和豐富.

教師可以從以下幾個(gè)環(huán)節(jié)將思維導(dǎo)圖應(yīng)用于幾何概念課:

(1)利用導(dǎo)圖復(fù)習(xí)舊概念

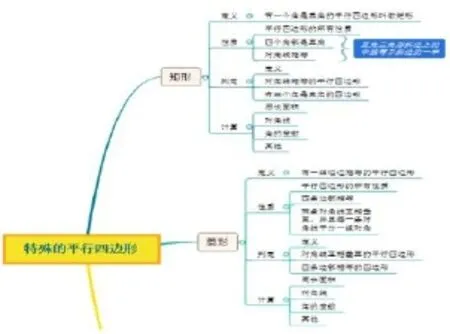
圖5 特殊的平行四邊形舊知圖

掌握舊知是學(xué)習(xí)新知的前提,在新課導(dǎo)入前,教師和學(xué)生可以在黑板上共同展示上節(jié)課內(nèi)容的思維導(dǎo)圖(可以是手繪圖也可以是軟件繪圖),對(duì)舊概念進(jìn)行復(fù)習(xí)回顧.八年級(jí)學(xué)生已經(jīng)學(xué)習(xí)了矩形和菱形這兩種特殊的平行四邊形,導(dǎo)入新課正方形前,可以先對(duì)這種圖形進(jìn)行復(fù)習(xí).如圖5,特殊的平行四邊形舊知圖.其中,“矩形”、“菱形”的定義、性質(zhì)、判定、計(jì)算為二級(jí)分支.

(2)在導(dǎo)圖中引入新概念

復(fù)習(xí)完舊概念后,可以將“正方形”作為新的一級(jí)分支添加到舊的導(dǎo)圖上.對(duì)比之前的探究?jī)?nèi)容,如“概念、性質(zhì)、判定和計(jì)算等”,引導(dǎo)學(xué)生自主探究學(xué)習(xí),添加三級(jí)分支.本環(huán)節(jié)的思維導(dǎo)圖模板如圖6所示.

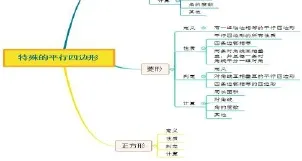
圖6 特殊的平行四邊形舊知圖(1)

用思維導(dǎo)圖這種教學(xué)手段,有利于將零散的幾何概念整合起來(lái),更有助于學(xué)生清楚地認(rèn)識(shí)到新、舊幾何概念之間的邏輯關(guān)系.

(3)建構(gòu)和完善導(dǎo)圖中的新概念

此環(huán)節(jié)師生可重點(diǎn)討論判定.由于課本沒(méi)有直接給出正方形判定的定理,對(duì)此學(xué)生的聯(lián)想非常豐富.有學(xué)生從正方形的定義得出四條邊都相等,四個(gè)角都是直角的四邊形是正方形,也有同學(xué)認(rèn)為要先證明出矩形或者菱形,再得出正方形.教師可以將學(xué)生提出的判定一一羅列出來(lái),讓學(xué)生進(jìn)行小組討論.師生對(duì)討論結(jié)果進(jìn)行分類(lèi)和組織,最后共同繪制出正方形判定的三級(jí)分支,并統(tǒng)一了正方形的常用證法,即先證明是矩形或者菱形,再添加邊、角或?qū)蔷€條件,證明正方形.本環(huán)節(jié)的導(dǎo)圖如圖7所示.

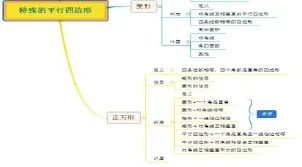
圖7 特殊的平行四邊形舊知圖(2)

在教學(xué)過(guò)程中,要注意激發(fā)和拓展學(xué)生思維.對(duì)于學(xué)生的回答和解釋,甚至是想象和假設(shè),教師需要給予足夠重視,并給予適當(dāng)講解和啟發(fā).教師及時(shí)總結(jié),并再次給予提升和點(diǎn)撥.在問(wèn)題提出、解答,不斷追問(wèn)、不斷明朗的過(guò)程中,學(xué)生經(jīng)歷了完整的思維過(guò)程.[2]

(4)用導(dǎo)圖總結(jié)歸納單元知識(shí)

在完成四邊形單元的學(xué)習(xí)后,教師可以要求學(xué)生獨(dú)立繪制整章的思維導(dǎo)圖,便于學(xué)生加深對(duì)本章幾何知識(shí)的理解,把握整體概念.同時(shí)可評(píng)選出優(yōu)秀的思維導(dǎo)圖作品進(jìn)行展覽,提高學(xué)生對(duì)幾何學(xué)習(xí)的興趣和積極性.如圖8,學(xué)生手繪的四邊形思維導(dǎo)圖.

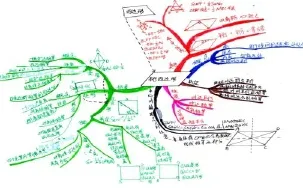
圖8 學(xué)生手繪的四邊形思維導(dǎo)圖

思維導(dǎo)圖應(yīng)用于幾何教學(xué)中,學(xué)生依賴于原有的認(rèn)知經(jīng)驗(yàn)和當(dāng)前的學(xué)習(xí)情境,在頭腦中綜合考慮各種信息,并對(duì)其梳理、分析和組織,創(chuàng)建知識(shí)網(wǎng)絡(luò),有利于培養(yǎng)學(xué)生的數(shù)學(xué)能力和創(chuàng)新思維.

2.思維導(dǎo)圖運(yùn)用于幾何題目分析

對(duì)初中生來(lái)說(shuō),學(xué)生幾何概念知識(shí)較為薄弱,抽象思維的形成也處于初步階段,面對(duì)復(fù)雜的幾何問(wèn)題常常束手無(wú)策.將思維導(dǎo)圖引入到幾何題目的分析中,可以幫助學(xué)生整理思路,將問(wèn)題與有關(guān)概念、定理聯(lián)系起來(lái),對(duì)條件、概念、定理進(jìn)行整合梳理,最終找到解題方法.下面以2014年寧波的一道數(shù)學(xué)中考題為例,說(shuō)明思維導(dǎo)圖如何應(yīng)用于幾何問(wèn)題分析.

如圖,正方形ABCD和正方形CEFG中,點(diǎn)D在CG上,BC=1,CE=3,H是AF的中點(diǎn),那么CH的長(zhǎng)是( )

圖9

分析過(guò)程有三步:1.對(duì)題目所提供的條件進(jìn)行聯(lián)想、提煉,從而找出問(wèn)題的關(guān)鍵點(diǎn);2.從關(guān)鍵點(diǎn)出發(fā),產(chǎn)生聯(lián)想,找出所有與關(guān)鍵點(diǎn)相關(guān)的幾何知識(shí);3.判斷,就是根據(jù)聯(lián)想出的知識(shí)點(diǎn)判斷哪些可以為我們所用.如圖9,中考題分析思維導(dǎo)圖

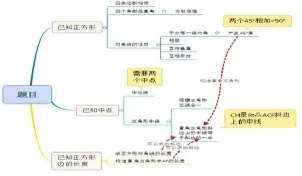
圖10 中考題分析思維導(dǎo)圖

具體來(lái)說(shuō)就是,首先從題目中聯(lián)想概括出關(guān)鍵點(diǎn)“正方形、中點(diǎn)、正方形邊的長(zhǎng)度”,即導(dǎo)圖的一級(jí)分支;其次,從每個(gè)關(guān)鍵點(diǎn)聯(lián)想出若干相關(guān)知識(shí),即導(dǎo)圖的二級(jí)分支,再?gòu)亩?jí)分支聯(lián)想出三級(jí)分支,一直聯(lián)想下去…….此題從正方形的性質(zhì)中聯(lián)想到,對(duì)角線平分每一組對(duì)角得到45°角,因此兩個(gè)正方形就有了45°+45°=90°;最后,通過(guò)導(dǎo)圖各個(gè)分支末端展示的知識(shí)點(diǎn),尋找它們之間的聯(lián)系,判斷使用那些知識(shí)點(diǎn).我們發(fā)現(xiàn)通過(guò)兩個(gè)45°可以構(gòu)造出直角三角形,通過(guò)正方形的邊長(zhǎng)或者對(duì)角線長(zhǎng)都可以求出△ACF的斜邊,最終通過(guò)“直角三角形斜邊上的中線是斜邊的一半”定理求出CH的長(zhǎng)度.

解答過(guò)程:如圖,連接AC、CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,∵H是 AF的中點(diǎn),∴.故選:B.

幾何知識(shí)點(diǎn)多而雜,運(yùn)用思維導(dǎo)圖這個(gè)工具進(jìn)行梳理,使得思維過(guò)程條理化、可視化,極大地提高了解題效率.學(xué)生只需要努力掌握好基礎(chǔ)知識(shí),從題目的條件出發(fā),就能一步一步找到問(wèn)題的答案.

3.思維導(dǎo)圖運(yùn)用于教學(xué)評(píng)價(jià)

由于學(xué)生存在理解能力、認(rèn)知水平等方面的差異,在理解概念、建構(gòu)知識(shí)網(wǎng)絡(luò)存在一定的困難.因此在課堂學(xué)習(xí)中,展現(xiàn)并評(píng)價(jià)學(xué)生先前的知識(shí)和經(jīng)驗(yàn),從而進(jìn)行有針對(duì)性的教學(xué)顯得尤為重要.思維導(dǎo)圖可以有效呈現(xiàn)并評(píng)價(jià)學(xué)生的知識(shí)結(jié)構(gòu),課前,它可以幫助學(xué)生識(shí)別各部分知識(shí)之間的關(guān)系,診斷學(xué)生對(duì)舊知識(shí)的理解;課中,它還可以幫助師生了解學(xué)習(xí)的進(jìn)展和思維的過(guò)程,確認(rèn)知識(shí)的掌握程度;課后,它還可以輔助學(xué)生回顧、總結(jié)和復(fù)習(xí)所學(xué)內(nèi)容,檢驗(yàn)學(xué)生的整體理解和系統(tǒng)掌握.思維導(dǎo)圖不僅評(píng)價(jià)思維的結(jié)果,更注重思維的過(guò)程.總之,在幾何課中開(kāi)展思維導(dǎo)圖的教學(xué)評(píng)價(jià),不僅為學(xué)生開(kāi)辟了一個(gè)相互學(xué)習(xí)與交流、共同提高與發(fā)展的學(xué)習(xí)平臺(tái),而且凸顯“情感、態(tài)度與價(jià)值觀”的培養(yǎng),促進(jìn)學(xué)生能力的發(fā)展和數(shù)學(xué)素養(yǎng)的提高.[2]

五、總結(jié)與展望

思維導(dǎo)圖應(yīng)用于幾何教學(xué),是一種全新的教學(xué)模式.它以教學(xué)核心問(wèn)題為主線,將整個(gè)教學(xué)看做完整的動(dòng)態(tài)開(kāi)放系統(tǒng),呈現(xiàn)教學(xué)內(nèi)容步步深入、目標(biāo)漸漸達(dá)成的教學(xué)過(guò)程.思維導(dǎo)圖以圖示的方式將分散的知識(shí)點(diǎn)系統(tǒng)整合,有效呈現(xiàn),代替?zhèn)鹘y(tǒng)的枯燥文字說(shuō)明,以更加直觀的形式呈現(xiàn)在學(xué)生面前,在開(kāi)發(fā)學(xué)生的智力、培養(yǎng)學(xué)生的思維能力、調(diào)動(dòng)學(xué)生學(xué)習(xí)的積極性,優(yōu)化課堂教學(xué)方面發(fā)揮著重要的作用.

筆者在自己所執(zhí)教的兩個(gè)平行班中的一個(gè)開(kāi)展了一個(gè)學(xué)期左右的思維導(dǎo)圖教學(xué).與普通教學(xué)班相比,應(yīng)用思維導(dǎo)圖的教學(xué)班學(xué)生的學(xué)習(xí)興趣和成績(jī)得到了顯著提高,對(duì)于班里中等生的影響效果尤其明顯,學(xué)生們希望教師繼續(xù)開(kāi)展思維導(dǎo)圖教學(xué).

在一個(gè)良好的開(kāi)端后,我們將繼續(xù)思考、探索、研究:思維導(dǎo)圖教學(xué)如何運(yùn)用于“課題型”課堂教學(xué)?長(zhǎng)期開(kāi)展思維導(dǎo)圖教學(xué)后,會(huì)給學(xué)生帶來(lái)怎樣的思維提升?此教學(xué)模式推廣到其他班級(jí)和其他學(xué)科又將如何等問(wèn)題,讓這一思維模式更多地造福教育,讓更多地學(xué)生終身受益.

[1]朱文芳、周志英.初中數(shù)學(xué)[M].上海:華東師范大學(xué)出版社,2008.103.

[2]董博清.基于思維導(dǎo)圖的中學(xué)物理教學(xué)實(shí)證研究[D]:[博士學(xué)位論文].長(zhǎng)春:東北師范大學(xué),2013.5.

[3]東尼·博贊.思維導(dǎo)圖[M].北京:中信出版社,2009.4-7.

[4]中華人民共和國(guó)教育部.全日制義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2011年版)[S].北京:人民教育出版社,2011.

[5]義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)解讀:2011年版[S].北京:北京師范大學(xué)出版社,2012.2.

[6]盧沉.關(guān)于初二學(xué)生在幾何證明中認(rèn)知錯(cuò)誤分析及教學(xué)對(duì)策研究[D]:[碩士學(xué)位論文].上海:師范大學(xué),2011.4.

[7]張紅艷.思維導(dǎo)圖在初中幾何概念教學(xué)中的應(yīng)用研究[D]:[碩士學(xué)位論文].天津:天津師范大學(xué),2014.3.

[8]張奠宙.平面幾何教學(xué)的回顧與前瞻.數(shù)學(xué)教學(xué)[J].2005,(5):2.

[9]李曉鵬.中學(xué)生思維導(dǎo)圖學(xué)習(xí)法[M].北京:光明日?qǐng)?bào)出版社,2014.6

*本文為廣州市教育科學(xué)“十二五”規(guī)劃課題:問(wèn)題驅(qū)動(dòng)教學(xué)模式下的初中數(shù)學(xué)概念課、規(guī)則課與命題課教學(xué)研究(立項(xiàng)號(hào):120153761)研究成果.