錯在哪兒?—由一道中考錯題想到的

北京師范大學出版集團(100875) 岳昌慶

錯在哪兒?—由一道中考錯題想到的

北京師范大學出版集團(100875) 岳昌慶

存在性問題一直是各級各類考試命題的重中之重的問題,能舉出反例更是至關重要的,尤其是中考、高考等高利害性考試.請看2015年中考某市選擇題的壓軸題

例 1 已知拋物線 y=ax2+bx+c(a＞ 0)過(?2,0),(2,3)兩點,那么拋物線的對稱軸( ).

A.只能是x=?1

B.可能是y軸C.在y軸右側且在直線x=2的左側

D.在y軸左側且在直線x=?2的右側

由于第一大題(選擇題)中明確指出“在每小題給出的四個選項中,只有一項是符合題目要求的”故選D.

錯解2:因為函數圖像經過(?2,0),(2,3)兩點,所以由二次函數圖像的對稱性可知:函數圖像與x軸的另一個交點在點(2,0)的左側,所以拋物線的對稱軸在y軸的左側且在直線x=?2的右側.故選D.

錯因分析:錯解1排除法不靠譜,默認前提:有且只有一個答案正確!

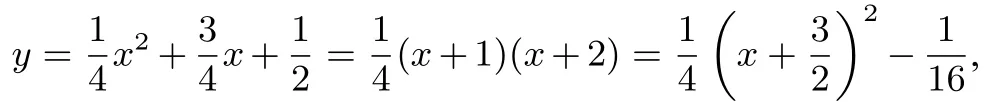
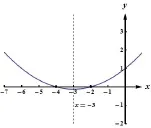
圖1

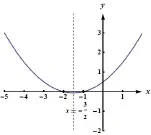
圖2

相信當時此題對考生影響不是太大,錯解1及錯解2均可“正確”選出答案D.可能心細的學生在此題上會多花一些時間,吃虧一些,略欠公允.

如何回避類似情況,以規避風險?

本著以人為本對考生負責的態度,建議中考命題專家組中,既要有初中一線教師、教研員,也要有高中一線教師、教研員,更要有大學教師把關.命題、審題、打印、校對、驗算、保密等均是不可缺少的環節,甚至不排除小范圍請教師、各級各類有代表性的學生試做.用《幾何畫板》驗證其存在性、正確性等,切忌信手拈來、想當然.不能讓崇高神圣的命題工作成為一種“意識流”.

另:各地教研機構、雜志、網絡等勇于挑錯、勇于正視瑕疵,將中考數學試題中的瑕疵曝于陽光下,以免一錯再錯,以訛傳訛,繼續貽誤學子,損害高利害性考試的權威性與公信力.

例2[2015年中考四川省廣元市卷第23題9分次壓軸題][2012年中考湖北省恩施州卷第23題12分]如圖,AB是⊙O的弦,D為半徑OA的中點,過D作CD⊥OA交弦于點E,交⊙O于點F,且CE=CB.

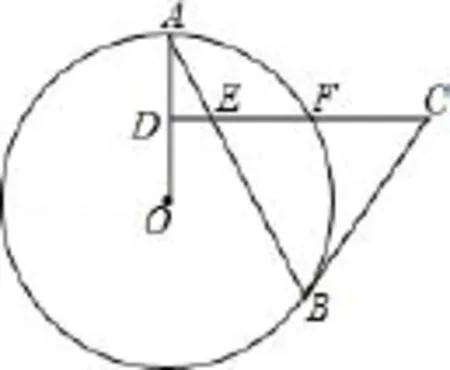
圖2

(1)求證:BC是⊙O的切線;

(2)連接AF,BF,求∠ABF的度數;

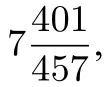
評注 一個錯題不斷流傳之廣,還能在3年后,又原封不動地作為另一個地區的中考壓軸題.

例3[2015年中考廣西南寧市卷第11題3分次壓軸題]如圖,AB是⊙O的直徑,AB=8,點M在⊙O上,∠MAB=20°,N是弧MB的中點,P是直徑AB上一動點,若MN=1,則△PMN周長的最小值為( ).

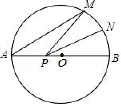
圖4

A.4 B.5 C.6 D.7

所謂標準答案為B.

錯因分析:“MN=1”是個富裕條件,且是個錯誤條件.實際上,考生可以算出MN=8sin10°≈8×0.1736≈1.39＞1,A.B.C.D.依次改為A.3+8sin10°,B.4+8sin10°,C.5+8sin10°,D.6+8sin10°.

例4[2014年中考四川省遂寧市卷第9題4分]如圖,AD是△ABC中∠BAC的角平分線,DE⊥AB于點E,S△ABC=7,DE=2,AB=4,則AC長是( )

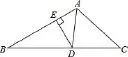
圖5

A.3 B.4 C.6 D.5

所謂標準答案為A.

錯因分析:若“AC=3”,過D作DF⊥AC于F,顯然Rt△AEDRt△AFD,DF=DE=2,設AE=AF=x,則BE=4?x,CF =3?x,由角平分線定理得即7x2?24x+28=0,此方程無解.即符合已知條件的圖是不存在的.

例 5[2014年中考湖北省隨州市卷第9題3分]在等邊△ABC中,D是邊AC上一點,連接BD,將△BCD繞點B逆時針旋轉60°,得到△BAE,連接ED,若BC=5,BD=4.則下列結論錯誤的是( ).

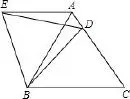
圖6

A.AE//BC B.∠ADE=∠BDC

C.△BDE是等邊三角形 D.△ADE的周長是9

所謂標準答案為B.

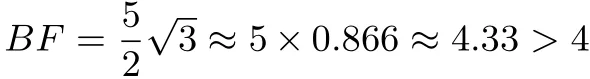
例6[2014年中考湖北荊門卷第6題3分]如圖,AB是半圓O的直徑,D,E是半圓上任意兩點,連結AD,DE,AE與BD相交于點C,要使△ADC與△ABD相似,可以添加一個條件.下列添加的條件其中錯誤的是( ).

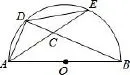
圖7

A.∠ACD=∠DAB B.AD=DE

C.AD2=BD·CD D.AD·AB=AC·BD

所謂標準答案為D.

錯因分析: 實際上A.B.C.D.全部正確,沒有錯誤答案.可能是校對環節出了問題,只需將選項D中的“AD”改為“CD”即可.