分析法在數學教學中的運用*

廣州市增城區增城中學(511300) 鄭春立

分析法在數學教學中的運用*

廣州市增城區增城中學(511300) 鄭春立

分析法在解題過程中溯本求源,啟發思維,梳理思路,突破難點,有著很好的引導作用;在分析題目的過程中,也能提高對知識的認識.在教學過程中,滲透分析教學,引導學生學會思考是很有必要的.以下是筆者在教學過程中的幾點體會,以饗讀者.

一、分析法在梳理思路,溯本求源的運用

立體幾何考查學生空間幾何想象能力,以及數量關系.對部分女生而言,“垂直”關系是“剪不斷,理還亂”的問題.分析法,在立體幾何的證明中,起著梳理思路,溯本求源的引導作用.

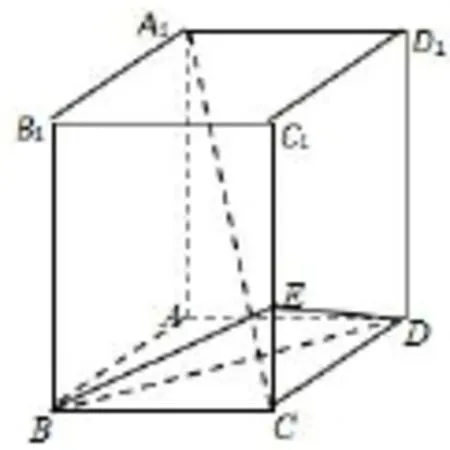
圖1

(I)求三棱錐C?BED的體積;

(II)求證:A1C⊥平面BDE.

分析:(I)略

(II)有學生由平面AA1C⊥平面BDE推導A1C⊥平面BDE的錯誤.一方面學生對面面垂直推線面垂直的必要不充分條件的不理解;另一方面是對線面垂直與線線垂直轉化的混亂.如果采用分析法,則思路就清晰許多:

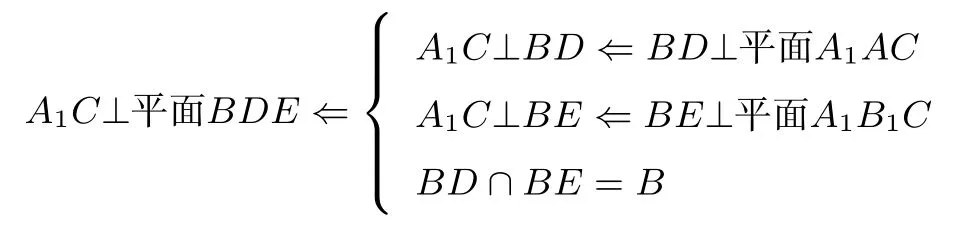
其他解法略.由此可見在立體幾何中,對于關系較為復雜的題目,用分析法追尋條件,整理思路,再用綜合法條理書寫是很有必要的.

二、分析法在化解抽象,突破難點的運用

必修三的算法案例,本意應該是體現算法運用,突出算法解決問題的思路.但是案例解題原理相對一部分學生而言,存在很大的理解障礙.如果在算法案例中,采用分析法分析算法.可以起到化解抽象,突破難點的運用.如輾轉相除法求最大公約數的案例分析.如果按原理分析則比較嚴謹、但字母繁雜比較抽象.有些老師采用講解的辦法:如果除數與余數有公因數,那么這個被除數也有這個公因數,即除數與余數的公因數和被除數與除數的公因數相同.所以,輾轉相除直至整除為止,即求最大公約數.這種分析,比原理分析簡易許多,學生也較易接受.而筆者認為如果從實例出發,引導學生“倒敘”分析更易理解:由于輾轉相除法最后一步被除數整除除數,即上一步除數與余數有公約數,由此,該公約數也是被除數與除數的公約數.而為何是“最大公約數”?能整除余數的最大約數也就是它本身.這樣由具體例子分析原理題,引導學生回歸具體過程,由具體到抽象,更易化解抽象問題,突破教學難點.

三、分析法在啟迪思路、提高對知識認識的運用

應用題結合生活背景考查數學知識的應用,向來是學生比較薄弱且害怕的題型.分析法在如何提高學生的生活認識與知識的運用就有很好的引領作用.在《數列在日常經濟生活中的應用》一課,筆者先幫學生預習了單利、復利以及分期付款規定等相關的經濟知識,并加以例子解釋.然后再以生活中常見的分期付款問題進行探討.

例子:小華準備購買一臺售價為5000元的電腦,采用分期付款的方式,并在一年內將款全部付清.商場提出的付款方式為:購買后2個月第1次付款,再過2個月第2次付款……購買后12個月第6次付款,每次付款金額相同,約定月利率為0.8%,每月利息按復利計算.求小華每期付的金額是多少?

在探討過程中,引導學生往兩種思路分析.

思路1:考慮小華每次還款后,還欠商場的金額.

思路2:小華在12月中共付款6次,它們在12個月后的本利和的累加與一年后付款總額相等.

學生按思路1很快通過列舉找到等量關系,進而解決問題.但對于第二種思路,學生想不明,解釋又很難講透.我只好采用緩兵計暫時緩緩:方法2技巧性較強,但很難理解,如果不會可以用方法1,至于方法2,有興趣的同學課后再與老師討論.課后,學生甲詢問第2種解法,但按授課時的思路分析還是講不通.最后,我無奈地指第1種解法過程,引導她將解法1移項變形,問題能否將“購買一臺售價為5000元的電腦”理解成“一次性存款5000元一年”,“分6次付款金額相同”是否相當于“6次分期等額存款”,“分期還清”是否等價于“一次性存款跟分期存款到年末的本利和相等”.令人驚喜的是:學生結合解法1的結果竟然很容易就理解了解法2.原來有時從答案出發,“倒敘”求解竟然是突破難點的一種捷徑!

教學中的“教”是為了“不教”,在平時的教學中滲透分析教學,引導學生學會思考是很有必要的.

[1]普通高中課程標準實驗教科書數學必修3[S].人民教育出版社.2013.

[2]郭秀玲.李忠海.學生數學問題表征能力分析[J],中學數學教與學,2009,(2)

*本文系廣東省教育研究院2015年度課題“‘問題導學’模式下學生學習方式轉變的教學策略研究”(課題編號:GDJY-2015-A-b057)的階段性研究成果之一.