從高三講評課看變式教學對提升學生數(shù)學反思能力的作用
廣東廣雅中學(510160) 溫麗
從高三講評課看變式教學對提升學生數(shù)學反思能力的作用
廣東廣雅中學(510160) 溫麗
當今科技與信息快速發(fā)展的大環(huán)境對我國的高中數(shù)學教學提出了更高的要求,不僅需要注重知識的傳授,而且更重的是要教會學生要會學數(shù)學和會用數(shù)學,在教學活動中培養(yǎng)學生的創(chuàng)新精神和創(chuàng)造能力.長期以來,在“應試教育”的口號下,“掐頭去尾抓中段”的“題海戰(zhàn)術(shù)”嚴重困擾著我國的中學教學,導致好多學生討厭數(shù)學,是限制學生在教學活動中的積極性、主動性和創(chuàng)造性的主要根源.因此,現(xiàn)階段我國的中學數(shù)學教學實踐研究和改革的關(guān)鍵是探索比較有效的教學策略和教學方法,采用一種比較適合中國學生的課堂教學模式,在此背景下,變式教學及其模式就應運而生,是達到學生在教學活動中發(fā)揮其積極性、主動性和創(chuàng)造性這一目的的一個非常有效的途徑.
一、變式教學的應遵循的原則
變式就是通過對原有問題的非本質(zhì)屬性的變換,而保持本質(zhì)屬性不變,說到底變式教學也只是教學的一種方式,其根本目的都是幫助學生更好的掌握和吸收已學的知識,如果僅是一味的為變而變,這樣就偏離了最根本的教學目標,因此,筆者認為變式教學應遵循目的性,反思性和主動性三大原則.
所謂目的性指在進行變式教學時要緊扣教學目標,弄清楚哪些問題要變,為什么要變,不能為變而變,避免隨意變式教學.
所謂反思性指對過去事情的重新思考,并從中總結(jié)經(jīng)驗教訓.數(shù)學的學習要經(jīng)常進行反思,有反思才能發(fā)現(xiàn)問題,有反思才能促進思維發(fā)展,有反思才能不斷進步.
所謂主動性指教師要積極啟發(fā)引導學生充分調(diào)動認知結(jié)構(gòu)中與新知識相聯(lián)系的舊知識以及(直接或間接)經(jīng)驗,讓學生主動的參與到構(gòu)造變式中,從而主動的去發(fā)現(xiàn)新知識的本質(zhì)屬性,以及構(gòu)建知識之間的聯(lián)系,加深對新舊知識的理解與內(nèi)化.
二、變式教學在高三講評課中的應用案例
隨著高三第一輪復習的深入很多學校都會采用“天天一小練,周周一大練,月月模擬練”的高強度的模擬考試復習方法.試卷講評課就成為高三數(shù)學復習的另一種常態(tài)課,試題的評析活動學生就成為學生知識、經(jīng)驗、能力增長的關(guān)鍵點.變式教學也就成為了講評課常用的方式,旨在幫助學生梳理相關(guān)知識點,從而找到問題的本質(zhì),挖掘解決問題的通法.下面就高三某次月考試卷的講評課具體闡述變式教學對提高學生反思能力的作用.
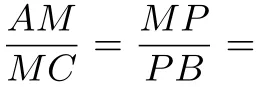

圖1
這類向量的問題在考試中經(jīng)常出現(xiàn),而向量又是學生的弱項之一,因此,很多學生一見到向量的問題就覺得找不到方向,不是做不對就是費了很多時間和精力才完成.其實,最根本的就是學生對向量基本定理的理解和使用還不到位,那么,如果不用向量基本定理就沒有方法可以解決了嗎?實則不然,具體解法如下:

從上述問題可知,利用向量解決問題基本上是幾何法和代數(shù)法,這是解決向量問題的兩個不同方向,幾何法的關(guān)鍵是找準基底,而我們常選澤已知模長和夾角的兩個向量作為基底;代數(shù)法的關(guān)鍵是合理建立坐標系,準確寫出相關(guān)點的坐標,而我們建系常遵循的原則就是使盡可能多的點在坐標軸上,并兼顧對稱性來建系.解題時只要找準大方向順藤摸瓜就可以了,課堂上作者給學生做了2016年天津卷和江蘇卷的兩道向量題,大部分學生還是比較快的得到了答案,課后有學生說上完這節(jié)課突然感覺知道了好多關(guān)于向量的“內(nèi)幕”,終于理清思路了.

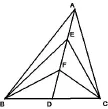
圖4
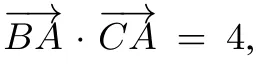

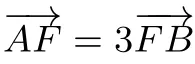

此題得分率也較低,學生反映感覺題目條件較多,比如利用拋物線的定義將到焦點的距離轉(zhuǎn)化為到準線的距離,又如焦點弦有好多相關(guān)的結(jié)論,不知從何入手,若是聯(lián)立直線方程與拋物線方程又覺得對于這樣的選擇題是否是太煩瑣了.其實,只要抓住問題的關(guān)鍵、把握問題的本質(zhì)就會有方向了,當然焦點弦的相關(guān)結(jié)論則是優(yōu)化和快速解決問題的工具.

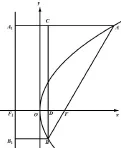
圖5

拋物線的焦點弦問題有很多特殊的性質(zhì),由解法1可以求出A,B兩點的坐標,也就是說直線AB是確定的,為了更好地理解本題可做如下變式:

變式2:若已知過拋物線y2=4x的焦點F的直線AB的斜率為,若,求滿足條件的λ的值.
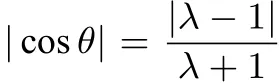

三、高三講評課實施變式教學提升反思能力的效果
變式教學作為我國傳統(tǒng)教學中的優(yōu)秀成分,近年來雖然已得到越來越多的理論支撐,但在實踐層面上,系統(tǒng)地探究如何借助變式教學提高課堂教學效率仍是一個很有價值的研究課題.而追問提高課堂教學效率的根本,即更好地實現(xiàn)教學目標,其中最基本的即為學生提供更多的積極思考的機會,這種思考既包括對數(shù)學對象的思考,也應包括對思考的思考,即反思,是一種元認知.綜上所述,運用變式教學來培養(yǎng)學生的數(shù)學反思能力既可改善學生缺少反思機會的現(xiàn)狀,又能增強變式教學的成效.因此,探討利用變式教學培養(yǎng)學生數(shù)學反思能力的策略是當下亟待開拓的一片“荒野”.變式教學正是為了彌補接受學習的不足,充分發(fā)揮學生主觀能動性,變被動學習為主動學習,進而達到提高學習效率之目的.高考數(shù)學命題積極倡導“加強創(chuàng)新意識的考查,實現(xiàn)選拔功能”,從各省市的考題分析來看,高考數(shù)學題往往“源于課本,高于課本”,在數(shù)學教學中注重變式的訓練,這是提升學生數(shù)學反思能力,提高數(shù)學學習效率,激發(fā)學生對數(shù)學學習的興趣和信心的重要途徑.
如今變式教學已經(jīng)成為高中數(shù)學教師上課時慣用的方式,而高三的試卷講評課則要求更高層次的變式,其主要呈現(xiàn)形式是通過一題多解、一題多變或是多題歸一的方式,引導學生學會思考和總結(jié),不斷反思,進而得到一些規(guī)律性的結(jié)論,對以后做題將大有裨益.隨著變式教學的不斷深入,學生由一開始依靠老師的引導去反思和總結(jié),逐漸變成學生能夠獨立反思,并且自主變換條件互相討論,經(jīng)常可以得到更多更細致的結(jié)論,從而加深對問題本質(zhì)的認識與理解,找到問題解決的規(guī)律和套路,實現(xiàn)融會貫通,觸類旁通的效果.由此可見,變式教學對提高學生的反思能力有很大的促進作用,借助數(shù)學變式教學提升反思能力是學生綜合素質(zhì)提升的重要途徑.值得好好推廣.
[1]吳小鋒.數(shù)學變式教學的作用與意義[J].數(shù)學教學研究,2009,6:25-27.
[2]鄭志培,潘菊玲.新課程背景下初高中數(shù)學教學現(xiàn)狀及其銜接對策[J].中學數(shù)學,2008,10:3-6
[3]劉瑞美.圓錐曲線焦點弦的一個性質(zhì)[J].中學數(shù)學教學參考,2009,10.
[4]張斌.談圓錐曲線焦點弦的一個性質(zhì)[J].中學數(shù)學,2010,3.
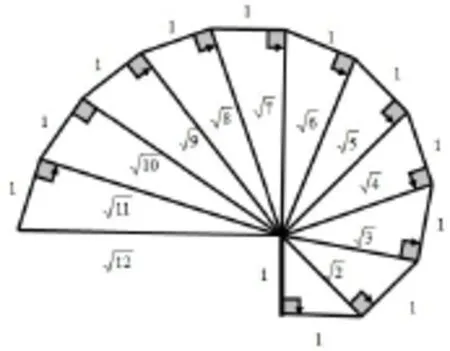
圖1
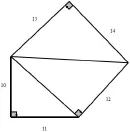
圖2
同樣可以用圖形證明命題的存在性.我們知道數(shù)軸的點有的表示有理數(shù),有的表示無理數(shù)利用勾股定理可以作出,···等線段.如圖1
在直角三角形中,利用勾股定理可以作出以下線段并且,滿足等式102+112+122=132+142,如圖2
同理等式212+222+232+242= 252+262+272,如圖3
圖3
等等這些圖形都表明命題的正確性.
總之,在自然數(shù)中有這么一組(2n+1)個的數(shù),符合條件、滿足連續(xù)自然數(shù)的平方和可用數(shù)形結(jié)合的階梯形式延伸而擴展.
參考文獻
[1]義務教育課程標準實驗教科書數(shù)學(八年級下冊)人民教育出版社,第64頁18·1勾股定理的章節(jié)

