討論形如abc=1的一類初中數學聯賽題
四川師大附屬第一實驗中學(610000) 董永春 陳剛
南充市儀隴縣瓦子鎮瓦子鎮小學校(637654) 車進明
討論形如abc=1的一類初中數學聯賽題
四川師大附屬第一實驗中學(610000) 董永春 陳剛
南充市儀隴縣瓦子鎮瓦子鎮小學校(637654) 車進明
筆者在近年的教學中發現形如abc=1或者a+b+c=1的代數式問題,由于形式優美,變換靈活,在初中數學聯賽及一些競賽中經常出現.筆者通過研究整理,總結了一些常用簡單方法,現舉例說明.
1.簡單單一分母通分型

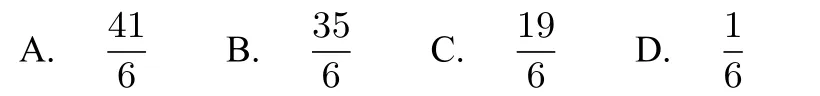
分析:結合已知條件,將分式通分,利用代數式恒等變形及整體代換來求值.通分后整體代換已知條件是關鍵.
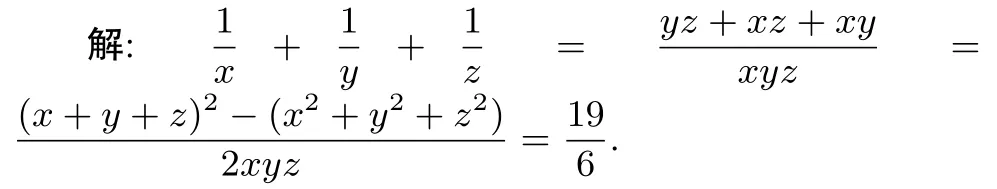

A.正數 B.0
C.負數 D.正、負不能確定
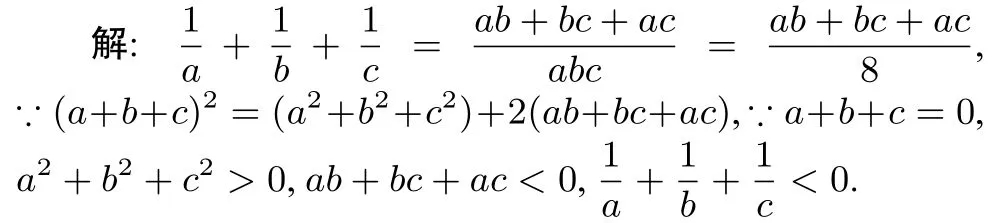
2.復雜分母因式分解型
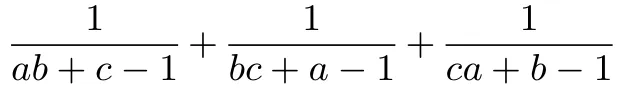
分析:分母形式復雜的不易通分,借助已知條件整體代換,將分母因式分解來求解.因式分解分母是關鍵.
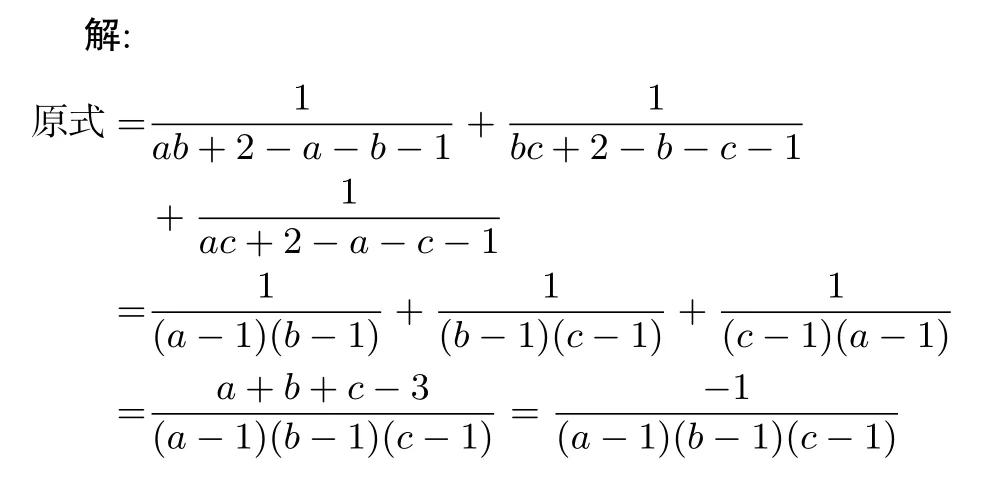


分析:首先分母通過已知條件整體代換來因式分解,然后復雜的分子因式分解比較困難時,初中常采用待定系數法來解決,此類分子分母都比較復雜的,在因式分解有困難時可以考慮待定系數法分解.


3.公式法
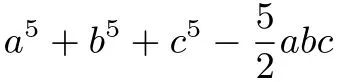
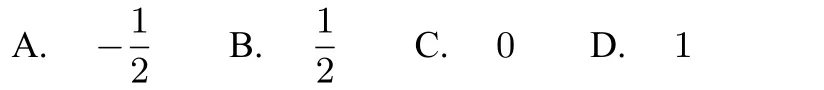
分析:對于這類高次的代數式求值,a3+b3+c3?3abc= (a+b+c)(a2+b2+c2?ab?ac?bc)公式是化簡常用的手段.

A.3 B.2 C.1 D.0
變式1(數學競賽大考卷)已知a+b+c=1,a2+b2+ c2=2,a3+b3+c3=3,則ab(a+b)+bc(b+c)+ac(a+c)的值為( )

變式3(2005全國初中數學聯賽)已知a+b+c=0,a3+b3+c3=0,則a19+b19+c19等于( )
解:∵(a2+b2+c2)(a+b+c)=a3+b3+c3?3abc
又a+b+c=0,a3+b3+c3=0∴3abc=0,∴a,b,c至少有一個為0,若a=0,則b+c=0,b=?c,同理當b=0或c=0時a19+b19+c19=0.
[1]董永春,對幾個代數不等式研討的再探討[J].中學數學教學參考,2011(4).
[2]董永春,與高斯函數有關的高考壓軸題[J].數學通訊,2012(11-12).
[3]諸暨市浣江中學數學組[M].初中數學競賽大考卷,2005.

