理解三角形“四心”要“一意”,巧解習題勿“三心”又“二意”
廣州大學附屬中學(510050) 韓智明
理解三角形“四心”要“一意”,巧解習題勿“三心”又“二意”
廣州大學附屬中學(510050) 韓智明
從初中學習數學開始,學生就對三角形的“四心”(即:重心、垂心、外心、內心)有了初步的認識和理解.進入高中后,特別是學習向量知識以后,以向量為載體對三角形“四心”有關問題進行了深入的研究,大量的且不同形式的習題出現,沖擊著廣大師生的大腦.筆者從事高中數學教學多年,發現這塊知識學生很難把握,很多老師在平時的教學中雖然也有重點強調和講解,但感覺還是不夠系統,沒有從本質上揭示它們之間所蘊含的內在聯系,其實通過探究不難發現三角形的“四心”的向量表示有著統一的形式,本文就從三角形的“四心”向量統一表示形式及其相關結論入手,巧解一類與其有關的習題.
先看看一個引理的證明:




略解:由結論1、結論3和結論4可知,點G,N,P分別是△ABC的重心、外心和內心.故A正確.
點評:通過以上例題幾種解析方法發現,當知道和理解三角形“四心”向量統一形式后,利用結論來判斷,可以簡化解題步驟,達到事半功倍的效果.
下面以題組的形式舉例說明:
題1 已知A,B,C是平面上不共線三個點,動點P滿足
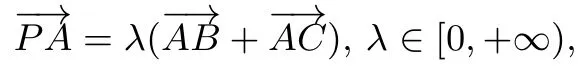
則P點的軌跡一定通過△ABC的( )
A.外心 B.內心 C.重心 D.垂心
題2 已知A,B,C是平面上不共線三個點,動點P滿足
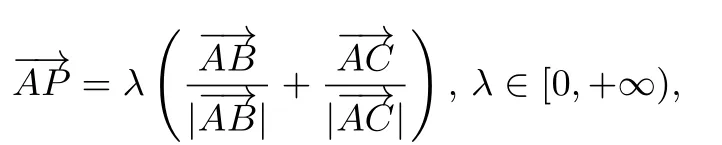
則P點的軌跡一定通過△ABC的( )
A.外心 B.內心 C.重心 D.垂心
題3已知A,B,C是平面上不共線三個點,動點P滿足
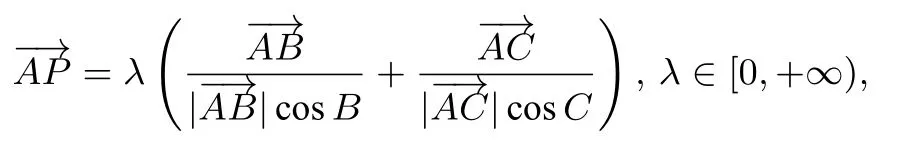
則P點的軌跡一定通過△ABC的( )
A.外心 B.內心 C.重心 D.垂心
題4 已知A,B,C是平面上不共線三個點,動點P滿足
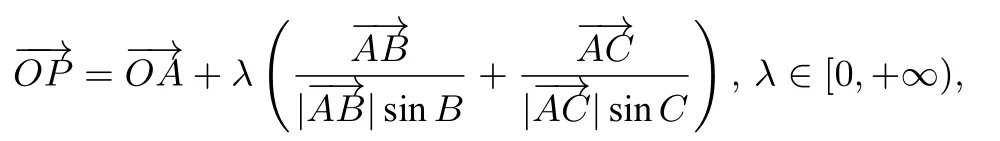
則P點的軌跡一定通過△ABC的( )
A.外心 B.內心 C.重心 D.垂心


以上題組1 3的解析方法,相信在學習中,很多師生都是這種解法,牢牢把握出題者的意圖,分析向量的幾何意義,結合選擇題的特殊性,不失為一種解題好策略,但縱觀這類題組,結合三角形“四心”向量的統一表示形式及其相關結論,我們可以嘗試更為深入地探究這一類題組的解法.


點評:通過題組1~4的另解發現,熟知三角形“四心”向量統一形式及其相關結論,我們可以更加深入地理解向量與三角形的內在聯系,充分挖掘習題中隱含的熟悉的結構模式,使得問題迎刃而解.
變式題組:
變式1已知A,B,C是平面上不共線三個點,若動點P滿足
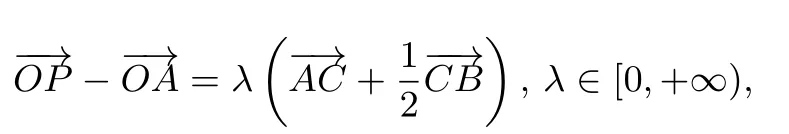
則直線AP一定過△ABC的( )
A.重心 B.垂心 C.外心 D.內心
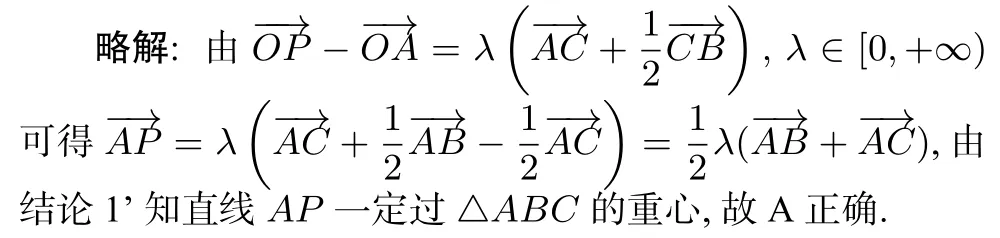
變式2已知A,B,C是平面內不共線三點,若動點P滿足
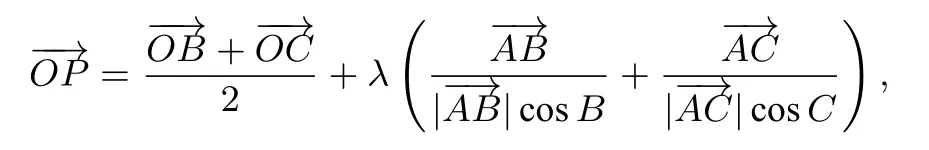
λ∈[0,+∞),則P點的軌跡一定通過△ABC的( )
A.重心 B.垂心 C.外心 D.內心
A.重心 B.垂心 C.外心 D.內心
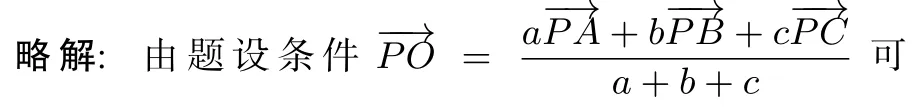

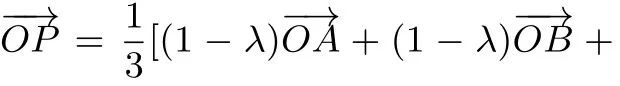
A.重心 B.垂心 C.外心 D.內心
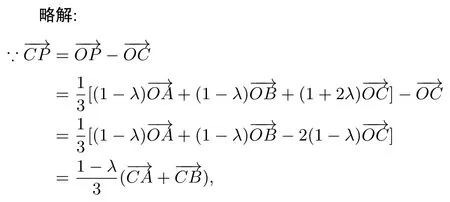
由結論1’知直線AP一定過△ABC的重心,故C正確.
點評:以上變式1~4對三角形“四心”的向量表示加以重組和改裝,終究還是改變不了向量的本質,仔細剖析還是可以轉化為三角形“四心”向量表示的統一形式,通過其統一形式及其相關結論進行巧解.
通過以上對三角形“四心”向量表示的統一形式及其相關變式結論的探究,結合題組和變式題組的解題方法的對比,我們對三角形“四心”向量表示的統一形式的認識就會更進一步加深,發現三角形“四心”問題在本質上其實就只有一種統一的向量形式,故在解決這一類習題時即對待三角形“四心”相關習題時,要觀察形式,探究本質,對比模式,形式上雖然是“四心”,究其本質就是“一意”.真可謂解決三角形“四心”要“一意”,巧解習題切勿“三心”又“二意”.
[1]吳時月.三角形“四心”的向量形式及其統一形式的再審視[J].中學數學研究,2015(12).
[2]汪華.三角形“四心”的向量統一形式[J].數學教育研究,2011(4).

